Espaces sémantiques et représentation du sens

Bernard Victorri

Introduction

Les nouvelles technologies de l’information sont en train de transformer profondément la recherche en linguistique. En effet, l’existence et la disponibilité de ressources électroniques de grande taille (très gros corpus, dictionnaires de toute sorte) permettent de développer des méthodes d’étude de la langue qui étaient encore impensables il y a dix ans.

En particulier, les méthodes statistiques, qui étaient reléguées à des traitements assez marginaux (analyse de fréquence lexicale dans des études de textes, par exemple), ont pris un nouvel essor. Leur rôle dans l’analyse syntaxique et sémantique des textes occupe une place de plus en plus importante (cf. par exemple, Habert et al. 1997, Habert et al. 1998).

Cela se comprend aisément : appliquées à des données massives et diversifiées, ces méthodes statistiques permettent d’étudier le fonctionnement de la langue « en vraie grandeur » : qu’il s’agisse de co-occurrences d’unité lexicales ou d’acceptabilité de constructions syntaxiques, le linguiste dispose de données en quantité quasiment illimitée, il peut construire des modèles basés sur l’analyse de ces données, et il peut tester les prédictions de ces modèles de manière objective et fiable. La linguistique contemporaine, qui a, un moment, cherché à atteindre l’idéal de scientificité que représente la physique théorique (cf. Milner 1989, Chomsky 1995) en devenant de plus en plus formelle, est en train d’acquérir un autre statut scientifique, plus expérimental et plus proche des sciences biologiques. Cette étape est sans doute nécessaire pour surmonter l’impasse dans laquelle s’étaient engagés un certain nombre de linguistes, plus attirés par l’élégance des constructions théoriques que par la dure, et parfois décevante, réalité des faits linguistiques, qui ne cessent de produire des contre-exemples aux effets dévastateurs pour ces tentatives de formalisation.

Notre travail s’inscrit dans ce nouveau courant en linguistique. En utilisant comme ressource électronique des dictionnaires de synonymes, nous avons cherché à mieux cerner l’organisation sémantique du lexique du français, et surtout à concevoir un mode de représentation du sens des unités lexicales (noms, verbes, adjectifs) qui prenne pleinement en compte la diversité des emplois de ces unités. C’est donc la polysémie, cette propriété si commune des mots de pouvoir prendre des sens différents suivant le contexte dans lequel on les utilise, qui est au cœur de ce travail.

Le phénomène de la polysémie

Il faut d’abord noter que la polysémie touche avant tout les mots les plus courants, ceux qui font partie du vocabulaire de base des locuteurs : il suffit d’ouvrir un dictionnaire pour s’en rendre compte. Plus un mot est utilisé dans le langage quotidien, plus il a de chances d’être polysémique. Qui plus est, ce phénomène est universel : il n’existe pas de langue humaine qui échappe à cette règle. Il ne s’agit donc pas d’un phénomène marginal, une sorte de « défaut » résiduel de langues imparfaites qui tendraient vers un idéal où tous les mots ne possèderaient plus qu’un seul sens. Au contraire, on doit considérer que c’est une qualité indispensable au bon fonctionnement du langage. Nous avons besoin de la polysémie pour pouvoir exprimer ce que nous avons à dire, et, pour notre appareil cognitif, la polysémie ne représente pas une difficulté supplémentaire à résoudre pour comprendre le sens d’un énoncé : c’est une caractéristique « normale » d’un énoncé, et les mécanismes cognitifs à l’œuvre dans la compréhension du langage traitent avec la même facilité les mots polysémiques et les mots monosémiques. Cette conclusion, surprenante au premier abord, peut être expliquée dans le cadre d’une conception dynamique de la construction du sens (Victorri 1996).

Pour qui s’intéresse au traitement automatique des langues, la polysémie constitue une difficulté considérable. En effet, lister tous les sens possibles d’un mot dans un lexique informatisé s’avère impraticable : d’abord parce que ces listes devraient être pratiquement infinies si l’on veut tenir compte de toutes les nuances qui peuvent colorer l’usage d’un mot, mais aussi et surtout parce que l’on perd par cette méthode ce que ces sens ont en commun, ce qui explique qu’ils puissent être portés par une même unité linguistique, ce qui fait au fond le « génie » de la langue qui a produit cette polysémie.

Prenons un exemple (tout à fait banal) : le mot peinture. Ce mot peut désigner le matériau utilisé pour peindre (ex : un pot de peinture), l’activité elle-même (ex : La peinture de la cuisine a pris 3 jours), le résultat de cette activité (La peinture de la cuisine est affreuse), une œuvre d’art (une peinture de Picasso), un type d’activité (la peinture en bâtiment), ou encore un type de description non picturale qui rappelle l’activité de peindre (la peinture des mœurs). Ces différentes significations doivent bien sûr être distinguées, et on pourrait les considérer comme autant d’entrées séparées dans un dictionnaire. Mais cela ne suffit pas si l’on veut une description précise des sens. Ainsi on s’accordera sans doute sur la nécessité de séparer les types d’activité, suivant que ce sont des activités industrielles ou artistiques (opposant ainsi la peinture impressionniste à la peinture en bâtiment). Jusqu’où doit-on aller ? Doit-on aussi différencier la peinture d’un immeuble de la peinture d’une voiture, qui utilise des procédés radicalement différents ? Et où doit-on placer la peinture murale, qui se situe à mi-chemin entre activité artistique et industrielle ? Que faire des peintures sur le corps humain, qui vont du maquillage et du vernis à ongle aux peintures rituelles de tout le corps pratiquées dans certaines sociétés ?

Un autre type de distinction s’impose dans le cas où peinture signifie ‘œuvre d’art’. On peut en effet parler de l’entité physique (Cette peinture est toute petite) ou du contenu (Cette peinture est très expressive). Il faut donc séparer aussi ces deux sens. Mais comment traiter alors les cas, nombreux, où les deux aspects sont évoqués simultanément (Cette petite peinture est un vrai chef d’œuvre) ? Doit-on différencier d’autres aspects, comme par exemple l’entité « commerciale » (Cette peinture est très chère) ?

On pourrait multiplier les exemples : il est clair que toute tentative d’élaboration d’une liste précise et consensuelle des sens d’un mot se heurte au fait que ces sens forment un continuum et non un ensemble discret, et qu’il y a donc une part d’arbitraire dans la manière dont on peut découper ce continuum. De plus, ce type de représentation occulte la question essentielle que nous avons évoquée ci-dessus : si un mot comme peinture devait être réduit à une telle liste de sens, l’usage de ce mot entraînerait une charge cognitive insupportable pour les locuteurs qui devraient, chaque fois que ce mot est employé, faire l’effort de découvrir quel sens de la liste on doit lui attribuer. Cela ne fonctionne visiblement pas comme cela. Le mot peinture possède un « potentiel sémantique » unique, qui permet à tout locuteur de construire dynamiquement le sens approprié dans un contexte donné sans avoir à parcourir mentalement la liste de ses différentes significations comme s’il s’agissait d’un mot d’une langue étrangère dont on rechercherait le sens pertinent en parcourant les différentes définitions qu’en donne un dictionnaire.

C’est pour cette raison que l’on se tourne de plus en plus vers d’autres modes de représentation d’une unité lexicale, mieux aptes à saisir le potentiel sémantique qui lui permet de déployer ses diverses significations. Au delà des divergences théoriques sur la conception du sens[1], les chercheurs en traitement automatique des langues partagent un objectif commun : obtenir des représentations qui permettent de calculer le sens d’un mot dans un contexte donné par des mécanismes généraux, et si possible « réalistes », c’est-à-dire compatibles avec ce que l’on sait aujourd’hui du fonctionnement cognitif de la compréhension du langage.

Dans notre laboratoire, nous avons conçu dans cet esprit un modèle de la polysémie (Victorri et Fuchs 1996), utilisant la théorie mathématique des systèmes dynamiques pour modéliser la construction du sens d’un énoncé. Dans ce modèle, on associe à toute unité polysémique un « espace sémantique », et le sens de l’unité dans un énoncé donné est représenté par une région de l’espace sémantique. C’est donc une approche continue du sens qui évite les difficultés engendrées par les représentations discrètes.

Espaces sémantiques

Pour illustrer la notion d’espace sémantique, reprenons l’exemple de peinture. Ses divers sens se distinguent par des valeurs différentes d’un certain nombre de paramètres, que l’on peut considérer comme autant de dimensions de l’espace que l’on va associer à ce mot. Ainsi on pourrait construire un espace quadridimensionnel permettant de représenter les variations des quatre paramètres suivants :

1. Un paramètre correspondant à la ‘nature du référent’, pouvant prendre les valeurs ‘matériau’, ‘activité’ et ‘résultat’. L’ordre dans lequel ces valeurs seront disposées sur la dimension correspondante est important : Il y a une plus grande proximité sémantique entre ‘matériau’ et ‘activité’ d’une part, et entre ‘activité’ et ‘résultat’ d’autre part. Il faut donc placer la valeur ‘activité’ au centre, pour respecter ces relations de voisinage topologique[2].

2. Un paramètre correspondant au ‘point de vue sur l’entité’, qui varie suivant que l’on évoque l’aspect ‘physique’, ‘commercial’ ou ‘signifiant’ de l’entité désignée par peinture. Là encore l’ordre est important, l’aspect commercial se situant naturellement entre les deux autres dans le continuum ainsi défini.

3. Un paramètre ‘domaine’ qui peut prendre les valeurs ‘industriel’, ‘artisanal’ et ‘artistique’, toujours en respectant une gradation sémantiquement motivée.

4. Enfin un paramètre ‘type de représentation’ qui permet de différencier l’activité picturale proprement dite des autres formes de description, langagières notamment, qui correspondent à des sens « figurés » de peinture (comme dans la peinture des mœurs).

Dans cet espace, le sens de peinture dans un énoncé donné peut être représenté avec précision par une région de l’espace : la région sera plus ou moins grande dans une dimension donnée suivant que le paramètre correspondant sera plus ou moins bien déterminé, et les sens intermédiaires trouveront leur place exacte dans le continuum de valeurs que peut prendre chaque paramètre. Cette représentation respecte les proximités de sens en les traduisant par des relations topologiques de voisinage et de recouvrement partiel entre les régions correspondantes de l’espace sémantique.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

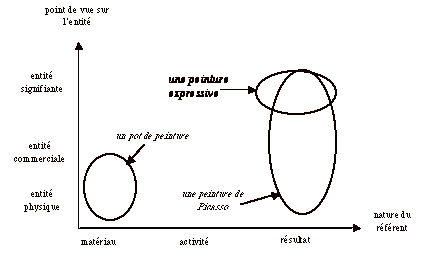
Figure 1 : Exemple d’espace sémantique

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Figure 2 : Représentation d’une ambiguïté alternative

 

 

Ainsi, si l’on se réfère à la figure 1, où l’on a représenté les deux premières dimensions de cet espace, on peut voir les régions associées à quelques unes des occurrences possibles de peinture. Comme on peut le constater, une peinture de Picasso, en l’absence de tout contexte plus précis, occupe une région qui couvre toute la dimension ‘point de vue sur l’entité’, puisque tous les aspects de l’entité sont a priori pertinents, alors que une peinture expressive est localisée plus précisément sur cet axe, puisque seule l’entité signifiante est évoquée par cette expression.

Bien entendu, la prise en compte de la troisième dimension conduirait à mieux localiser ces régions : ainsi un pot de peinture se situerait dans la partie ‘domaine industriel’ sur cette dimension alors que une peinture de Picasso occuperait la partie ‘domaine artistique’.

Il faut noter que cette représentation permet de aussi traiter les ambiguïtés alternatives comme un cas de figure spécifique, différent des cas de plus ou moins grande indétermination. Prenons l’exemple de la phrase : Pierre a acheté une belle peinture. En dehors de tout contexte, il peut s’agir d’un matériau ou d’un tableau. Dans ce cas, la région associée à peinture sera constituée de deux sous-régions séparées (« non connexes », en termes mathématiques) dans l’espace sémantique, comme on peut le voir figure 2.

Le logiciel Visusyn

Ce type de représentation rend donc mieux compte de la complexité des phénomènes de polysémie. Associer à chaque unité polysémique un espace sémantique plutôt qu’une liste de sens permet de déterminer avec précision le sens de chaque acception du terme étudié sans pour autant écarter la notion de proximité sémantique qui joue un rôle essentiel dans la définition même de la polysémie. De plus les différents « cas de figure » interprétatifs (sens précis, indétermination, ambiguïté alternative) correspondent à de véritables cas de figure géométriques dans l’espace associé, et c’est précisément sur cette base que l’on peut construire un modèle dynamique de construction du sens. Dans le modèle que nous avons conçu (cf. Victorri et Fuchs 1996), les régions correspondant au sens d’une unité dans un énoncé donné sont obtenues à partir des bassins d’attracteurs d’une dynamique dépendant des éléments contextuels présents dans cet énoncé. Ce modèle mathématique a été implémenté sur ordinateur à l’aide d’un réseau connexionniste fonctionnant par apprentissage, et nous avons pu montrer sur un exemple (le mot encore) que l’on pouvait ainsi calculer automatiquement le sens d’une unité polysémique dans n’importe quel énoncé qui la contient.

Mais l’application de cette méthode dans le traitement automatique des langues pose un problème redoutable. En effet, il faut, pour chaque unité polysémique de la langue, construire d’abord l’espace sémantique correspondant qui va être « codé » dans le réseau connexionniste. Comme on l’a vu avec l’exemple de peinture, ce travail de construction de l’espace ne présente pas de difficulté théorique particulière, mais il réclame une analyse linguistique spécifique pour chacune des unités lexicales de la langue. Etant donné le nombre des mots polysémiques d’une langue, il est irréaliste d’espérer pouvoir disposer d’une représentation de chacun de ces mots en un temps raisonnable.

C’est pourquoi nous avons cherché à automatiser ce processus en utilisant une ressource électronique : un dictionnaire électronique de synonymes du français[3]. Ce dictionnaire contient près de 50 000 entrées et 400 000 relations synonymiques. La base de départ est constituée de sept dictionnaires classiques (Bailly, Benac, Du Chazaud, Guizot, Lafaye, Larousse et Robert) dont ont été extraites les relations synonymiques qui ont été ensuite regroupées et homogénéisées. Les relations répertoriées dans ces dictionnaires sont des relations de synonymie partielle : pour que deux unités soient dites synonymes, il suffit qu’elles aient des sens très proches dans certains de leurs emplois, même si elles prennent des sens très différents dans d’autres contextes. Par exemple peinture et tableau, qui sont loin de partager tous leurs sens, sont considérés comme synonymes, parce qu’il existe des contextes où peinture peut être remplacé par tableau, et vice versa, sans changement notable de sens (c’est vrai aussi bien pour une peinture de Picasso que pour la peinture des mœurs).

Ainsi chaque synonyme ne couvre qu’une partie des emplois d’un mot donné et ne représente donc qu’une partie de l’espace sémantique que l’on cherche à construire. En revanche, si l’on considère l’ensemble des synonymes du mot, on doit obtenir un recouvrement de l’espace sémantique. Qui plus est, cet ensemble de synonymes est structuré, puisque l’on sait, pour chaque couple de synonymes du mot étudié, si ces deux unités sont elles-mêmes synonymes entre elles ou non. En termes mathématiques, on dispose de la structure du graphe constitué par la relation de synonymie. En particulier, on peut obtenir ce que l’on appelle les « cliques » du graphe, c’est-à-dire les sous-ensembles[4] de synonymes du mot qui sont tous synonymes entre eux deux à deux. Ce sont ces cliques qui vont nous permettre de construire l’espace sémantique.

Pour être concret, reprenons l’exemple de peinture. Le dictionnaire nous donne 52 synonymes, tels que couleur, barbouillage, fresque, croûte, toile, portrait, tableau, description, représentation, etc., qui couvrent assez bien tous les sens de peinture. Parmi eux, certains sont synonymes entre eux, comme toile et tableau, description et tableau, représentation et tableau, représentation et description, et d’autres ne le sont pas, comme toile et description, par exemple. Parmi les cliques du graphe, on aura donc au moins les deux cliques suivantes :

- peinture, tableau, toile.

- peinture, tableau, représentation, description[5].

Comme on peut le constater, ces deux cliques caractérisent deux sens précis de peinture : la première, le sens concret d’œuvre d’art picturale (une peinture de Picasso), et la deuxième, le sens plus abstrait de description non picturale (la peinture des mœurs). Si l’on calcule toutes les cliques du graphe de peinture, on obtient 49 cliques maximales, qui caractérisent chacune un sens précis de peinture. En voici quelques exemples supplémentaires :

- peinture, enduit, revêtement.

- peinture, badigeonnage, barbouillage.- peinture, barbouillage, croûte.- peinture, couleur, gouache.- peinture, couleur, fard.- peinture, aquarelle, gouache, image.etc.

Les cliques peuvent donc être considérées comme de toutes petites régions, que l’on peut assimiler à des points, de l’espace sémantique que l’on cherche à construire, puisqu’elles définissent des sens très étroits de l’unité polysémique étudié. En revanche, les synonymes occupent des régions beaucoup plus larges, puisqu’un même synonyme peut participer à de nombreuses cliques. En d’autres termes, la donnée d’un seul synonyme ne suffit pas à préciser suffisamment le sens (que l’on pense à tableau, par exemple), alors que la donnée d’une clique le permet.

Partant de ce constat, nous avons conçu un algorithme de construction de l’espace sémantique en définissant une distance entre cliques, considérées donc comme des points de l’espace à construire[6]. Cet espace comporte un grand nombre de dimensions, mais on peut obtenir, par des algorithmes classiques de décomposition en composantes principales, des visualisations assez fidèles sur un nombre réduit de dimensions. Nous avons réalisé un logiciel, Visusyn, qui permet d’effectuer l’ensemble de ces opérations. Ainsi, pour peinture, on peut voir figure 3 une projection bidimensionnelle de l’espace obtenu par Visusyn.

Comme on peut le constater, les cliques, représentées par des points, s’organisent suivant une certaine structure topologique : des points proches correspondent à des cliques de sens voisins. En première approximation, on peut estimer que ces points se situent le long d’une courbe, et que, si l’on parcourt cette courbe d’une extrémité à l’autre, on passe successivement par les sens ‘matériau’, ‘activité’, ‘œuvre d’art’ et ‘description’.

Sur la figure 4, on a représenté les régions correspondant à trois synonymes de peinture, choisis à titre d’exemple : barbouillage, portrait et tableau. Comme on pouvait s’y attendre, ces synonymes occupent des régions plus ou moins vastes de l’espace sémantique, suivant le degré de précision avec lequel ils spécifient le sens de peinture. On a aussi représenté deux sens largement sous-déterminés de peinture : une peinture chère (qui peut s’appliquer aussi bien au matériau qu’à une œuvre d’art) et une peinture expressive (qui peut s’appliquer à une œuvre d’art ou à une description non picturale).

Il faut noter que cette représentation est particulièrement économique : puisque l’on peut, en première approximation, considérer que l’espace sémantique se réduit à une courbe (variété à une dimension), cela veut dire que l’on peut représenter les principales variations de sens de peinture par un seul paramètre (l’abscisse curviligne sur cette courbe). Si l’on compare le résultat obtenu à l’analyse linguistique présentée à la section précédente, on remarque que la représentation automatique, tout en étant plus frustre, préserve une partie essentielle des distinctions que nous avions mises à jour. Cette représentation très simplifiée peut donc être suffisante pour de nombreuses applications en traitement automatique. De plus, si l’on a besoin de plus de finesse, rien d’empêche d’utiliser plus de dimensions, puisque, ne l’oublions pas, la représentation bidimensionnelle de la figure 3 n’est qu’une projection de l’espace sémantique multidimensionnel construit par le système.

Ainsi, on dispose d’une méthode informatique pour construire un espace sémantique associé à n’importe quelle unité polysémique de la langue. Même si les représentations ne sont pas parfaites, cette méthode, parce qu’elle est entièrement automatique, permet de concevoir des applications informatiques qui seraient inenvisageables sans cela. Cet outil peut aussi fournir une aide précieuse aux lexicographes et aux spécialistes de sémantique lexicale. En effet, comme nous allons le voir, l’examen de la structure de l’espace sémantique obtenu peut contribuer de manière significative à la compréhension de la polysémie d’un mot.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Figure 3 : Représentation des cliques de peinture

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Figure 4 : Représentation de quelques synonymes et sens de peinture

 

Un outil pour l’analyse linguistique

Pour illustrer l’intérêt de Visusyn pour l’analyse linguistique, nous avons choisi l’exemple du verbe jouer. Ce verbe est fortement polysémique, comme le montre les quelques exemples suivants :

Les enfants jouent dans la cour.

Pierre joue aux échecs.

Pierre joue en bourse.

Marie joue Andromaque.

Marie joue du piano.

Marie joue des coudes.

Pierre joue les innocents.

Pierre nous a joué un sale tour.

La porte joue sur ses gonds.

La barque joue sur son ancre.

etc.

Pourtant, au delà de cette diversité de sens, il semble bien que ce verbe présente une certaine unité sémantique, même si celle-ci n’est pas facile à définir. Comme le dit Pierre Cadiot dans la conclusion d’un article qu’il a consacré à ce verbe (Cadiot 1998) :

« Cette diversité de sens couplée à des propriétés formelles partiellement différenciantes pousse naturellement vers une vision dégroupante ou homonymique. Après tout, il peut paraître fort peu naturel de chercher à maintenir un sens commun à se jouer des obstacles et jouer les incompris, jouer à la marelle et jouer de malchance, jouer un cheval et jouer sur les nerfs de quelqu’un, etc. Les dégroupements des autres langues parlent aussi contre cette volonté de trouver à tout prix un sens commun. Pourtant, c’est bien notre intuition de locuteurs natifs qui nous pousse dans la voie inverse : celle d’un sens de base unique. Au delà de l’intuition, nous avons montré ici que la diversité des effets de sens était en corrélation avec des contraintes ou conditions externes systématiques. […]. Il reste à trouver un noyau stable de sens, une sorte d’instruction ou de schéma de base. »

Pierre Cadiot propose ensuite quelques pistes pour définir ce schéma de base. Nous les discuterons plus bas, mais auparavant, nous allons examiner les résultats fournis par Visusyn, pour montrer comment cet outil peut aider à analyser la structure polysémique d’une unité lexicale.

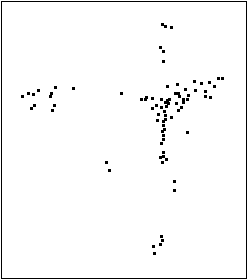
Le verbe jouer possède 94 synonymes dans notre dictionnaire électronique, et ces synonymes forment 98 cliques, ce qui correspond bien au haut degré de polysémie de ce verbe. On trouvera figure 5 la projection bidimensionnelle de l’espace sémantique construit par Visusyn. L’examen de la figure[7] permet de faire plusieurs observations intéressantes :

- On remarque d’abord qu’il n’y a pas de « dégroupement » notable des sens : on passe d’un sens à l’autre de manière continue, ce qui milite en faveur d’une unité sémantique de jouer, comme le propose Pierre Cadiot.

- Les diverses significations de jouer s’organisent selon deux axes (cf. figure 6). L’axe vertical fait passer progressivement de valeurs où jouer désigne une activité que l’on exerce aux dépens d’autrui (berner, duper, mystifier) à des valeurs où, au contraire, l’activité s’exerce à ses propres dépens (hasarder, risquer, miser). Sur l’axe horizontal, on passe de valeurs où l’activité est centrée sur le sujet (se divertir, rire, folâtrer) à des valeurs opposées où l’activité consiste à se projeter sur autrui (copier, imiter, simuler).

- Au centre de l’espace sémantique, on trouve des valeurs « neutres » pour les dimensions subjectives portées par les deux axes. C’est notamment dans cette zone que l’on trouve les sens de jouer dans lesquels il désigne une activité non intentionnelle (La porte joue sur ses gonds, La barque joue sur son ancre, etc.).

Cette dernière remarque peut nous permettre de découvrir ce qui fait l’unité du sémantisme de jouer. En effet, on peut faire l’hypothèse que ces valeurs neutres représentent un sens de base dont les traits essentiels seraient partagés par tous les sens du verbe. L’étude de ce sens de base peut donc se révéler très précieuse pour l’analyse sémantique du verbe.

Or dans ce type d’emplois, jouer désigne une activité qui s’exerce selon des degrés de liberté « non standards », non prévus par le dispositif en question. Une porte est faite pour tourner autour d’un axe. Quand elle joue sur ses gonds, cela signifie qu’à ce mouvement de rotation « normal » se superpose un mouvement non prévu de translation verticale qui représente une liberté supplémentaire pour le mécanisme.

Il est clair que cette caractéristique est présente dans tous les sens du verbe jouer. Dans tous les cas, jouer désigne une activité qui s’oppose à une activité régulière, programmée, en ouvrant des degrés de liberté sur lesquels cette nouvelle activité peut s’exercer. Cela ne veut pas dire que cette nouvelle activité ne soit pas elle-même régulée (que l’on joue aux échecs, au football, au théâtre, ou encore aux courses). Mais les règles de cette activité de jeu, quand elles existent, s’inscrivent dans un espace de liberté qui n’a plus rien à voir avec le fonctionnement de l’activité normale à laquelle elle s’oppose.

Il est remarquable que la définition que nous venons de donner pour jouer rejoigne pour l’essentiel les réflexions de Pierre Cadiot dans l’article que nous avons cité. En effet, au terme de son analyse, il propose de construire le schéma de base associé à jouer autour de deux notions de « dédoublement » et de « marge » :

« Le dédoublement semble une condition de base. Il faut que le jeu s’oppose à une activité présentée comme plus normale et régulière. […]. Une marge qui est une rupture dans la contrainte d’une programmation ou d’une attente, éprouvée surtout –mais pas seulement- dans sa dimension temporelle ».

Ainsi, cet exemple montre que les représentations obtenues par Visusyn sont pertinentes pour l’analyse sémantique de la polysémie. Bien entendu, ce n’est qu’un outil qui ne saurait se substituer au travail du linguiste. En particulier, il ne prend pas en compte le niveau syntaxique, dont l’importance est primordiale pour étudier le déploiement des sens d’une unité polysémique, comme le montre Pierre Cadiot dans son article. Mais c’est un outil puissant, qui fait clairement ressortir la structure sémantique d’une unité lexicale à partir des relations paradigmatiques que l’unité étudiée entretient avec les mots de sens voisins. A ce titre, il constitue une aide très précieuse pour les sémanticiens et les lexicographes.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Figure 5 : Espace sémantique associé à jouer

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

	agir aux dépens d’autrui

 

 

 

Figure 6 : Structure de l’espace sémantique associé à jouer

 

 

Conclusion

Comme on l’a vu, Visusyn permet d’obtenir des représentations des unités lexicales qui peuvent être exploitées aussi bien par les concepteurs de systèmes de traitement automatique du calcul du sens que par les linguistes spécialistes de la polysémie. Outre son intérêt pour les applications informatiques et la recherche linguistique, ce logiciel permet aussi aux simples usagers et amoureux de la langue de visualiser d’un seul coup d’œil le déploiement des sens d’un mot donné, et de saisir les principes qui régissent ce déploiement.

L’une des applications sans doute les plus prometteuses de ces techniques concerne le domaine de la traduction. En effet, on peut étendre la relation de synonymie interne à une langue à une relation entre langues, deux mots de langue différente étant considérés comme synonymes s’ils sont des traductions possibles l’un de l’autre. Si l’on dispose de dictionnaires de synonymes pour chacune des langues, ainsi que des dictionnaires bilingues correspondants, on peut donc, en utilisant les mêmes algorithmes, construire un espace sémantique pour un mot dans lequel ses traductions dans une langue cible occuperont des régions de l’espace. On obtient donc en outil d’aide à la traduction, qui présente visuellement une cartographie des sens d’un mot dans la langue source auxquels sont associées les traductions pertinentes dans la langue cible. Sabine Ploux a ainsi constitué ce qu’elle appelle des « atlas sémantiques » pour le français et l’anglais[8].

Ces travaux montrent tout l’intérêt de l’utilisation des nouvelles technologies dans le domaine de l’étude de la langue. Ce champ de recherche pluridisciplinaire, qui mobilise des mathématiciens, des informaticiens et des linguistes, est aujourd’hui en pleine expansion. En produisant de nouveaux outils d’appréhension et de maîtrise des phénomènes linguistiques, ces recherches vont sans aucun doute contribuer à transformer substantiellement notre relation à la langue et au texte.

Bibliographie

Cadiot P. (1998) : Les sens de jouer : esquisse d'une approche par le biais des attaches prépositionnelles, Prépositions et rection verbale, Presse Universitaire de Reims, 11:105-129.

Chomsky N. (1995) : Language and Nature,. Mind, 104 :1-61.

Habert B., Nazarenko A. et Salem A. (1997) : Les linguistiques de corpus. Paris, Armand Colin.

Habert B., Fabre C. et Issac F. (1998) : De l'écrit au numérique : constituer, normaliser, exploiter les corpus électroniques. Paris, InterÉditions.

Kleiber G. (1999) : Problèmes de sémantique – La polysémie en questions, Villeneuve d’Ascq, Septentrion.

Milner J.-C. (1989) : Introduction à une science du langage, Paris, Seuil.

Ploux S., Victorri B. (1998) : Construction d’espaces sémantiques à l’aide de dictionnaires de synonymes, Traitement automatique des langues, 39/1 :161-182.

Victorri B. (sous presse) : Langage et cognition : le malentendu cognitiviste, Des lois de la pensée au constructivisme, M.J. Durand Richard éd., Paris, Maison des Sciences de l’Homme.

Victorri B., Fuchs C. (1996) : La polysémie – Construction dynamique du sens, Paris, Hermès.