Programme de travail mamuphi (2008-2009) :
Théoriser le monde de la musique
à la lumière des mathématiques de Grothendieck (topos de
faisceaux)
et à l’ombre de la philosophie de Badiou (Logiques des
mondes)
François Nicolas
1. Stimuler
la théorisation de la musique à la lumière des « mathématiques
fondamentales » (A. Connes) contemporaines et, ce faisant, consolider une
ligne de partage des théorisations : pratiques théoriques musiciennes versus théories musicologiques [1].
Pour ce faire, après une pratique théorique convoquant la théorie mathématique
de l’intégration pour théoriser l’audition et l’écoute musicales [2],
une autre convoquant la diagrammatisation catégorielle pour théoriser le
concert et ses œuvres [3],
je voudrais, à la suite de la semaine Grothendieck [4],
convoquer la mathématique grothendieckienne des topos de faisceaux pour
théoriser le monde de la musique.
2. Déployer
cette pratique théorique de musicien à l’ombre de la philosophie, en
l’occurrence celle d’Alain Badiou (Logiques des mondes). [5]
3. Objectif
annexe plus pragmatique : s’approprier la mathématique en question (celle
des topos de faisceaux) en construisant un exemple systématique mettant à
l’épreuve la série des notions mathématiques qui s’y enchaînent. D’où, en cours
d’exposé, un certain nombre de remarques didactiques. On mesurera à cette
occasion combien ce « recours » musicien aux mathématiques s’écarte
méthodologiquement du rapport qu’un philosophe (tel Badiou) peut entretenir
avec la même mathématique. [6]
Soit le programme suivant :
1) Formaliser l’œuvre musicale comme faisceau [7] des interprétations de sa partition (I).
2) Formaliser la bibliothèque des partitions de musique comme site [8] de ses quodlibets (III).
3) Formaliser le monde de la musique comme catégorie [9] des morceaux de cette bibliothèque (V).
4) Formaliser ce monde de la musique comme topos [10] de ses morceaux [11] (VII).
5) Examiner les propriétés phénoméno-logiques du monde de la musique ainsi formalisé à l’ombre des concepts philosophiques de Logiques des mondes (IX).
6)
Boucler notre parcours en dégageant la part irréductible
d’ombre que la musique fait à la mathématique et que la philosophie
précisément, cette chouette de l’ombre plus encore de la lumière, sait le mieux
explorer (X).
Bien sûr on ne manquera pas d’examiner au fur et à mesure de cette pratique théorique (II, IV, VI, VIII) les propriétés onto-logiques qui en découlent pour notre monde de la musique et ses objets (les morceaux de musique).
Notations
5
I. Formalisation
(1) : l’œuvre comme faisceau
6
I.1 Cadre
général
6
I.2 Topologie
9
I.3 Foncteur
10
I.4 Préfaisceau
11
I.5 Faisceau
11
II. Premiers
résultats musicaux
11
II.1 Compte-pour-un
12
II.2 Un type singulier d’un
12
II.3 L’un d’un
faisceau : la situation locale comme constituante
12
II.4 Butée dans l’analogie
musique-mathématiques
13
III. Formalisation
(2) : la bibliothèque comme site
13
III.1 Cadre général
13
III.2 Topologie de Grothendieck
15
III.3 Site
17
IV. Seconds
résultats
17
IV.1 Importance de la
musicalisation incessante
17
IV.2 Importance du solfège
dans la musicalisation
17
IV.3 Frontière mobile
pièces/œuvres
17
IV.4 Importance musicienne
des quodlibets…
17
IV.5 Statut musical d’une
improvisation ?
17
V. Formalisation
(3) : le monde de la musique comme catégorie
18
V.1 Objets
18
V.2 Morphismes :
hypothèse fondamentale d’une formalisation sans interprétation 18
V.3 Morphismes
19
V.4 Limites/colimites
20
V.5 Objets
terminal/initial
21
V.6 Sous-objets
21
V.7 La catégorie Ⓜ est-elle « petite » ?
21
V.8 Foncteur représentable
21
V.9 Exponentiations
22
V.10 Catégorie de faisceaux
22
VI. Troisièmes
résultats
22
VI.1 Morceaux
« initiaux » et « terminaux » ?
22
VI.2 « Sous-morceaux » ?
22
VII. Formalisation
(4) : le monde de la musique comme topos
22
VII.1 Nouvelle hypothèse
fondamentale
23
VII.2 Nos faisceaux comme
Ω-ensembles complets
23
VIII. Quatrièmes
résultats
23
VIII.1 23
IX. Le
monde de la musique à l’ombre de la logique philosophique
24
IX.1 Être
& apparaître
24
IX.2 Minimum
et maximum : silence & ?
24
IX.3 Transcendantal
(classifieur de sous-objets) : solfège ?
24
IX.4 Conjonction
et enveloppe : rythme & timbre ?
24
IX.5 Dépendance
et envers : développement & altération ?
24
IX.6 Décision
matérialiste à l’endroit des Objets (Ω –ensembles)
24
IX.7 Composante
d’objet et atome : postulat du matérialisme
24
IX.8 Exposition
de la relation : (co)limite de (co)cône
24
IX.9 Foncteur
transcendantal
24
IX.10 Un
monde (topos)…
24
IX.11 …
et l’espace topologique de ses points
24
IX.12 Cardinalité
inaccessible ?
24
IX.13 L’œ(Œ)uvre-sujet ?
24
X. Suppléments
24
X.1 Yoneda
24
X.2 Rapport de notre
pratique théorique et la « théorie catégorielle »
24
Notations
P :
une partition
I :
une interprétation
E :
un enregistrement
S :
un sonagramme
℘ [={Pi}] : ensemble (dénombrable) de partitions
ℐ [={Ii}] : ensemble (dénombrable) d’interprétations
ℰ [={Ei}] : ensemble (dénombrable) d’enregistrements
S [={Si}] : ensemble (dénombrable) de sonagrammes
I(P) :
fonction interprétation I qui associe le sonagramme S à une partition P
ℐ(P) : Foncteur composé de la famille des fonctions I(P) pour une partition P donnée
ℱ(P) : ℱaisceau des interprétations I(P) pour une partition P donnée
Paramétrages
τ :
paramétrage horizontal [0, 1] d’une partition-rouleau P
t(τ) :
paramètre temporel d’une interprétation/enregistrement/sonagramme I/E/S
T :
durée globale d’une interprétation/enregistrement/sonagramme I/E/S
T° : τ→t = fonction « tempo »
Sonagrammes
ƒ(t) :
fréquence à l’instant t d’un sonagramme
S
a(ƒ,t)
ou aτ(ƒ) :
amplitude de la fréquence ƒ à l’instant
t d’un sonagramme S
α :
t→a(f) = fonction « amplitude »
i= αoT° : τ→a(f) = fonction « interprétation »
Topologie
sur une partition
μ[P(∆τ)] : moment de la partition P (délimité par l’intervalle ∆τ) = un « ouvert »
Q(P)=∑μi[P(∆τi)] : ouvert de P (composé comme pot-pourri tiré de P)
θ(P) : ensemble dans ouverts de P
Bibliothèque
K : catalogue du présite ℘
Q(℘)=∑μi(Pj) : ouvert de ℘ (quodlibet) = série des moments μi des partitions Pj
ℬ [=℘K] :
bibliothèque (structurée comme site) des partitions cataloguées selon K,
Ⓜ : topos des faisceaux ℱ(P)
sur ℬ , ou monde de la musique
Catégorie
M(Q) : morceau de musique (« objet » de Ⓜ) conçu comme faisceau sur la partition Q
m
ou m(M) : sous-objet de M (ou sous-morceau)
I.
Formalisation (1) : l’œuvre comme faisceau
Enjeu : formaliser qu’une œuvre est un faisceau
d’interprétations, le faisceau des interprétations d’une partition donnée.
Une interprétation sera alors une section (globale) de ce
faisceau [12].
I.1
Cadre général
Leitfaden
Il s’agit de formaliser les différentes interprétations
concevables d’une même partition donnée P.
On suppose ce faisant qu’il existe pour une œuvre donnée
(mettons la Fantaisie op. 17 de Schumann) un partition canonique.
Ces interprétations de P sont dénombrables : soit Ii(P) avec i∈ℕ.
On formalisera chaque interprétation via un enregistrement
E(I) puis un sonagramme S(E).
On fera les hypothèses (musicalement raisonnables) suivantes :
·
à 2 partitions différentes correspondent des
interprétations différentes : P≠P’ ⇒
I(P)≠I’(P’)
·
à 2 interprétations différentes correspondent 2
enregistrements différents : I≠I’ ⇒
E(I)≠E’(I’)
·
à 2 enregistrements différents correspondent 2
sonagrammes différents : E≠E’ ⇒
S(E)≠S’(E’)
·
donc, par transitivité, à 2 partitions différentes ne
peuvent correspondre que des sonagrammes différents : P≠P’ ⇒ S{E[I(P)]}≠ S’{E’[I’(P’)]}
Au total, on pourra donc discriminer les différentes
interprétations d’une même partition P directement par leur sonagramme.
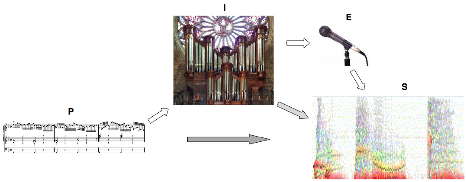
Éléments
Soit une partition P paramétrable horizontalement par τ∈ [0,1] : on donne donc à notre
partition la forme d’un rouleau d’un seul tenant, dévidable d’un bout à
l’autre. Le paramètre est musicalement mesuré : par exemple par le nombre
de mesures, de tactus ou d’impulsions élémentaires, ou encore par une distance
en centimètres sur l’édition de référence (on suppose bien sûr que la partition
canonique est dotée d’une édition de référence).
Soit une interprétation I de cette partition P, fixée par un
enregistrement E.
Cet enregistrement E peut se formaliser en un sonagramme S
qui indiquera, pour chaque fréquence ƒ de l’instant t, une amplitude a(t,ƒ), cette amplitude se trouvant généralement
représentée comme luminosité-couleur du point a.

Dans toute la suite (l’enjeu est ici une formalisation de
pensée, pas la mise en place d’un dispositif computationnel effectif !),
on supposera :
·
que l’enregistrement E n’influe pas sur la
compréhension de I, que E est techniquement neutre [13],
·
que le sonagramme S n’influe pas sur la compréhension
de E, que S est techniquement neutre [14],
·
qu’il y a donc bijection stricte entre ℐ={I} et S
={S} via ℰ={E} : ℐ≅ℰ≅S.
Par contre entre ℘={P}
et ℐ≅S ≅ ℰ,
il y a seulement surjection : pour tout P, existe au moins une I, un E et
un S.
On parlera donc indistinctement d’une interprétation I pour
désigner l’enregistrement E et/ou le sonagramme S.

L’interprétation I(P) peut se formaliser en S[I(P)] selon la
double application suivante :
·
elle établit une bijection (continue et
∞-différentiable [15])
entre τ∈[0,1] de la partition P et t∈[0,T] de l’interprétation I (où T
désigne le temps total de l’interprétation I) ; ceci formalise l’agogique
propre de l’interprétation en question (tempo, rubato, dimension temporelle du
phrasé…) ; appelons fonction tempo
cette fonction T° : τ→t ;
·
elle associe à tout instant t de l’interprétation I (i.e. à tout instant τ de la partition P) et à toute fréquence ƒ du sonagramme
S (ƒ∈ℝ+) une amplitude a(t,ƒ) – ce qui revient à dire
qu’elle associe à tout instant t (i.e. à
tout instant τ) une fonction (une
courbe de relief, par exemple) aτ(ƒ) de ℝ+
dans [0,1] [16] ; ceci
formalise le reste de l’interprétation (hauteurs-timbre-accords et
intensités…) ; appelons fonction amplitude cette fonction α : t→a(f).
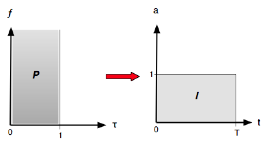
Soit la figure suivante :
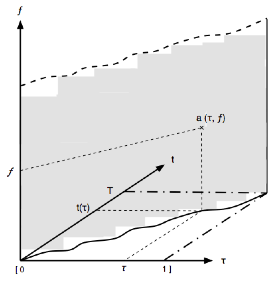
Le sonagramme S est ici représenté par un plan ondulé
vertical où chaque point sera coloré selon l’intensité de son amplitude. Autre
image : a désigne une
« altitude » - ici horizontale - du point sur le plan ondulé :
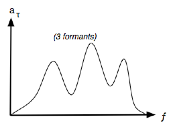
On peut référer directement a à τ plutôt qu’à t, soit a(τ,ƒ) – ou aτ(f) - puisque l’application τ→t est
bijective (en même temps qu’elle est continue et ∞-différentiable).
Appelons fonction interprétation cette fonction composée i= αoT° : τ→a(f).
Au total, on formalise une interprétation donnée I d’une
partition donnée P (paramétrée horizontalement par τ) par la donation d’un
sonagramme S c’est-à-dire la donation simultanée :
·
d’une fonction bijective tempo t(τ) de [0, 1] sur un intervalle de ℝ+,
·
d’une fonction amplitude α : t→a(ƒ) de [0, 1] sur l’ensemble des fonctions réelles
continues à valeur dans [0, 1].
On appellera I(P) [17]
la fonction résultante : P→S qui associe à tout couple (τ,ƒ) de réels
positifs le couple (t,a) de réels positifs :
I(P) : ℝ2→ℝ2
Plus précisément, la fonction I(P) fait correspondre à
l’espace constitué par la partie {[0,1]⊗[0,∞[}
de ℝ2 la partie {[0,T]⊗[0,1]} de ℝ2.
Remarque
L’ensemble ℐ (en
droit infini) des interprétations musicalement valides opère alors ainsi
(puisque T peut varier selon I) [18] :

puisque T dépend de I…
Point de méthode essentiel
On admettra ici que les musiciens disposent de la capacité
propre de trancher la validité ou non d’une I(P) donnée (c’est-à-dire d’un
sonagramme-enregistrement-interprétation donné pour une partition
donnée) : agogique valide (et donc durée T valide), exécution valide (en
termes d’accord des instruments, de vibrato, de taux de fausses notes musicalement
acceptables, et de dynamiques).
Rappel : la théorie mathématique des modèles suppose
bien que le modèle est doté d’une règle de véridicité immanente (non
formalisée : une sorte donc de boîte noire pour la théorie) apte à
trancher sur la valeur de vérité (vrai
ou faux) des formules du modèle.
Que la musique apparaisse pour partie aux mathématiques
comme une « boite noire » (boite noire à l’intérieur de laquelle les
musiciens, par contre, se meuvent en toute clarté) est essentiel : il ne
saurait y avoir de transparence intégrale de la musique pour la mathématique,
et ce pour des raisons philosophiques (la musique mobilise des sujets
singuliers - les œuvres et les Œuvres - ; or la mathématique ne peut
qu’ignorer le propre des sujets : tout au plus peut-elle radiographier
leur être et l’être de leurs effets [19]).
Il y a donc tout lieu de se « méfier » d’une
théorie mathématisée qui prétendrait formaliser un modèle musical dépourvu pour
elle d’obscurités, de consécutions incompréhensibles, de liaisons opaques…
I.2
Topologie
Revenons à une interprétation I donnée.
Les ouverts qui vont être au principe de la topologie de P
seront les intervalles de nature temporel : ∆τ désignera un intervalle
horizontal (de « temps ») sur la partition.
Remarque
On pourrait certes envisager de
compléter l’intervalle « temporel » par un intervalle vertical ∆ƒ (un
registre) de registres-fréquences. On aurait ainsi des parties-rectangles dans
la partition. Mais il n’est pas possible, dans le sonagramme, d’isoler un
intervalle de fréquences qui corresponde à un registre dans la partition :
les harmoniques des sons se mélangent, et c’est précisément en ceci réside que
l’interaction musicale. On ne peut donc associer fonctionnellement un registre
précis de la partition (un ∆hauteur) à
un formant du sonagramme (∆ƒ).
Il nous faut ainsi travailler fonctionnellement
sur les seuls intervalles « temporels » qui vont nous fournir la
topologie naturelle de P.
Ouvert de base : un moment
Si on dote ℝ de
sa topologie naturelle (un ouvert de base est un intervalle ouvert), alors
l’espace de départ P devient un espace topologique tel qu’un ouvert de base y
est un intervalle de temps (∆τ).
Convenons de noter μ[P(∆τ)] un moment de la partition P défini par l’intervalle ∆τ
On notera θ(P) l’ensemble des ouverts de P.
Une partie de P est donc, à la base, constituée d’un moment
particulier de la partition.
On compose à partir de là des ouverts par les axiomes topologiques traditionnels pour les ouverts (intersection finie – union ad libitum). Ceci nous conduit à bâtir dune famille de pots-pourris ou quodliberts ouverts.
Quodlibets…
La topologie d’une partition P s’édifie sur la base des intervalles ouverts ∆τ avec ∆τÌ[0,1] soit {∆τ}=P ([0,1]) – ensemble des parties de l’intervalle [0,1] -.
Un ouvert de P aura pour forme générale celle d’un ensemble de moments μ[P(∆τ)]. Appelons quodlibet un tel ensemble et notons-le Q(P). On écrira Q(P)=∑μ[P(∆τi)]=∑ μi
On retrouve ici cette vieille pratique musicale consistant à jouer des séries d’extraits d’une même œuvre, que ce soit pour des raisons didactiques ou pour des raisons de divertissement (songeons par exemple aux réminiscences, fantaisies, illustrations et paraphrases de telle ou telle œuvre chez Liszt).
Remarque
Un quodlibet étant défini par un ∑(∆τi) est un élément de P {P ([0,1])}.
Le nombre de quodlibets différents égale donc la cardinalité de P [P {P ([0,1])}]. Autant dire notre base de travail est formellement infiniment infinie !
Remarquons cependant que musicalement, les choses sont beaucoup plus restreintes : l’infinité est ici plus formelle que musicale s’il est vrai que toute partition ne disposant que d’un nombre fini d’éléments, l’ensemble des intervalles ∆τ musicalement différents est en vérité fini. D’où que le nombre de quodlibets musicalement différents restera lui-même fini (mais bien sûr extrêmement grand).
I.3
Foncteur
Rappelons : une interprétation I fait correspondre à
tout « point » de P (c’est-à-dire à tout instant τ) l’ensemble {tτ, aτ(ƒ)} d’un réel tτ et d’une
fonction continue réelle aτ(ƒ) :
ℝ→ℝ
À tout ouvert ∆τ de P, elle fera cette fois correspondre une
fonction t(τ) et une nouvelle fonction a(τ,ƒ) : ℝ2→ℝ.
Pour bâtir un foncteur, il nous faut ainsi passer d’une
fonction à une famille de fonctions et pour cela passer à l’espace de toutes
les interprétations.
On obtient ce faisant le Foncteur ℐ(P) des interprétations I (musicalement valides) de la même
partition P qui, à tout ouvert ∆τ de P (« moment » de P) associe
cette fois l’ensemble des fonctions (musicalement valides) {t(∆τ), a(τ,ƒ)}
Ce foncteur ℐ(P)
est clairement contravariant sur un ouvert de P : V→U ⇒F(U)→F(V)
où V→U (parfois noté V↪U) correspond à V⊂U.
C’est un foncteur contravariant de l’espace topologique θ(P) sur [une partie de] Ens (constituée par l’ensemble des
fonctions continues ℝ+→ℝ+). Appelons FCR ce dernier ensemble.
ℐ(P) : θ(P)op→Ens
ℐ(P)∈
Ensθop
ℐ(P) : θ(P)op→FCR⊂ Ens
Voyons maintenant comment ce foncteur ℐ(P) constitue un faisceau de fonctions
sur P à valeur dans Ens(FCR), faisceau qu’on notera ℱ(P).
I.4
Préfaisceau
De manière assez
immédiate, le foncteur ℐ(P) constitue un préfaisceau ℱ
car il satisfait la propriété de restriction : toute
réalisation sonore (sonagramme) valide d’une partie ouverte U de P constitue
bien par excès une réalisation sonore (sonagramme) valide de toute partie V de
U :
I(U) ∈ ℱ ⇒ I(V) = I|V
∈
ℱ
(on retrouve simplement là le caractère
contravariant de notre foncteur ℐ)
Rappel :
on note indifféremment ici I(U), E(U), S(U) puisque interprétations,
enregistrements et sonagrammes sont en correspondance bijective.
I.5
Faisceau
Ce préfaisceau ℱ
est en fait un faisceau car il satisfait
de plus la propriété de recollement : pour toute partie (ouverte) U de P et pour tout recouvrement (ouvert)
Ui de
U, si un ensemble d’interprétations Ii(Ui) est tel qu’elles
coïncident sur leurs parties communes, alors il existe bien (dans le faisceau ℱ) une et une seule interprétation I sur
U dont les restrictions coïncident avec les précédentes Ii sur les
différents Ui.
Rappels
Cette propriété de recollement sur un préfaisceau ne va pas
de soi : le point délicat tient ici [20]
non pas à l’existence en soi d’un unique « recollement » mais au
point de savoir si cet unique recollement – dont l’existence va de soi –
appartient bien au préfaisceau ℱ
des interprétations !
Cf. les contre-exemples élémentaires suivants :
·
Un préfaisceau de fonctions constantes n’est pas un
faisceau car une fonction « recollante » n’est plus une fonction
constante.
·
Le préfaisceau des fonctions continues bornées ℝ→U
n’est pas un faisceau car une fonction « recollante » n’est plus
bornée.
·
Soit un espace topologique T à deux points :
T={x,y}. Soit le préfaisceau ℱ
ainsi défini : ℱ(ø)=ø ; ℱ({x})=ℝ ;
ℱ({y})=ℝ ; ℱ({x,y})=ℝxℝxℝ. Une restriction est une projection. ℱ est clairement un préfaisceau. Or une
section globale sera déterminée par 3 nombres quand les valeurs des sections
sur {x} et {y} n’en déterminent que 2 : on ne peut donc recoller de
manière unique 2 sections sur {x} et {y}.
Sections
Une section du faisceau sur un moment U de P est une interprétation de ce moment.
Une section globale est une interprétation globale I-E-S de la partition P.
II.
Premiers résultats musicaux
On a donc établi qu’une œuvre est le faisceau ℱ(P) que composent les I(P). Une œuvre
musicale est un faisceau d’interprétations : une œuvre est le faisceau
des interprétations musicalement concevables d’une partition donnée.
Il est clair que cette démarche met au cœur de la pratique
musicale le rapport écriture-interprétations-perceptions [21].
Qu’est-ce que ce premier temps de cette pratique théorique
permet de clarifier musicalement ?
Quel est l’intérêt proprement musical de cette
formalisation ? Quel en est l’intérêt pour la musique ?
Rappel : on ne vise ici nulle implémentation
calculatoire de la formalisation. Cette formalisation vise à à éclairer
l’intellectualité musicale, à soutenir une Idée musicienne de la musique.
II.1
Compte-pour-un
Un premier intérêt de cette formalisation est de donner
forme à l’unité propre que constitue une
œuvre musicale : l’un d’une
œuvre musicale est ainsi formellement inscrit comme l’un d’un faisceau : le compte-pour-un de l’œuvre se
fait sous le paradigme du faisceau.
Ceci lève l’hésitation traditionnelle à établir où se joue
l’un d’une œuvre : est-ce dans
l’unité finie d’une partition (auquel cas on s’affronte au problème : où
est la musique si l’on s’arrête au niveau inaudible de la
partition ?) ? Et s’il n’y a de musique qu’audible, faut-il alors
compter pour un chaque nouvelle interprétation, poser donc qu’il y a non pas
« L’ »Appassionata mais
autant d’Appassionata différentes
qu’il y en a d’interprétations contrastées ?
Le compte-pour-un en terme de faisceau stabilise ainsi le
compte-pour-un de l’œuvre musicale.
II.2
Un type singulier d’un
Cette forme du compte-pour-un devient alors très précise
(cf. les propriétés constitutives des préfaisceaux et faisceaux) : il ne
s’agit pas seulement de compter-pour-un l’ensemble des interprétations. L’un d’une œuvre n’est pas seulement l’un d’un ensemble. Une œuvre n’est pas seulement l’ensemble
des interprétations musicalement recevables d’une partition donnée. Cet
ensemble est doté d’une structure particulière : celle de faisceau. C’est
un ensemble structuré.
C’est précisément cette structure de faisceau qui va nous
permettre dans la suite de construire des structures plus larges (en terme de
topos) qui sont mieux formées ou informées que de simples notions d’ensembles.
On ne se contentera pas de parler d’ensembles d’ensembles – ce qui ne spécifie
pas grand-chose s’il est vrai que l’Être général n’est fait que d’ensembles
d’ensembles ! – mais de faisceaux et de topos de faisceaux, ce qui nous
fera travailler sur des structures géométrico-algébriques précises. C’est
d’ailleurs ce qui nous permettra d’interpréter cette formalisation à l’ombre
cette fois de la philosophie de Badiou, d’une philosophie non seulement de
l’Être mais surtout – et ceci est forcément décisif pour la musique comme pour
tout art – des phénomènes propres à l’apparaître (à l’être-là).
II.3
L’un d’un faisceau : la situation locale comme
constituante
Un faisceau, c’est une manière de faire-un à partir du local
et « de proche en proche ».
Cette manière de faire-un nous intéresse musicalement car
elle est analogue au travail musical qui s’approprie toujours une partition de
proche en proche, de mesure en mesure, de page en page, de situation en
situation, et ceci vaut tout autant pour le travail musical d’exécution et
d’interprétation que pour le travail de l’écoute musicale (qui opère également
« de proche en proche ») et pour celui de composition. C’est aussi à
ce titre que la notion mathématique de faisceau est ici pour nous très
éclairante.
On comparera ainsi deux interprétations d’une même
partition [22] en priorité
par confrontation de passages avant de pouvoir confronter les grandes
architectures : ce qui légitimera que deux interprétations sont globalement
différentes sera toujours enraciné en des différences d’abord locales, ne
serait-ce que parce que l’écoute d’une interprétation donnée est toujours le
résultat d’un recollement de proche en proche : on ne saurait écouter
« d’un coup » une interprétation d’un bout à l’autre.
L’un du faisceau nous souligne que si une œuvre musicale
fait un, c’est avant tout parce qu’il
est musicalement légitime de confronter localement différentes interprétations
du même passage de la partition [23].
Et cela est légitime précisément parce qu’une œuvre n’existe réellement,
c’est-à-dire n’existe interprétée, que lorsqu’un musicien prend en charge (en y
prêtant un temps son corps, le temps de l’interprétation en question) cette
œuvre de proche en proche et non pas globalement : on sait combien
certaines supposées « visions globales » d’une œuvre peuvent rester
abstraites à mesure de ce qu’elles ne savent précisément pas se concrétiser
localement, « de proche en proche ».
Plus généralement, il n’y a de vrai travail musical, y
compris de composition, que « de proche en proche », ce qui n’est
nullement déconsidérer l’approche globale d’une partition [24]
mais simplement rappeler que cette globalité n’est ultimement jamais constituante :
elle est constituée par ce qui occupe en musique la vraie position constituante
et qui est la situation locale.
L’un d’une œuvre se constitue localement, et de proche en
proche, nullement globalement puis par restrictions locales successives.
Ainsi l’un de Tristan, ce n’est pas de
prime abord sa vaste architecture de quatre heures (au demeurant forme en arche
plutôt traditionnelle), c’est son début, étoilé du fameux accord qui rayonnera,
de proche en proche [25]
à grande échelle, c’est le renouvellement incessant de ces miniatures que
Nietzsche avait bien saisies comme le vrai constituant de l’art musical
wagnérien. Comme le moment-faveur de Farben, comme l’attaque de la première symphonie de Brahms,
comme la fin de l’opus 11 n°3 de Schoenberg, l’accord de Tristan est le germe local d’un faisceau de points de vue
musicaux à la fois différents et cependant localement enracinés en la même
micro-structure écrite. L’un d’une œuvre musicale procède bien d’un tel type de
variété contrôlé localement bien plus qu’assuré globalement.
II.4
Butée dans l’analogie musique-mathématiques
L’analogie musique-mathématiques peut être déployée selon le
principe suivant :
|
Musique |
Mathématique |
|
musicien |
mathématicien |
|
une œuvre |
un théorème |
|
un Grand Œuvre ou une configuration |
une théorie |
|
partition/interprétations |
démonstration/compréhensions |
mais elle bute alors sur le rapport
partition/interprétations : un théorème ne saurait être conçu comme le
faisceau des compréhensions auxquelles ouvre sa démonstration écrite. Il n’y a
pas d’équivalent mathématique strict à la série infinie d’interprétations
musicales ; d’où une historicité musicale sensiblement différente de
l’historicité mathématique…
Ceci souligne que le faisceau que nous avons construit pointe une singularité de la musique.
III. Formalisation (2) : la bibliothèque comme site
III.1
Cadre général
Nous avons vu comment une partition P engendre un ensemble
d’interprétations Ii,
et donc autant d’enregistrements Ei
et de sonagrammes Si :
P→IiEiSi et donc P→Si
où désigne un engendrement
unique
Remarque
ne désigne pas ici un monomorphisme car les I, E et S n’appartiennent pas à une même catégorie.
ne désigne pas non plus ici
un foncteur fidèle car les ensembles d’objets ℐ,
ℰ et S ne constituent pas, a priori, des
catégories (en tous les cas, on n’a pas ici défini de morphismes entre I, entre
E et entre S qui permettraient de structurer ℐ,
ℰ et S en catégories).
On a donc le diagramme suivant :
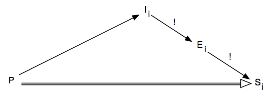
Demandons-nous maintenant, à l’inverse, dans quelles
conditions il est possible de remonter d’une interprétation I donnée ou d’un
enregistrement E donné à une partition P.
Transcriptions
Premier cas : exécution
On posera qu’il est toujours musicalement possible de
remonter d’une exécution musicale quelconque sur un instrument de musique
quelconque à la partition implicite de cette exécution et ce par ce qu’on appelle
musicalement une transcription. On
remarquera que les différents dispositifs « midi » réalisent désormais
automatiquement ce type de transcription.
On supposera qu’il est toujours musicalement possible de
compacter les différentes transcriptions envisageables selon une seule
partition canonique (face, par exemple, à différentes transcriptions du même
solo de Charlie Parker, on compactera ces différentes transcriptions en une
seule qui sera la plus détaillée).
On pose donc :
IP
Second cas : enregistrement sonore
On part ici d’un enregistrement sonore (par exemple d’un
chant d’oiseau).
On posera que certains de ces enregistrements sonores
peuvent être musicalisés au moyen d’une transcription qui prend musicalement
mesure de sa structure sonore.
On supposera, comme précédemment, qu’on aboutit pour ces
enregistrements (ceux que le musicien tient pour musicalisables), à une seule
partition-transcription canonique dans le cadre logique de l’écriture musicale,
disons du solfège (en entendant bien que ce solfège [26]
a une historicité propre et qu’il évolue au fur et à mesure, précisément, des
nouvelles tâches d’inscription musicale qu’il doit mettre en œuvre).
On pose donc :
EP
Remarque
On exclut ici toute écriture qui ne soit pas spécifiquement
musicale. Par exemple le codage informatique d’un enregistrement par une série
de 0 et de 1 stockés sur un CD n’appartient nullement à une telle écriture musicale.
Au demeurant, un tel type d’écriture n’ouvre à aucune réinterprétation du même
texte, en raison précisément du caractère non musical de ce texte informatique.
On a donc ici les flèches suivantes
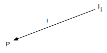
![]()
que l’on peut compléter alors des réinterprétations de la
partition-transcription obtenue (comme par exemple les Double Six ont pu le
faire pour quelques fameuses sessions de jazz…) dans le diagramme
suivant :

Une bibliothèque
On va sur cette base constituer une bibliothèque ℘
constituée de l’ensemble des partitions P existantes (ensemble dénombrable,
potentiellement infini).
Cette bibliothèque regroupe les partitions existantes de tous les morceaux (pièces [27] & œuvres) de musique, qu’ils aient été dès le départ musicalement écrits ou que leur écriture procède d’une transcription.
℘={Pi}
Présite
Comment géométriser cet espace ℘ de notre bibliothèque de partitions ?
Il nous suffit pour cela
1. de
disposer d’une mesure uniforme pour toutes nos partitions. On rappelle que
chaque partition a ici la forme d’un rouleau. Pour mesurer ces
partitions-rouleaux, on retiendra naturellement le paramétrage, identique pour
toute partition P, de son « temps » propre τ par l’intervalle [0, 1] : rapprocher
différentes partitions au point τ = 0,33 reviendra à les examiner toutes au
terme de leur premier tiers (spatialement mesuré)…
2. de
disposer d’un classement des partitions de notre bibliothèque, ce qui
formellement ne pose guère de problèmes puisque l’ensemble des partitions
constituant cette bibliothèque est dénombrable.
Au total, l’espace de notre bibliothèque est donc ainsi
formalisable :

Classement
Il faut ensuite choisir un ordre des partitions, sachant
qu’en ce point, l’expérience musicale n’en impose guère qui soit canonique. Il
y a donc, en ce point, un nouveau facteur subjectif qui va jouer : comment
tel ou tel musicien va-t-il classer cette bibliothèque de partitions ? Une
conséquence est qu’a priori, le topos des morceaux de musique auquel on va
aboutir sera construit légèrement différemment par chaque musicien. Mais en
vérité, tout ceci n’aura pas grande importance formelle (même si cette affaire de classement est par contre
musicalement décisive) puisque les différents espaces obtenus (en variant dans
la même bibliothèque l’ordre des partitions) s’avèrent formellement isomorphes
en sorte qu’on pourra facilement transiter entre bibliothèques ainsi
différemment ordonnées (toutes ces bibliothèques, différemment classées, étant
en tout état de cause composées des mêmes partitions, canoniquement éditées).
Remarque latérale : un fibré
Remarquons que notre bibliothèque est structurée comme un
espace fibré : elle est le produit d’espaces topologiques.
Chaque partition-rouleau, dotée de sa topologie canonique,
constitue une fibre P.
Notre axe vertical – catalogue dénombrable et ordonné -
constitue la base du fibré, laquelle va relever d’une topologie discrète. Soit
K le catalogue : K∈ℕ avec i∈[1,K]
qui indexe la partition Pi. On a ℘={Pi}.
Le pied de la fibre Pi
– ou projection sur la base K – est ici formalisé par le nombre i.
III.2
Topologie de Grothendieck
Pour constituer notre bibliothèque en site susceptible de
constituer la base d’un topos, il nous faut maintenant doter ce site d’une
topologie dite de Grothendieck.
Une telle topologie de Grothendieck vise à exprimer en termes catégoriels les propriétés des recouvrements topologiques en sorte de pouvoir doter une catégorie (faite d’objets et de morphismes, non d’ouverts et de fermés) de propriétés analogues à celles d’un espace topologique. En quelque sorte, il s’agit là de doter une catégorie d’un ersatz de topologie. Comme en fait notre bibliothèque est facilement topologisable, sa topologie naturelle va faire office de topologie de Grothendieck.
Mais rappelons d’abord le sens mathématique précis des notions ici nécessaires.
Principe général
Définition d’un recouvrement ouvert dans un
espace topologique
Soit les ouverts U de l’espace topologique T.
Un recouvrement ouvert associe à tout ouvert U de θ une
famille d’ouverts {Ux}
(où Ux⊂U) dite famille recouvrante C(U) telle que
1) U
appartient à cette famille C(U).
2) L’union
de recouvrants est un recouvrement de leur union.
3) La
restriction d’un recouvrant est un recouvrement de la restriction.
On a alors les propriétés suivantes [28] :
·
Cette famille C(U) inclut toute sous-famille qui
recouvre U de manière plus fine.
·
Cette famille C(U) recouvre également toute partie V⊂U.
·
Si une famille d’ouverts O(U) génère un recouvrement de
chaque partie Ux
du recouvrement C(U), alors cette famille O(U) est aussi un recouvrement de U.
Les ouverts de notre topologie (par intervalles horizontaux
dans les partitions) vont nous servir de base pour une telle topologie de
Grothendieck sur notre bibliothèque exhaustive de rouleaux ou de feuillets.
Définition d’une topologie de Grothendieck
Une topologie de Grothendieck transpose ces propriétés à une
catégorie [29] en
remplaçant espace topologique T par catégorie K, ouvert U par objet a, inclusion Ux⊂U
par morphisme ax→a, C(U)
par C(a), et nos trois propriétés
précédentes par celles-ci :
1. Ida : a→a∈C(a).
2. La
composition de deux recouvrants est un recouvrement du composé.
3. Le
produit d’un recouvrant est un recouvrement du produit.
Équivalences
Pour un espace topologique, un recouvrement topologique
équivaut à celui d’une topologie de Grothendieck [30].
On transforme en effet facilement un espace topologique en
une catégorie en transformant, à l’inverse de la transformation ci-dessus,
·
ses ouverts en objets de la catégorie ;
·
les inclusions ⊂
en morphismes ↪.
Il nous suffit donc de doter notre bibliothèque d’une
topologie et de recouvrements ouverts pour transformer cette topologie (au sens
traditionnel) en topologie de Grothendieck et par là transformer notre présite
en site.
Topologie naturelle
La topologie naturelle de la bibliothèque – espace fibré résultant – va être le produit de deux topologies, l’une horizontale (sur l’axe τ des partitions), l’autre verticale (sur l’axe - discret - du classement des partitions).
Des quodlibets
On a vu comment un ouvert d’une partition P était un quodlibet (série ordonnée de moments librement prélevés dans cette partition).
Étendons ceci à toute notre bibliothèque.
Un ouvert sera cette fois un quodlibet sur toutes les partitions Qi composant la bibliothèque (et non plus sur une seule).
On écrira Q(℘)=∑μi[Pj] : un ensemble de moments μi prélevés dans l’ensemble des partitions Pj.
Topologie discrète
Verticalement, la topologie de l’axe de classement des partitions sera la topologie discrète.
Rappel
Une topologie discrète compte tous ses éléments comme
ouverts en sorte que toute partie y devienne un ouvert. C’est la topologie qui
comporte le plus d’ouverts possibles.
Au total…
Au total, la topologie de ℘ sera le produit des deux topologies précédentes.
Qu’est-ce alors, dans cette bibliothèque, qu’un ouvert pour
cette topologie ? C’est un ensemble ad libitum de moments musicaux de longueurs arbitraires restant
indexés de la partition dont ils sont extraits.
Notation
La bibliothèque ℘={Pi} munie de cette topologie sera notée ℬ (pour ℬibliothèque).
III.3 Site
Recouvrements
La notion classique de recouvrement ouvert d’un espace
topologique [31]
suffit à constituer les recouvrements de nos ouverts de ℬ.
Notre topologie « naturelle » sur ℬ suffit donc à doter notre bibliothèque d’une topologie de Grothendieck et donc à constituer notre présite en site.
IV.
Seconds résultats
Examinons les nouveaux « résultats » de cette
« pratique théorique ».
Qu’est-ce que la constitution de notre bibliothèque musicale
en « site » nous apprend musicalement ?
IV.1
Importance de la musicalisation incessante
Cf. vie de la bibliothèque par incorporation incessante de
nouvelles transcriptions et de nouvelles manières de transcrire. Cf.
déplacement incessant des frontières du monde-Musique pour y incorporer de nouveaux types de sonorités,
d’instruments, etc.
N’oublions pas non plus les territoires musicaux laissés en
jachère puis abandonnés par la musique vivante (voir certains instruments -
luth, orgue, … - et certains genres – parmi les différentes danses par exemple
-). Une musique n’existe vraiment que rejouée : les enregistrements du
passé sont des images de musique plutôt que de la musique vivante… Ce sont des
photos de la musique du passé plutôt qu’une musique d’ici et maintenant.
IV.2
Importance du solfège dans la musicalisation
Cf. les enjeux proprement logiques de l’écriture musicale.
Cf. les transformations et mutations de l’écriture musicale…
Cf. enjeu aujourd’hui : comment musicaliser l’écriture
informatique ?
IV.3 Frontière mobile pièces/œuvres
Cette différence (interne au monde-Musique et non plus externe comme les précédentes) est
subjective : on peut donc incorporer à un nouveau processus sujet (à une
nouvelle subjectivation) - on peut musicalement subjectiver - ce qui jusque-là
n’était qu’une simple pièce.
Réciproquement, une œuvre de musique peut être jouée,
exécutée comme une simple pièce et être ainsi désubjectivée, réduite à un
simple morceau de concours, numéro virtuose, pièce du répertoire, etc.
IV.4 Importance musicienne des quodlibets…
Cf. appropriation de la musique comme monde sous forme de
libres et variés quodlibets, propres à chaque musicien (ex. séries de
moments-faveur, de « beaux passages », de « classiques
favoris »,…).
IV.5
Statut musical d’une improvisation ?
Qu’en est-il du statut musical précis d’une improvisation
non enregistrée ?
C’est une chose musicale morte, qui a vécu seulement le
temps de son exécution, qui peut laisser des souvenirs dans la tête des
musiciens (des individus) mais qui, pour le monde-Musique, est morte. Pour le monde-Musique, cette chose a le simple statut d’une étincelle.
Le monde-Musique
qu’on vise ici à formaliser inclut bien ce genre d’étincelles. Il faut donc
tenir non pas exactement que ce monde est un topos (comme si tout ce qui n’avait pas le statut d’un faisceau –
telle ou telle improvisation non enregistrée par exemple – ne pouvait y
appartenir) mais qu’il a la structure d’un topos de faisceaux.
V. Formalisation
(3) : le monde de la musique comme catégorie
Nous avons successivement montré :
1) que
l’œuvre musicale est le faisceau des interprétations de sa partition ;
2) que
la bibliothèque des partitions de musique est le site de ses quodlibets.
La catégorie des faisceaux d’interprétations sur ce site va constituer un topos de Grothendieck [32].
On appellera Ⓜ le topos des faisceaux ℱ(P) sur ℬ et on posera que ce topos Ⓜ des morceaux de musique formalise « le monde de la musique », c’est-à-dire que le monde-Musique a la structure d’un topos de ses morceaux.
Voyons d’abord (V.1) ce que veut dire que notre ensemble de faisceaux sur notre site ℬ forme une catégorie.
Nous verrons ensuite (V.2) ce que veut dire que cette catégorie forme un topos.
Remarque
Où l’on éprouve l’intension effective de cette pratique théorique : le développement mathématique des notions mobilisées pousse en avant notre formalisation d’un monde-Musique et par là notre exploration musicienne de ses propriétés…
Pour transformer notre ensemble de faisceaux sur un site en
catégorie, il faut doter cet ensemble de propriétés particulières, et pour
commencer il va nous falloir indiquer ce que vont être, dans cette catégorie,
les morphismes entre objets-faisceaux.
V.1
Objets
Nos objets sont nos faisceaux, c’est-à-dire les faisceaux
d’interprétations d’un quodlibet (ou d’une œuvre) donné.
Notation
Notons désormais M (pour « morceau de musique »)
un tel faisceau en tant qu’objet de Ⓜ.
On distinguera soigneusement le faisceau M de sa base scripturale Q qui désigne la partition du quodlibet prélevé dans la bibliothèque ℬ.
M signifiera donc M(Q), soit le faisceau des interprétations
de la partition (construite plus qu’héritée) Q(uodlibet).
V.2
Morphismes : hypothèse fondamentale d’une
formalisation sans interprétation
Qu’est-ce qu’un morphisme entre de tels faisceaux :
M→M’ ?
C’est un rapport entre deux faisceaux, donc pour nous entre
deux « morceaux ».
Quels rapports musicaux allons-nous ici prendre en
compte ? La décision est d’importance : une catégorie est mathématiquement
définie tout autant par ses morphismes que par ses objets - ainsi un même ensemble
d’objets peut donner lieu à des catégories fort différentes selon les relations
(entre ces objets) qui vont les structurer -.
Nous allons décider de ne pas formaliser ici nos morphismes
(nos rapports entre « morceaux » de musique) comme nous avons
formalisé nos objets (nos « morceaux de musique, comme faisceaux de leurs
interprétations).
Nous allons poser que ces rapports sont les rapports
musicaux que les musiciens pratiquent et connaissent par leur travail propre
d’interprétation et d’analyse musicales : ce sont les rapports entre
pièces et œuvres musicales qui sont pointés lorsque les musiciens parlent de
l’influence de telle œuvre sur telle autre, de l’esprit différent/proche qui
anime telle et telle, de la Forme-Sonate (ou Fugue, ou Rondo, etc.) commune entre
telle et telle, etc.
Le principe, somme toute, est le suivant : si notre
formalisation opère comme la théorisation d’un modèle (au sens de ce qu’on
appelle en logique « la théorie des modèles »), il est d’essence de
cette théorisation que le modèle soit sans morphismes (sans
« déduction »), l’enjeu de la théorisation étant précisément de doter
les formalisations d’objets de déductions propres à l’espace théorique ainsi
constitué.
Notre pratique théorique revient en effet à bâtir une
théorisation toposique du monde de la musique (ou monde-Musique) qu’on peut diagrammatiser ainsi :
On posera donc que M→M’ ne formalise pas, à proprement
parler, tel ou tel rapport prédéfini entre morceaux mais que ce morphisme est
une donnée propre à notre espace théorique.
On ne posera même pas qu’il convient d’interpréter dans
notre modèle (monde-Musique) ce
morphisme en terme de relation musicale entre morceaux car si, dans le cadre de
« la théorie des modèles » il y a bien lieu par principe
d’interpréter les objets, il n’y a nullement lieu par principe d’interpréter
les morphismes ! Tout au plus pourra-t-on se demander – ce que nous ne
cessons de faire et qui constitue bien l’intension propre de cette pratique théorique – comment tel ou
tel objet déduit dans notre espace théorique peut–être interprété dans notre
modèle (le monde-Musique).
Précision : la face « théorie » de la pratique théorique
Ceci nous conduit à préciser notre vocabulaire.
Si l’on peut légitimement appeler « théorie » la
face formalisée de notre travail, comme on peut légitimement appeler
« modèle » la face ici empiriquement constituée de notre monde de la
musique, l’ensemble du mouvement (la dialectique formalisation/interprétation
entre les versants musicaux et mathématiquement formalisés) continue bien de
relever de ce qu’on a proposé d’appeler une pratique théorique du musicien.
Précision : Ⓜ ≠ monde-Musique
Distinguons pour cela soigneusement notre modèle (le monde
de la musique qu’on propose de doter d’un nom propre en le renommant monde-Musique) de sa formalisation en topos de faisceaux Ⓜ. Le monde-Musique est notre modèle et Ⓜ désigne la formalisation de
ce monde-Musique en topos. Ⓜ n’est donc
pas le monde-Musique ! À proprement
parler, il n’est pas non plus sa structure. Il faut plutôt dire que Ⓜ est la
formalisation théorique (mathématisée) de la structure du monde-Musique ; en plus ramassé : Ⓜ est la
structure formalisée (mathématisée) du monde-Musique.

Et il n’y a pas d’interprétation « naturelle » des
morphismes de Ⓜ
dans le monde-Musique :

Il nous faut donc poursuivre notre élaboration théorique en
dotant notre ensemble Ⓜ
des morphismes adéquats à le constituer d’abord en catégorie, puis en topos
sans nous soucier d’interpréter ces morphismes dans notre monde-Musique.
V.3
Morphismes
On adoptera bien sûr la figure canonique des morphismes
entre faisceaux, qui nous assure dans un premier temps l’existence de
morphismes identité pour chaque faisceau, la composition et l’associativité des
morphismes (propriétés nécessaires à la constitution de catégories).
Rappelons simplement les autres caractérisations
catégorielles concernant les morphismes.
Monomorphismes/épimorphismes/isomorphismes
Il s’agit de la généralisation des
injection/surjection/bijection traditionnelles.
|
Injection : f(a)=f(b)⇒a=b a≠b⇒f(a)≠f(b) |
Injection
catégorielle :
ƒog=ƒoh
⇒ g=h |
Monomorphisme (conserve les différences) ƒog=ƒoh
⇒ g=h
simplifiable à
gauche |
|
Surjection : ∀b $a:f(a)=b |
Surjection
catégorielle :
∀g $h:ƒoh=g |
Épimorphisme (préserve les identités) goƒ=hoƒ
⇒ g=h
simplifiable à
droite |
|
Bijection : a=bÛf(a)=f(b) a≠bÛf(a)≠f(b) |
|
Isomorphisme goƒ=Id(a) / ƒog=Id(b)
|
V.4
Limites/colimites
Limites à gauche / Colimites à droite
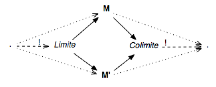
Exemples de Limites / colimites :
a. Produits/sommes
Les produits (MxM’) et sommes (M+M’) :
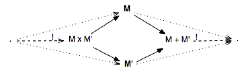
Produit de faisceaux
On définit le produit de M et M’ par les couples
suivants : [MxM’](Q)=M(Q)xM’(Q)
b. Égalisateurs/coégalisateurs
Les limites et colimites du diagramme à deux flèches
f°e=g°e… / c°f=c°g…
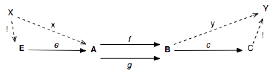
c. Produits fibrés [33]
/ sommes amalgamées [34]

V.5
Objets terminal/initial
Objet terminal 1
Généralisation du singleton : M1
Faisceau terminal
1 est donné par 1(Q)={Ø} soit un singleton.
Objet initial 0
Généralisation de l’ensemble vide Ø : 0M
Faisceau initial
V.6 Sous-objets
Un sous-objet m de M est une classe d’équivalence
dans les monomorphismes de cible M (↣M) :
ceux qui sont équivalents au monomorphisme m : ↣M
Sous-faisceau
Un sous-faisceau A d’un faisceau F (ou « parte »
de F) est tel que pour tout Q, A(Q)⊆F(Q).
V.7
La catégorie Ⓜ
est-elle « petite » ?
Oui, car nous travaillons ici constamment dans des ensembles
bien délimités : chaque partition de notre bibliothèque comporte un nombre
entier de signes et notre bibliothèque comporte un nombre entier de partitions.
Chaque partition ouvre à un nombre entier d’interprétations.
L’extension progressive de notre espace de travail se fait
donc par construction progressive à partir de ℕ
en sorte qu’on reste donc à tout moment dans un cadre ensembliste de pensée.
V.8
Foncteur représentable
C’est un cas particulier des Foncteurs de Ⓜ dans Ens. [35]
Une topologie pour laquelle chaque foncteur représentable
est un faisceau est appelé standard. [36]
Rappel
Cf. à tout M de Ⓜ on associera deux foncteurs Ⓜ[M,-]covariant
et Ⓜ[-,M] contravariant de Ⓜ dans Ens que je note plus simplement ℳ- et ℳ- :Ⓜ→Ens
Par exemple, pour le premier ℳ-=Ⓜ[M,-]
· ℳ-(M’)={M→M} : un objet M donne un ensemble de
morphismes ;
· ℳ-(f :
M’→M”)={ℳ-(M’)→ℳ-(M”)}={g:{M→M’}→{M→M”}} avec g=f°u
(un morphisme entre objets donne un ensemble de morphismes entre deux ensembles
de morphismes).
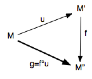
On dit que M représente
ces deux foncteurs.
Inversement, un foncteur F : Ⓜ→Ens (co/contra-variant) sera dit représentable s’il existe M tel que F soit
naturellement équivalent à Ⓜ[M,-] ou Ⓜ[-,M].
V.9 Exponentiations
V.10 Catégorie de faisceaux
On a ainsi décrit la catégorie de nos faisceaux qui se
trouve être de plus dotée des principales propriétés supplémentaires aptes à la
constituer en topos. Ce point n’est bien sûr pas une surprise : c’est tout
au contraire la conséquence escomptée du fait d’avoir formalisé nos morceaux de
musique comme objets-faisceaux.
VI.
Troisièmes résultats
Qu’est-ce qu’un monde-Musique ainsi structuré en catégorie ?
Selon notre hypothèse fondamentale d’une formalisation sans interprétation des morphismes, il nous faut seulement examiner ce qu’il en est d’une interprétation musicale des objets nouvellement dégagés.
Il s’agit essentiellement
1) des objets initiaux et terminaux 0 et 1,
2) des sous-objets (sous-faisceaux) d’un objet (faisceau) donné.
À quels types de morceau de musique ces différents objets correspondent-ils ?
VI.1 Morceaux « initiaux » et « terminaux » ?
VI.2
« Sous-morceaux » ?
VII. Formalisation (4) : le monde de la musique comme topos
Étant une catégorie de
faisceaux (soit un type tout à fait particulier de catégorie), notre
catégorie est un topos de Grothendieck et donc aussi (théorème de Giraud) un
topos élémentaire (au sens cette fois de Lawvere).
On sait [37] en effet que la théorie des topos résulte de
la confluence de deux problématiques : celle de Grothendieck (topos de
faisceaux), celle – plus logique - de Lawvere. La première [38] a précédé la seconde [39], et le théorème de Giraud [40] est venu relier les deux.
Pour notre pratique
théorique de musicien, on ne va pas s’engager ici dans une trop vaste
récollection des propriétés différenciées de ces deux sortes de topos (même
s’ils se recouvrent en bonne part). On se contentera pour ce faire de renvoyer
à la bibliographie existante et on examinera seulement ici les propriétés
susceptibles de nous éclairer dans notre démarche particulière.
Quelles sont les
propriétés d’un tel topos qui vont nous intéresser ici ?
VII.1 Nouvelle hypothèse fondamentale
Pour les besoins propres de cette pratique théorique, il
nous faut revenir sur nos objets (les faisceaux qui formalisent nos morceaux de
musique) en sorte de mieux examiner comment les morphismes entre ces objets
(ces morphismes que nous n’avons pas à interpréter musicalement) éclairent nos
objets, ont prise sur eux.
L’idée est la suivante : vu catégoriellement, un
morphisme éclaire le « contenu » d’un objet (c’est le cas déjà pour
les sous-objets mentionnés plus haut) au point même qu’il soit possible (voir
plus loin le lemme de Yoneda) de dire que les morphismes « éclatent »
l’objet qu’ils prennent pour origine et pour cible (au sens où l’on parle en
dessin industriel de l’éclaté d’un moteur).
Il nous faut donc réexaminer nos faisceaux-morceaux sous un
nouvel angle mathématique en sorte de voir comment ces mêmes objets, rééclairés
comme Ω-ensembles complets, vont donner lieu à un ensemble de morphismes apte à
constituer un topos.
Argument
Ce nouvel éclairage des objets de base de Ⓜ et donc de ces entités de
base de notre monde-Musique que
constituent nos morceaux est légitimé par une autre visée stratégique de cette
pratique théorique : la déployer à l’ombre de la philosophie de Logiques
des mondes. En effet, la constitution
d’objets (au sens cette fois philosophique du terme), d’objets d’un monde
donné, est au principe de cet ouvrage (rappelons qu’il procède à une triple
opération : il disjoint radicalement l’objet du sujet et vise versa, il
refonde sur cette base un concept philosophique de l’objet séparé de toute
problématique subjective, et il refonde sur cette base élargie un concept
philosophique du sujet qui n’a nullement pour ressort un rapport à quelque
objet que ce soit). Et ces objets ont précisément pour support onto-logique ces
Ω-ensembles complets.
Formaliser nos objets-faisceaux en tels Ω-ensembles complets
nous mettra donc sur la piste « naturelle » d’une interprétation
cette fois philosophique de nos morceaux de musique comme « objets »
du monde-Musique (objet entendu cette
fois au sens philosophique de Logiques des mondes).
Récapitulatif : les hypothèses fondamentales de notre formalisation
Si l’on récapitule notre parcours, notre pratique théorique
s’est déployée sous quatre hypothèses fondamentales successives en matière de
formalisation :
1) formaliser l’œuvre musicale comme faisceau de ses interprétations ;
2) formaliser la bibliothèque de musique comme site des partitions de quodlibets ;
3) ne pas interpréter musicalement les morphismes de notre théorie mathématique comme on en interprète par contre les objets ;
4) formaliser nos faisceaux comme Ω-ensembles complets en prenant en charge l’interprétation musicale de cette nouvelle vision mathématique de nos objets.
*
Voyons comment nos faisceaux peuvent être structurés en Ω-ensembles
complets (Goldblatt 388) en sorte de construire un topos Ⓜ comme catégorie de
faisceaux sur une algèbre de Heyting complète (Goldblatt 408)…
VII.2
Nos faisceaux comme Ω-ensembles complets
Évaluation des ressemblances/différences entre deux éléments
d’un même faisceau (i.e. entre deux interprétations
d’une même partition) par indexation sur Ω=[0,1] : R(I-I’)∈[0,1], avec
R(I,I’)= R(Iτ-I’τ)dτ
VIII.
Quatrièmes résultats
Qu’est-ce qu’un morceau de musique vu comme Ω-ensemble complet ?
Qu’est-ce qu’un monde de la musique structuré comme topos de ce type de morceaux ?
VIII.1
IX. Le
monde de la musique à l’ombre de la logique philosophique
Cf. interprétation selon les concepts philosophiques de Logiques des mondes. Qu’en est-il des propriétés phénoméno-logiques d’un monde des morceaux de musique ?
IX.1 Être
& apparaître
L’interprétation comme apparaître de l’être-partition du morceau de musique ?
IX.2 Minimum
et maximum : silence & ?
IX.3 Transcendantal
(classifieur de sous-objets) : solfège ?
IX.4 Conjonction
et enveloppe : rythme & timbre ?
IX.5 Dépendance
et envers : développement & altération ?
IX.6 Décision
matérialiste à l’endroit des Objets (Ω –ensembles)
IX.7 Composante
d’objet et atome : postulat du matérialisme
IX.8 Exposition
de la relation : (co)limite de (co)cône
IX.9 Foncteur
transcendantal
IX.10 Un monde (topos)…
IX.11 … et l’espace
topologique de ses points
IX.12 Cardinalité
inaccessible ?
IX.13 L’œ(Œ)uvre-sujet ?
X. Suppléments
X.1 Yoneda
Discussion critique de la présentation de Yoneda par Mazzola
Résultats musicaux
X.2
Rapport de notre pratique théorique et la « théorie
catégorielle »
« Théroie catégorielle » ? Cf. la troisième
notion du titre de Barr & Wells : Topos, Triples and Theories : il y s’agit
d’interpréter une théorie mathématique comme la constitution simultanée d’une
catégorie (notre catégorie théorique Ⓜ)
et d’un foncteur sur cette catégorie (notre « interprétation ») qui
génère une nouvelle catégorie de structure analogue (ici notre monde-Musique), en l’occurrence celle de topos.
L’enjeu va être ici d’examiner en quoi cette compréhension
logico-mathématique du champ complet (et pas seulement du versant formalisé) de
notre pratique théorique de musicien peut certes l’éclairer mais surtout peut
dégager la part essentielle de cette pratique théorique qui reste ici
mathématiquement dans l’ombre. Ainsi cette part irréductible d’ombre que la
musique fait à la mathématique est précisément celle que la philosophie,
chouette de l’ombre plus encore de la lumière, sait le mieux explorer pour
son propre compte.
Retour sur ce qui distingue cette pratique théorique musicienne de la
théorie mathématique de Mazzola
Il s’agit donc de tracer ici une ligne de partage aussi
précise que possible d’avec une prétention mathématicienne à l’hégémonie qui
consisterait à rendre compte mathématiquement des rapports institués par cette
pratique théorique musicienne entre musique et mathématiques. Il s’agit donc
ici de revenir sur l’hypothèse de Mazzola d’une pure et simple adjonction entre
théorie mathématique et modèle musical pour en montrer l’ineffectivité
proprement mathématique et pour en dégager donc le substrat moins philosophique
que proprement mythologique.
Où l’on va retrouver cet antique partage : à quel ombre
disposer son activité théorique, celle de la philosophie ou celle du mythe ?