http://patrick.saintjean.free.fr/Teratec2020.html
http://patrick.saintjean.free.fr/
http://patrick.saintjean.free.fr/ChoixBibliographiquePSJ.html
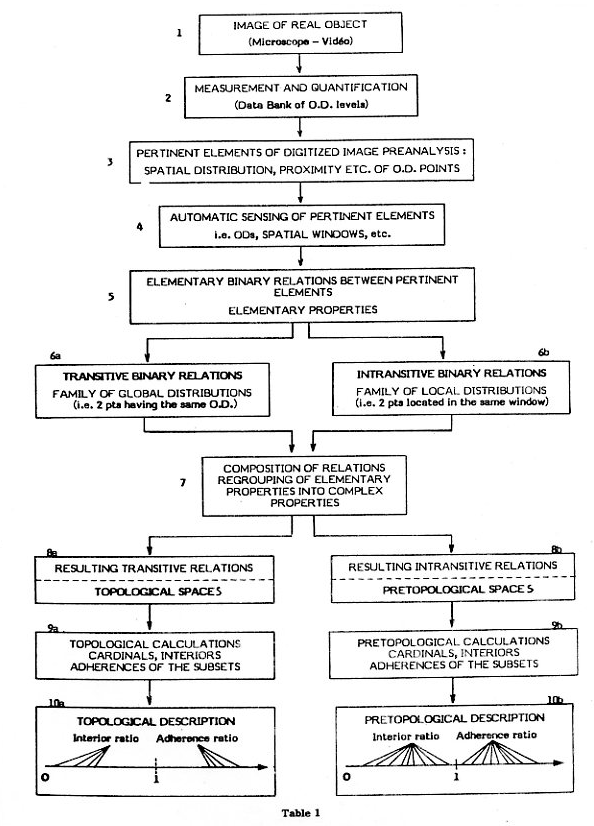
Studio Virtuel Interactif en Réseau
appliqué au Génie Biologique et Médical
GBM-LAB
Runing@Home à la Française
pour Chercheurs isolés ou Groupes de R&D à distance voulant travailler ensemble
Studio Visio-Conférence interactive, inter-créative et inter-créactive en
Réseau de Bibliothèques de Fonctions informatiques auto et inter-structurantes
connectables à distance pour former une structure fonctionnelle,
avec visualisation et contrôle interactif de structure
(mots opérateur, mots opérande, structure spatiale d'entrées,
structure spatiale d'opérations, structure spatiale de sorties,
structure de liens et de connectivité, structure temporel et de synchronisation)
de l'instruction informatique arithmétiques, logique, graphique
et chorégraphique à structure opérationnelle
pour l'observation (temps réel et/ou différé), la captation, le prétraitement et le traitement des données
ainsi que la synthèse pour restructuration, représentation, et expression des données.
Ainsi chaque chercheur peut créer, modifier, exécuter, contrôler, et corriger
un graphe fonctionnel à partir de toutes les fonctions du réseau
en respectant les entrées-sorties et bénéficiant des expressions numériques, graphique et textuelle.
Travaux en cours
Il est utile de bien connaître l'existant qui fonctionne (FOLDING@HOME, ROSETTA@HOME avec BOINC)
et d'en apprécier son utilité, son efficacité et ses manques,
pour à la fois converger vers des connexions possibles et développer une version innovatrice à la française.
GBM-LAB avec le FOLDING@HOME
In 2020, International Citizen Scientists create an Exascale Computer to Combat COVID-19
https://foldingathome.org/papers-results/
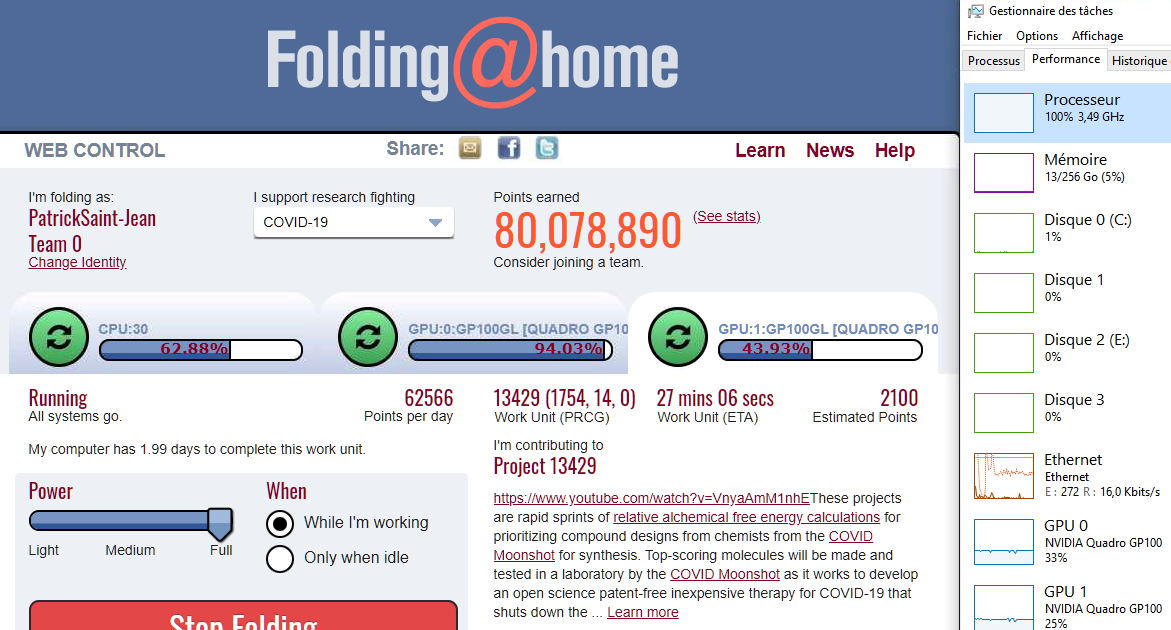
As contributor of Folding@home, Patrick Saint-Jean is folding to support researches fighting COVID-19
with more than 80,000,000 points earned from April to November 2020 and
Contributing to 6 International Groups of Researche :
- Sweden : KTH /SciLifeLab Delemotte Lab
https://www.biophysics.se/index.php/members/sergio-perez-conesa/
https://www.biophysics.se/index.php/projects/delemottelab/
Simulation of a potassium ion channel inactivation and conduction.
Potassium ion channels are crucial proteins of the membranes of excitable cells like neurons or cardiac cells.
They open and close based on stimuli allowing for the conduction of ions (in essence electric impulse) through the membrane.
Their malfunction is related to diseases such as cardiac arrhythmias or epilepsy.
The first COVID19 project from our lab consiste of assembling the envelope protein, which is an ion channel important for viral function.
Learning about how it forms can inform the design of molecules that will prevent proper assembly.
- Washington University School of Medicine in St. Louis : Greg Bowman's lab
https://bowmanlab.biochem.wustl.edu/software/
Sukrit Singh is a Biophysics PhD student
This project simulates the SARS-Cov2 nsp12 polymerase (RNA-directed RNA polymerase),
which is responsible for duplicating the SARS-Cov2 genome during infection.
These simulations will focus on identifying druggable pockets on the protein's surface as well as predicting the effect of mutations on drug sensitivity.
Artur is a Graduate Student
This project simulates several myosins found in the human body.
Myosins are the proteins responsible for most of the force generated by the body, from the contraction of muscles to the movement of materials around the cell.
Understanding the mechanistic basis of drugs that might be used to treat defects in myosin, including hypertrophic and dilated cardiomyopathies as well as heart failure.
Myosin was featured as the PDB Molecule of the Month in June 2001.
- Temple University, Department of Chemistry, Philadelphia, Pennsylvania, United States : The Voelz Lab
participates in the Folding@home project, hosting two servers.
Dr. Voelz was formerly a postdoctoral scholar in the Vijay Pande lab at Stanford University.
http://voelzlab.org
Neha is a postdoc.
Coronavirus SARS-CoV-2 (COVID-19 causing virus) proteins.
These are high-priority projects to simulate the proteins of the COVID-19.
Dylan Novack is PhD student.
https://foldingathome.org/2020/03/10/covid19-update/
https://foldingathome.org/news/
COVID Moonshot designs : https://covid.postera.ai/covid
Fragment HITS from DIAMOND
14676 - FEP screening of 20 fragment hits from DIAMOND UK in solution
14333 - SARS-CoV-2 RBD domain in complex with human neutralizing S230 antibody Fab fragment (PDBs: 6nb8, 2ghv)
http://dx.doi.org/10.1016/j.cell.2018.12.028
SARS-CoV-2 COVID Moonshot absolute free energy calculations generated on
Folding@home now released as an AWS Open Data Set by Vincent Voelz, November 2, 2020
- Hong Kong University of Science and Technology : Huang Lab
http://compbio.ust.hk/public_html/pmwiki-2.2.8/pmwiki.php?n=Main.HomePage
developing and applying novel computational tools which bridge the gap between experiments and simulations.
Examples of the interested research areas include RNA folding, protein misfolding/aggregration,
conformational changes in Transcription Elongation, and the development of Markov State Models for long timescale dynamics.
a hub for Folding@Home in Asia
- University of Illinois at Urbana-Champaign : the Shukla Group
https://shuklagroup.org/
to combine theory, computation, and experiments to develop quantitative models of biological phenomena relevant for health, energy, and climate change.
The research program is focused on developing a platform for understanding regulation of protein function
such as elucidating mechanistic insights to regulate plant growth and development in context of global climate change.
This system is the solvated human ACE2 (Angiotension-converting enzyme 2) and the RBD (receptor-binding domain) complex involved in SARS-CoV-2 transfection.
These simulations will allow us to understand the major interactions responsible for binding of these proteins and how the protein behave in the body.
- MSKC, Memorial Sloan Kettering Cancer Center, New York, USA : John Chodera Lab
Computational and Systems Biology Program, Sloan Kettering Institute, https://www.mskcc.org/research/ski/labs/john-chodera
The Projects 17505-08, Disease Type: cancer, are high-temperature vanilla simulation of an apo kinase AURKA : N-MYC complex to explore protein-protein interactions.
https://foldingathome.org/2020/07/28/introducing-covid-moonshot-weekly-sprints-help-us-discover-a-new-therapy/
https://www.youtube.com/watch?v=VnyaAmM1nhEThese projects are rapid sprints of relative alchemical free energy calculations
for prioritizing compound designs from chemists from the COVID Moonshot for synthesis.
Top-scoring molecules will be made and tested in a laboratory by the COVID Moonshot as it works to develop
an open science patent-free inexpensive therapy for COVID-19 that shuts down the essential SARS-CoV-2 main viral protease.
The COVID Moonshot has already made and tested hundreds of compounds, and is pursuing several good lead series.
You can see their progress in real time here: https://covid.postera.ai/covid/submissions/compounds
In addition to helping us prioritize compounds,
you can help purchase more compounds for synthesis at cost from Enamine
by sponsoring the GoFundMe page for patent-free open science COVID-19 drug discovery!
This is a radical new approach to drug discovery that aims to rapidly produce inexpensive new therapies.
This project is managed by at Memorial Sloan Kettering Cancer Center.
http://choderalab.org
The Chodera lab combines expertise in theory, computation, and automated biophysical experiments
to transform physics-based simulations into predictive models
of drug binding, dynamics, and selectivity for the design of anticancer therapeutics.
https://www.biophysics.se/index.php/members/sergio-perez-conesa/
https://www.biophysics.se/index.php/projects/delemottelab/
Simulation of a potassium ion channel inactivation and conduction.
Potassium ion channels are crucial proteins of the membranes of excitable cells like neurons or cardiac cells.
They open and close based on stimuli allowing for the conduction of ions (in essence electric impulse) through the membrane.
Their malfunction is related to diseases such as cardiac arrhythmias or epilepsy.
The first COVID19 project from our lab consiste of assembling the envelope protein, which is an ion channel important for viral function.
Learning about how it forms can inform the design of molecules that will prevent proper assembly.
- Washington University School of Medicine in St. Louis : Greg Bowman's lab
https://bowmanlab.biochem.wustl.edu/software/
Sukrit Singh is a Biophysics PhD student
This project simulates the SARS-Cov2 nsp12 polymerase (RNA-directed RNA polymerase),
which is responsible for duplicating the SARS-Cov2 genome during infection.
These simulations will focus on identifying druggable pockets on the protein's surface as well as predicting the effect of mutations on drug sensitivity.
Artur is a Graduate Student
This project simulates several myosins found in the human body.
Myosins are the proteins responsible for most of the force generated by the body, from the contraction of muscles to the movement of materials around the cell.
Understanding the mechanistic basis of drugs that might be used to treat defects in myosin, including hypertrophic and dilated cardiomyopathies as well as heart failure.
Myosin was featured as the PDB Molecule of the Month in June 2001.
- Temple University, Department of Chemistry, Philadelphia, Pennsylvania, United States : The Voelz Lab
participates in the Folding@home project, hosting two servers.
Dr. Voelz was formerly a postdoctoral scholar in the Vijay Pande lab at Stanford University.
http://voelzlab.org
Neha is a postdoc.
Coronavirus SARS-CoV-2 (COVID-19 causing virus) proteins.
These are high-priority projects to simulate the proteins of the COVID-19.
Dylan Novack is PhD student.
https://foldingathome.org/2020/03/10/covid19-update/
https://foldingathome.org/news/
COVID Moonshot designs : https://covid.postera.ai/covid
Fragment HITS from DIAMOND
14676 - FEP screening of 20 fragment hits from DIAMOND UK in solution
14333 - SARS-CoV-2 RBD domain in complex with human neutralizing S230 antibody Fab fragment (PDBs: 6nb8, 2ghv)
http://dx.doi.org/10.1016/j.cell.2018.12.028
SARS-CoV-2 COVID Moonshot absolute free energy calculations generated on
Folding@home now released as an AWS Open Data Set by Vincent Voelz, November 2, 2020
- Hong Kong University of Science and Technology : Huang Lab
http://compbio.ust.hk/public_html/pmwiki-2.2.8/pmwiki.php?n=Main.HomePage
developing and applying novel computational tools which bridge the gap between experiments and simulations.
Examples of the interested research areas include RNA folding, protein misfolding/aggregration,
conformational changes in Transcription Elongation, and the development of Markov State Models for long timescale dynamics.
a hub for Folding@Home in Asia
- University of Illinois at Urbana-Champaign : the Shukla Group
https://shuklagroup.org/
to combine theory, computation, and experiments to develop quantitative models of biological phenomena relevant for health, energy, and climate change.
The research program is focused on developing a platform for understanding regulation of protein function
such as elucidating mechanistic insights to regulate plant growth and development in context of global climate change.
This system is the solvated human ACE2 (Angiotension-converting enzyme 2) and the RBD (receptor-binding domain) complex involved in SARS-CoV-2 transfection.
These simulations will allow us to understand the major interactions responsible for binding of these proteins and how the protein behave in the body.
- MSKC, Memorial Sloan Kettering Cancer Center, New York, USA : John Chodera Lab
Computational and Systems Biology Program, Sloan Kettering Institute, https://www.mskcc.org/research/ski/labs/john-chodera
The Projects 17505-08, Disease Type: cancer, are high-temperature vanilla simulation of an apo kinase AURKA : N-MYC complex to explore protein-protein interactions.
https://foldingathome.org/2020/07/28/introducing-covid-moonshot-weekly-sprints-help-us-discover-a-new-therapy/
https://www.youtube.com/watch?v=VnyaAmM1nhEThese projects are rapid sprints of relative alchemical free energy calculations
for prioritizing compound designs from chemists from the COVID Moonshot for synthesis.
Top-scoring molecules will be made and tested in a laboratory by the COVID Moonshot as it works to develop
an open science patent-free inexpensive therapy for COVID-19 that shuts down the essential SARS-CoV-2 main viral protease.
The COVID Moonshot has already made and tested hundreds of compounds, and is pursuing several good lead series.
You can see their progress in real time here: https://covid.postera.ai/covid/submissions/compounds
In addition to helping us prioritize compounds,
you can help purchase more compounds for synthesis at cost from Enamine
by sponsoring the GoFundMe page for patent-free open science COVID-19 drug discovery!
This is a radical new approach to drug discovery that aims to rapidly produce inexpensive new therapies.
This project is managed by at Memorial Sloan Kettering Cancer Center.
http://choderalab.org
The Chodera lab combines expertise in theory, computation, and automated biophysical experiments
to transform physics-based simulations into predictive models
of drug binding, dynamics, and selectivity for the design of anticancer therapeutics.



Atelier de 3D Printing (Impression 3D additive et soustractive)
Covid-19 connected to ACE2 and spike glycoproteine on the capside of covid connected to T4 (3D Printing, Resine AnyCubic),
Visière Z-Glass Zortrax 3D printing (M300, with printing of Covid-Paravent from Geneviève Bonieux)
https://www.arsmathematica.org/IS/index-IS.html
Engagé dans la lutte contre la Covid19 et tout autre virus dangereux pour la survie humaine
- on met de côté l'utilisation du virus comme vecteur de thérapie -
l'approche du Design artistique s'exprime dans la vision 3D virtuelle, où formes et couleurs prennent tout leur sens
pour imager, faire imaginer et simuler mentalement une réalité micro et nanoscopique à la fois structurelle, fonctionnelle et dynamique.
Dans son Design, l'entité biologique macromoléculaire prend toute sa beauté intrigante
dans sa forme et sa plasticité à s'interactivé entre-elles (amines, protéines, enzymes) et le long des structures plus complexes (hélice, ADN, ARN, génome).
L'impression 3D peut en rendre compte dans son esthétique et une forme de Poïétique de la création,
mais également dans l'approche du Design Scientifique
où l'interaction automatique, conversationnelle et interactive avec l'expérimentateur (UX-Design) peut se faire invisio (par la virtualité numérique)
mais également par le concret d'un jeu de construction biomoléculaire comme celui de Zoom-Tools pour les atomes.
Ici les biomolécules constituent les entités premières, entières et déformables selon leurs propriétés
mais aussi s'interconnectant selon leurs liaisons et relations chimiques et leurs formes évolutives
se déplaçant sur les structures, s'agrégeant ou se dispersant, se découpant et se recollant ailleurs pour se dupliquer ou se répliquer, voire se muter.
Ce Bio-Design Tools serait très utile aux expérimentateurs mais également pour la formation des biochimistes et des enfants prodiges, ou pas,
et peut être un passage concret-abstrait-virtuel par le concret à l'analyse et traitement virtuels sur ordinateur et écran interactif.
Les R&D en Génie Biologique et Médical du CREDACI GBM-LAB reprend les travaux des années 1974-89
(Robotique de Laboratoire pour la culture cellulaire et l'imagerie biomédicale 2D et 3D) de façon plus théorique,
mais avec une volonté de simulation dynamique et interactive 3D des Capteurs de Virus Thérapeutiques
pour compenser la saturation et soulager les systèmes immunitaire et respiratoire, en assurant le prétraitement des virus après stockage pour être retraités naturellement.
En effet, nous savons que "the air transports viruses and other pathogens. Since viruses are smaller than other bioaerosols, they have the potential to travel further distances. In one simulation, a virus and a fungal spore were simultaneously released from the top of a building; the spore traveled only 150 meters while the virus traveled almost 200,000 horizontal kilometers." "Aerosols (<5 μm) containing SARS-CoV-1 and SARS-CoV-2 were generated by an atomizer and fed into a Goldberg drum to create an aerosolized environment. The inoculum yielded cycle thresholds between 20 and 22, similar to those observed in human upper and lower respiratory tract samples. SARS-CoV-2 remained viable in aerosols for 3 hours, with a decrease in infection titre similar to SARS-CoV-1. The half-life of both viruses in aerosols was 1.1 to 1.2 hours on average.
The results suggest that the transmission of both viruses by aerosols is plausible, as they can remain viable and infectious in suspended aerosols for hours and on surfaces for up to days."
Ainsi faire des capteurs de virus passe par la culture de bioaérosols de type cellulaire et l'expérimention virale en Robomate de Culture.
Cellules suffisamment petites de grosses bactéries pouvant attirer le virus à l'intérieur pour être traité
à des fins de destruction et/ou d'inaction et de phagisme passif.
Après pulvérisation dans les poumons ou inhalation ou projection dans l'environnement
les virus captés ne peuvent plus nuire immédiatement, directement et indirectement.
Reste à récupérer les capteurs de virus par expectorations et crachats dans des mouchoirs jetables, par pompage,
et pour l'environnement par aspiration et filtrage (climatisation) adéquate plus facile qu'avec les virus seuls très petits.
Reste à les détruire et à éliminer les déchets biologiques.
L'utilisation des plasmides dans les bactéries peuvent servir d'enzymes de striction pour découper l'enveloppe et le noyau du virus,
et en faire des déchets biologiques passifs récupérés par les phages.
- on met de côté l'utilisation du virus comme vecteur de thérapie -
l'approche du Design artistique s'exprime dans la vision 3D virtuelle, où formes et couleurs prennent tout leur sens
pour imager, faire imaginer et simuler mentalement une réalité micro et nanoscopique à la fois structurelle, fonctionnelle et dynamique.
Dans son Design, l'entité biologique macromoléculaire prend toute sa beauté intrigante
dans sa forme et sa plasticité à s'interactivé entre-elles (amines, protéines, enzymes) et le long des structures plus complexes (hélice, ADN, ARN, génome).
L'impression 3D peut en rendre compte dans son esthétique et une forme de Poïétique de la création,
mais également dans l'approche du Design Scientifique
où l'interaction automatique, conversationnelle et interactive avec l'expérimentateur (UX-Design) peut se faire invisio (par la virtualité numérique)
mais également par le concret d'un jeu de construction biomoléculaire comme celui de Zoom-Tools pour les atomes.
Ici les biomolécules constituent les entités premières, entières et déformables selon leurs propriétés
mais aussi s'interconnectant selon leurs liaisons et relations chimiques et leurs formes évolutives
se déplaçant sur les structures, s'agrégeant ou se dispersant, se découpant et se recollant ailleurs pour se dupliquer ou se répliquer, voire se muter.
Ce Bio-Design Tools serait très utile aux expérimentateurs mais également pour la formation des biochimistes et des enfants prodiges, ou pas,
et peut être un passage concret-abstrait-virtuel par le concret à l'analyse et traitement virtuels sur ordinateur et écran interactif.
Les R&D en Génie Biologique et Médical du CREDACI GBM-LAB reprend les travaux des années 1974-89
(Robotique de Laboratoire pour la culture cellulaire et l'imagerie biomédicale 2D et 3D) de façon plus théorique,
mais avec une volonté de simulation dynamique et interactive 3D des Capteurs de Virus Thérapeutiques
pour compenser la saturation et soulager les systèmes immunitaire et respiratoire, en assurant le prétraitement des virus après stockage pour être retraités naturellement.
En effet, nous savons que "the air transports viruses and other pathogens. Since viruses are smaller than other bioaerosols, they have the potential to travel further distances. In one simulation, a virus and a fungal spore were simultaneously released from the top of a building; the spore traveled only 150 meters while the virus traveled almost 200,000 horizontal kilometers." "Aerosols (<5 μm) containing SARS-CoV-1 and SARS-CoV-2 were generated by an atomizer and fed into a Goldberg drum to create an aerosolized environment. The inoculum yielded cycle thresholds between 20 and 22, similar to those observed in human upper and lower respiratory tract samples. SARS-CoV-2 remained viable in aerosols for 3 hours, with a decrease in infection titre similar to SARS-CoV-1. The half-life of both viruses in aerosols was 1.1 to 1.2 hours on average.
The results suggest that the transmission of both viruses by aerosols is plausible, as they can remain viable and infectious in suspended aerosols for hours and on surfaces for up to days."
Ainsi faire des capteurs de virus passe par la culture de bioaérosols de type cellulaire et l'expérimention virale en Robomate de Culture.
Cellules suffisamment petites de grosses bactéries pouvant attirer le virus à l'intérieur pour être traité
à des fins de destruction et/ou d'inaction et de phagisme passif.
Après pulvérisation dans les poumons ou inhalation ou projection dans l'environnement
les virus captés ne peuvent plus nuire immédiatement, directement et indirectement.
Reste à récupérer les capteurs de virus par expectorations et crachats dans des mouchoirs jetables, par pompage,
et pour l'environnement par aspiration et filtrage (climatisation) adéquate plus facile qu'avec les virus seuls très petits.
Reste à les détruire et à éliminer les déchets biologiques.
L'utilisation des plasmides dans les bactéries peuvent servir d'enzymes de striction pour découper l'enveloppe et le noyau du virus,
et en faire des déchets biologiques passifs récupérés par les phages.
Rappels
Biologie, Biochimie cellulaire et macrobiologie génômique
La mobilisation de l’Institut Pasteur pour combattre la pandémie de SARS-CoV-2


Virologie avec travail en Laboratoire manuel et semi-automatique

Fort de son expertise historique en vaccinologie,
l’Institut Pasteur mène actuellement trois projets pour proposer des candidats vaccins contre le COVID-19.


Robotique de Laboratoire pour la Culture Cellulaire
Hotte thermostatée à flux laminaire, et gants de manipulation,
assistée par mini-informatique câblée (Texture Analyser System, TAS de Leitz)
et numérique (PDP 11 de Digital Equipment), avec protocole clinique programmable et interactif sur Apple II.
avec pilotage du Robomate : ensemble numérique programmable
d'un robot avec outil de préhension pour le déplacement des logettes par 6,
entre l'étuve de stockage à température constante et le microscope avec platine X-Y 2D et le Z pour la netteté et la 3D par défocalisation (microtomie-optique)
et le poste de travail avec utilisation de l'outil de changement de milieu de culture réfrigéré et stocké à l'extérieur.
D'après son protocole clinique, l'Apple II envoie également des commandes de traitement d'image
d'analyse de texture câblée ou programmée des images captées par la caméra sur le microscope.
Problématique de la Covid-19 issue du SARS-CoV-2

Virologie avec travail en Laboratoire manuel et semi-automatique

Fort de son expertise historique en vaccinologie,
l’Institut Pasteur mène actuellement trois projets pour proposer des candidats vaccins contre le COVID-19.
- Le premier projet, qui a reçu un financement de la part de CEPI(Coalition for Epidemic Preparedness Innovations)
repose sur l’utilisation du vaccin de la rougeole comme vecteur d’un nouveau candidat vaccin contre le SARS-CoV-2.
En utilisant le vaccin contre la rougeole comme vecteur, des vaccins recombinants ont pu être conçus pour exprimer des antigènes d’autres agents pathogènes
(fragments du virus du sida, de la dengue, du Nil occidental, de la fièvre jaune, de la fièvre de Lassa, ou d’autres maladies émergentes...)
et leur potentiel vaccinal chez l’homme a pu être démontré dans le cas du Chikungunya (essai de phase III en cours).
Cette stratégie très prometteuse est donc appliquée au SARS-CoV-2 avec la possibilité d’aboutir à une application chez l’homme à l’automne 2021.
- Le deuxième projet vise à développer un candidat-vaccin contre le SARS-CoV-2, basé sur des vecteurs vaccinaux lentiviraux.
L'intérêt des vecteurs lentiviraux vaccinaux réside dans leur grand potentiel d’induction de réponses immunitaires adaptatives durables.
Un vecteur à base de lentivirus a été étudié avec succès dans un essai de phase 1 sur un vaccin contre le VIH, qui a établi son innocuité chez l’homme.
- Le troisième projet consiste à évaluer l’immunogénicité (capacité à induire une réaction immunitaire spécifique)
et l’efficacité (capacité de protection) de candidats vaccins à base d’ADN.
La vaccination par ADN est une technique de protection contre les maladies par injection d’ADN codant pour un antigène d’intérêt.
L’ADN injecté entraîne une réponse immunologique protectrice, par exemple par la production d’anticorps contre l’antigène.
repose sur l’utilisation du vaccin de la rougeole comme vecteur d’un nouveau candidat vaccin contre le SARS-CoV-2.
En utilisant le vaccin contre la rougeole comme vecteur, des vaccins recombinants ont pu être conçus pour exprimer des antigènes d’autres agents pathogènes
(fragments du virus du sida, de la dengue, du Nil occidental, de la fièvre jaune, de la fièvre de Lassa, ou d’autres maladies émergentes...)
et leur potentiel vaccinal chez l’homme a pu être démontré dans le cas du Chikungunya (essai de phase III en cours).
Cette stratégie très prometteuse est donc appliquée au SARS-CoV-2 avec la possibilité d’aboutir à une application chez l’homme à l’automne 2021.
- Le deuxième projet vise à développer un candidat-vaccin contre le SARS-CoV-2, basé sur des vecteurs vaccinaux lentiviraux.
L'intérêt des vecteurs lentiviraux vaccinaux réside dans leur grand potentiel d’induction de réponses immunitaires adaptatives durables.
Un vecteur à base de lentivirus a été étudié avec succès dans un essai de phase 1 sur un vaccin contre le VIH, qui a établi son innocuité chez l’homme.
- Le troisième projet consiste à évaluer l’immunogénicité (capacité à induire une réaction immunitaire spécifique)
et l’efficacité (capacité de protection) de candidats vaccins à base d’ADN.
La vaccination par ADN est une technique de protection contre les maladies par injection d’ADN codant pour un antigène d’intérêt.
L’ADN injecté entraîne une réponse immunologique protectrice, par exemple par la production d’anticorps contre l’antigène.
En 1982
Patrick Saint-Jean, Chef de Projet INSERM (Université de Paris XIII
Bobigny), en culture cellulaire robotisée et en histologie
quantitative, lança la Robotique de Laboratoire pour la culture
cellulaire pour répondre à la demande du responsable de Laboratoire
nommé directeur de Cabinet GBM au Ministère de la Recherche, pour
couvrir une partie des besoins en Imagerie numérique Quantitative et
Automatisation de l'analyse d'image.
Il réalisa un prototype ROBOCULT : hôte à flux laminaire mobile (entre la salle de culture et la salle informatique), contenant
- une zone de stockage (étuve) de boîtes de culture cellulaire à 6 logettes (Gliales transformées vivantes),
- une zone de prise de mesure
(imagerie numérique) par caméra appareillée à un microscope Leitz à
platine (X-Y) avec blocage précis de la boîtes de culture, et focus (Z)
à commande numérique,
- une zone de changement de milieu,
robotisée pour l'ouverture du couvercle des boîtes de culture, la
stérilisation de l’aiguille de ponction et l'évacuation par aspiration
du milieu de culture consommé par la culture et rendu vicieux,
l'injection du nouveau milieu de culture, et la fermeture du couvercle.
Le robot effectue également les déplacement de la boîte de logettes
entre les différents postes de travail.
- une zone (hors hotte à flux
laminaire) de stockage réfrigérée d’une part du milieu de culture frais
et enrichi, pompé selon les besoins, et d’autre part du milieu vicieux
récupéré également par pompe à commande numérique.
- le système ROBOCULT est muni de roulettes et poignées pour la déplacement entre la salle de préparation biologique et la salle informatique. Le stockage des produits est au plus bas en contrepoids, et la hôte à flux laminaire, gardant stérile et isothermique l'enceinte de travail,
est munie d’une porte à glissières pour entrée-sortie stérile et de
deux paires de gants interactifs de chaque côté pour manipulation
interne par des utilisateurs externes.
- La capture et l'analyse d'image câblée rapide est effectué par un TAS de Leizt (Texture Analysis Sytem). L'image obtenue est un ensemble de points gris répartis en 2D. L'organisation relationnelle des sous-ensembles de gris différents (16 à 64) crée des textures caractéristiques des images cellulaires en culture (ou pas) présentées sur le microscope.
- Un PDP 11 de Digital Equipment (DEC) pilote le TAS selon ses fonctionnalités programmables, récupère les images et les résultats d'analyse automatique.
- Un micro-ordinateur Apple II, pilote le microscope, le Robot selon ses fonctionnalités, les entrées-sorties de milieux nourriciés ou usagés, et le TAS via le PDP 11 et le PDP 11 lui-même pour effectuer des traitements et des analyses d'image spécifiques essentiellement programmées par fonction, constituant ainsi une partition de fonctions dans le temps, le tout synchronisé selon un protocole clinique d'expérience pour une durée d'une quinzaine de jours maximum. La partition est visualisée sur l'écran et peut être écrite et modifié conversationnellement et par des fonctions d'auto-programmation à partir de macro-test cliniques prenant des décisions sur l'état de la culture ou fonctionnalités spécifiques (détection d'anomalies ou situation particulière comme usure du milieu provoquant la rétractation des cellules étalées et interconnectées se remettant en boule pour se déplacer vers des zones nourricières plus propice, séquentialisant les phases de croissance et décroissance optimum).
- Les résultats des fonctions de capture, de prétraitement, d'analyse, de traitement d'image réelle et d'image multiparamétrique, et de synthèse de résultats (tableaux de chiffres, courbes, images de gris et pseudo-gris pour marquage, images multiparamétriques) sont stockés sur disques durs amovibles grandes capacités.
- Le TAS effectue automatiquement et séquentiellement des traitements et analyses de textures topologiques (selon la Morphologie Mathématique de Serra et Matheron), alors que le PDP 11 utilise des traitements, en plus des traitements et analyses des textures prétopologiques (selon les théories de Patrick Saint-Jean en Trans-combinatoire, Textures et Texturologies prétopologiques), moins rapides mais plus précises, de processus markoviens prétopologiques pour stabiliser les mesures de textures et prédire l'évolution de la culture.
- La capture et l'analyse d'image câblée rapide est effectué par un TAS de Leizt (Texture Analysis Sytem). L'image obtenue est un ensemble de points gris répartis en 2D. L'organisation relationnelle des sous-ensembles de gris différents (16 à 64) crée des textures caractéristiques des images cellulaires en culture (ou pas) présentées sur le microscope.
- Un PDP 11 de Digital Equipment (DEC) pilote le TAS selon ses fonctionnalités programmables, récupère les images et les résultats d'analyse automatique.
- Un micro-ordinateur Apple II, pilote le microscope, le Robot selon ses fonctionnalités, les entrées-sorties de milieux nourriciés ou usagés, et le TAS via le PDP 11 et le PDP 11 lui-même pour effectuer des traitements et des analyses d'image spécifiques essentiellement programmées par fonction, constituant ainsi une partition de fonctions dans le temps, le tout synchronisé selon un protocole clinique d'expérience pour une durée d'une quinzaine de jours maximum. La partition est visualisée sur l'écran et peut être écrite et modifié conversationnellement et par des fonctions d'auto-programmation à partir de macro-test cliniques prenant des décisions sur l'état de la culture ou fonctionnalités spécifiques (détection d'anomalies ou situation particulière comme usure du milieu provoquant la rétractation des cellules étalées et interconnectées se remettant en boule pour se déplacer vers des zones nourricières plus propice, séquentialisant les phases de croissance et décroissance optimum).
- Les résultats des fonctions de capture, de prétraitement, d'analyse, de traitement d'image réelle et d'image multiparamétrique, et de synthèse de résultats (tableaux de chiffres, courbes, images de gris et pseudo-gris pour marquage, images multiparamétriques) sont stockés sur disques durs amovibles grandes capacités.
- Le TAS effectue automatiquement et séquentiellement des traitements et analyses de textures topologiques (selon la Morphologie Mathématique de Serra et Matheron), alors que le PDP 11 utilise des traitements, en plus des traitements et analyses des textures prétopologiques (selon les théories de Patrick Saint-Jean en Trans-combinatoire, Textures et Texturologies prétopologiques), moins rapides mais plus précises, de processus markoviens prétopologiques pour stabiliser les mesures de textures et prédire l'évolution de la culture.


Robotique de Laboratoire pour la Culture Cellulaire
Hotte thermostatée à flux laminaire, et gants de manipulation,
assistée par mini-informatique câblée (Texture Analyser System, TAS de Leitz)
et numérique (PDP 11 de Digital Equipment), avec protocole clinique programmable et interactif sur Apple II.
avec pilotage du Robomate : ensemble numérique programmable
d'un robot avec outil de préhension pour le déplacement des logettes par 6,
entre l'étuve de stockage à température constante et le microscope avec platine X-Y 2D et le Z pour la netteté et la 3D par défocalisation (microtomie-optique)
et le poste de travail avec utilisation de l'outil de changement de milieu de culture réfrigéré et stocké à l'extérieur.
D'après son protocole clinique, l'Apple II envoie également des commandes de traitement d'image
d'analyse de texture câblée ou programmée des images captées par la caméra sur le microscope.
L'imagerie numérique quantitative comprent le Traitement d'Image cellulaire :
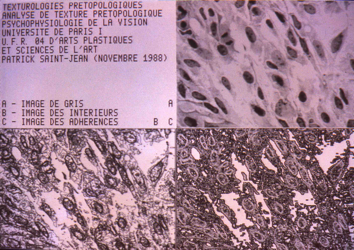
l'Analyse de texture prétopologique statique par répartition des relations (importance-agrégation-dispersion) entre les niveaux de gris,
et dynamiquement par évolution des relations à travers les processus markoviens prétopologiques dans la transition d'états des niveaux de gris :
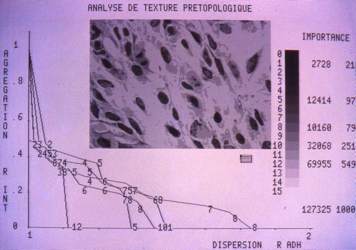
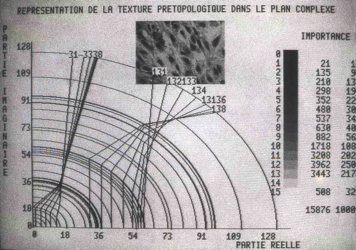
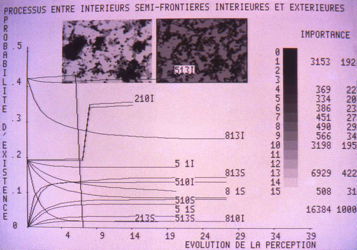
et la classification multiparamétrique multihiérarchique



Image multiparamétrique multihiérarchique (image numérique par ligne et paramètres de texturologie relationnel prétopologique
pour trouver les populations de type de cellules (et artefacts) et d'en faire une typologie et organisation résualiste (en réseau)
Laboratoire du Sylvius Laboratoria de Leiden en Hollande (1987-88).

l'Analyse de texture prétopologique statique par répartition des relations (importance-agrégation-dispersion) entre les niveaux de gris,
et dynamiquement par évolution des relations à travers les processus markoviens prétopologiques dans la transition d'états des niveaux de gris :




et la classification multiparamétrique multihiérarchique



Image multiparamétrique multihiérarchique (image numérique par ligne et paramètres de texturologie relationnel prétopologique
pour trouver les populations de type de cellules (et artefacts) et d'en faire une typologie et organisation résualiste (en réseau)
Laboratoire du Sylvius Laboratoria de Leiden en Hollande (1987-88).
Construction 3D de la mitose in vivo
Après un travail au CEA (CENFAR, Dpt de Protection, 1974-79),
sur les Caryotypes Automatiques et semi-automatiques voir conversationnels
effectuant le repérage des mitoses sur lamelle microscopique
puis leur analyse individuelle pour classifier les 46 chromosomes et artéfacts en classification de Denver,
le RobotMate de Culture Cellulaire (Université Paris Nord, Bobigny, 1981-86)
permet la tomoscopie et microtomographie optique des mitoses cellulaires in vivo.
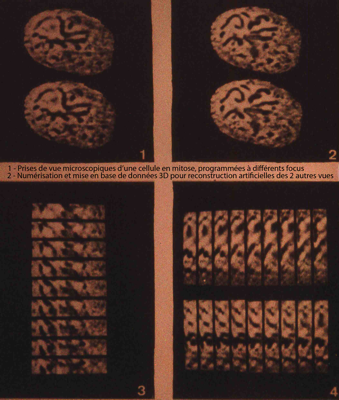
Microtomie optique du champ microscopique (X-Y) par scan en Z pour défocalisation programmée, numérisation et reconstruction numérique selon X-Y, Y-Z et Z-X de la pile d'images.
Depuis, Perkin Elmer réalise différentes hottes à flux laminaire robotisées interconnectables comme Patrick Saint-Jean les avait imaginées,
intégrant également le mise en place dans les logettes de structures plastiques ou siliciques pour analyser les pollutions (toxicité, hydrophobie, etc),
et les formes génératrices de complexes ou de comportements cellulaires (liens gliales-neurones, clones et interclonaux, tissus, aérosols, capteurs de virus, etc.),
rendu possible maintenant par le 3D Printing.


Robotique et Automatisation chemagic™ 360 Nucleic Acid Extractor, Extracteur d'acide nucléique (ARN, ADN) Cell::explorer™Culture cellulaire automatisée basé la technologie brevetée de perles magnétiques de chimagène, solution idéale pour l'isolation de l'acide nucléique (biobanque/génétique humaine, typage HLA, détection de virus et de bactéries)
Après un travail au CEA (CENFAR, Dpt de Protection, 1974-79),
sur les Caryotypes Automatiques et semi-automatiques voir conversationnels
effectuant le repérage des mitoses sur lamelle microscopique
puis leur analyse individuelle pour classifier les 46 chromosomes et artéfacts en classification de Denver,
le RobotMate de Culture Cellulaire (Université Paris Nord, Bobigny, 1981-86)
permet la tomoscopie et microtomographie optique des mitoses cellulaires in vivo.

Microtomie optique du champ microscopique (X-Y) par scan en Z pour défocalisation programmée, numérisation et reconstruction numérique selon X-Y, Y-Z et Z-X de la pile d'images.
Depuis, Perkin Elmer réalise différentes hottes à flux laminaire robotisées interconnectables comme Patrick Saint-Jean les avait imaginées,
intégrant également le mise en place dans les logettes de structures plastiques ou siliciques pour analyser les pollutions (toxicité, hydrophobie, etc),
et les formes génératrices de complexes ou de comportements cellulaires (liens gliales-neurones, clones et interclonaux, tissus, aérosols, capteurs de virus, etc.),
rendu possible maintenant par le 3D Printing.


Robotique et Automatisation chemagic™ 360 Nucleic Acid Extractor, Extracteur d'acide nucléique (ARN, ADN) Cell::explorer™Culture cellulaire automatisée basé la technologie brevetée de perles magnétiques de chimagène, solution idéale pour l'isolation de l'acide nucléique (biobanque/génétique humaine, typage HLA, détection de virus et de bactéries)
Dès 1986, quand le SIDA n’est que très
peu contrer par l’AZT, alors que depuis 1976 (CEA, Paris XIII) il
travaille avec victoria Von Hagen sur les
cellules T4 et les cellules B du Thymus de souris nu, il invente les
« Capteurs de virus » (cellule T4 dénucléarisé ou pas)
contenant des enzymes de striction capables de découper les enveloppes
et noyaux des virus captés et les rendre stériles à la duplication et
propagation.
Ce travail présenté en 1989 au concours de l’INSERM lui vaudra une deuxième place … alors qu’il n’y avait qu’une place pour le "poulain" … et mettra ainsi fin à sa carrière (depuis 1974) de chercheur en GBM.
Cela ne l'empêchera pas de concevoir la suite du concept de "capteur de virus" pour alléger les système immunitaire et respiratoire, et assurer des prétraitements biologiques propice à l'inhibition et l'évacuation dans un recyclage stérile des virus.
Et il en fera des scénarios de science-fiction. Dès 1996, il étendra le concept, lié aux cellules T4, aux grosses bactéries aérosoles capables de capter des virus et de se dupliquer avec eux, le virus pouvant lui-même se dupliquer dans la bactérie.
Autant de virus captés dans la bactérie signifie autant de virus mis hors circuit de l'agression du système immunitaire ou pulmonaire (SIP). Donc un retard possible qui devient intéressant pour soulager le SIP déjà ou risquant d'être en saturation dans son processus de génération d'anticorps et de défense de l'infection bloquant leur réplication et les livrant aux phages pour destruction.
Ce travail présenté en 1989 au concours de l’INSERM lui vaudra une deuxième place … alors qu’il n’y avait qu’une place pour le "poulain" … et mettra ainsi fin à sa carrière (depuis 1974) de chercheur en GBM.
Cela ne l'empêchera pas de concevoir la suite du concept de "capteur de virus" pour alléger les système immunitaire et respiratoire, et assurer des prétraitements biologiques propice à l'inhibition et l'évacuation dans un recyclage stérile des virus.
Et il en fera des scénarios de science-fiction. Dès 1996, il étendra le concept, lié aux cellules T4, aux grosses bactéries aérosoles capables de capter des virus et de se dupliquer avec eux, le virus pouvant lui-même se dupliquer dans la bactérie.
Autant de virus captés dans la bactérie signifie autant de virus mis hors circuit de l'agression du système immunitaire ou pulmonaire (SIP). Donc un retard possible qui devient intéressant pour soulager le SIP déjà ou risquant d'être en saturation dans son processus de génération d'anticorps et de défense de l'infection bloquant leur réplication et les livrant aux phages pour destruction.
La Covid-19 : qu'est-ce qu'un vaccin à base d'ARN messager ?
Les deux premiers vaccins à proclamer leur efficacité, mis
au point respectivement par les laboratoires américains Pfizer et
Moderna, sont basés sur cette technologie.
https://www.francetvinfo.fr/sante/maladie/coronavirus/vaccin/covid-19-qu-est-ce-qu-un-vaccin-a-base-d-arn-messager_4185951.html
Tous deux affirment, par communiqués, avoir trouvé la martingale pour lutter contre le Covid-19, avec des vaccins qui seraient efficaces respectivement à 95%.
Encore faut-il que ces résultats soient publiés dans des revues scientifiques, vérifiés par d'autres chercheurs et, enfin,
agréés par les autorités sanitaires d'éventuels pays acheteurs, à commencer, outre-Atlantique, par la Food and Drug Administration
(FDA, qui délivre l'autorisation de commercialiser les vaccins et médicaments aux Etats-Unis).
Totale nouveauté, les deux vaccins en question sont basés sur l'ARN messager, une séquence codée qui envoie des instructions contre le virus.
De quoi s'agit-il ? Quelles sont les différences avec les vaccins créés contre d'autres virus plus "classiques" ?
Retour sur cette technologie qui n'avait encore jamais été autorisée pour un usage en santé humaine.
La technique traditionnelle des vaccins consiste à injecter un virus inactivé (ou atténué) pour que le corps apprenne à s'en défendre (vaccins à virus atténué ceux contre la fièvre jaune ou la rougeole").
Ainsi le virus infecte alors nos cellules sans nous rendre malade, ce qui le fait repérer par le système immunitaire, qui produit ses défenses.
La technique de l'ARN messager consiste, elle, à envoyer un message à l'organisme sous la forme d'un morceau d'ADN.
Son but est d'inciter l'organisme à fabriquer lui-même une fraction inactive du virus, puis les anticorps pour lutter contre ce virus.
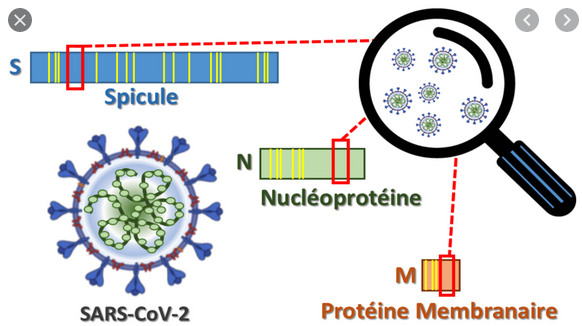
Le vaccin ARN contre le Covid-19 est un fragment d'ARN qui génère la protéine placée sur la surface du virus.
Si le vaccin est efficace, l'organisme va apprendre à reconnaître cette protéine externe, qui s'appelle le spicule du Sars-CoV-2,
et il va générer des réponses immunitaires, sous la forme d'anticorps et de réponse cellulaire.
Les virus inactivés sont obtenus en faisant multiplier le virus, puis à le rendre inactif avec la chaleur, par exemple, ou avec un traitement chimique.
Une entreprise chinoise (Sinovac Life Sciences) a ainsi développé un candidat vaccin contre le Covid-19 sous cette forme inactivée.
L'avantage est le mode de développement qui peut aller très vite dès que l'on connaît la séquence d'un nouveau virus qui émerge.
On peut synthétiser en quelques semaines un fragment d'ADN qui sert de matrice pour le vaccin ARN et une fois qu'on a produit le modèle, on peut facilement le dupliquer à des milliards d'exemplaires.
La technologie de l'ARN messager ne touche pas le noyau de la cellule ; ce qui est très important pour ne pas prendre de risque avec l'ADN.
Le matériel génétique de la personne vaccinée, qui se trouve dans le noyau de la cellule, ne va pas interagir avec l'ARN du vaccin.
La durée d'efficacité des vaccins à ARN n'est pas connu. L'immunité pourrait disparaître plus rapidement qu'avec d'autres vaccins, et il n'y a pas de recul sur cette technologie.
Un risque semble apparaitre : un rétrovirus peut transformer l'ARN en ADN et transformer l'humanité en OGM, organisme génétiquement modifiable qui deviendrait propriété privée de l'industrie mondialz ou des gents de pouvoirs financiers ou politiques.
The power of our platform can be seen in a case study published in 2017 in the Journal of Medicinal Chemistry.
Transform drug discovery and materials research with advanced molecular modeling.
CUTTING THROUGH THE VASTNESS OF CHEMICAL SPACE
Traditional pharma approaches to drug discovery synthesize ~1,000 compounds a year.
The physics-based platform evaluates billions of molecules per week with a high degree of accuracy.
The approach enables discovery of high-quality, novel molecules more rapidly, at lower cost, and believing with a higher likelihood of success compared to traditional methods.
LiveDesign, a linchpin of the platform, enables interactive and collaborative molecule design, aggregation and sharing of data, and end-to-end discovery project coordination between chemists, modelers, and biologists.
Tous deux affirment, par communiqués, avoir trouvé la martingale pour lutter contre le Covid-19, avec des vaccins qui seraient efficaces respectivement à 95%.
Encore faut-il que ces résultats soient publiés dans des revues scientifiques, vérifiés par d'autres chercheurs et, enfin,
agréés par les autorités sanitaires d'éventuels pays acheteurs, à commencer, outre-Atlantique, par la Food and Drug Administration
(FDA, qui délivre l'autorisation de commercialiser les vaccins et médicaments aux Etats-Unis).
Totale nouveauté, les deux vaccins en question sont basés sur l'ARN messager, une séquence codée qui envoie des instructions contre le virus.
De quoi s'agit-il ? Quelles sont les différences avec les vaccins créés contre d'autres virus plus "classiques" ?
Retour sur cette technologie qui n'avait encore jamais été autorisée pour un usage en santé humaine.
La technique traditionnelle des vaccins consiste à injecter un virus inactivé (ou atténué) pour que le corps apprenne à s'en défendre (vaccins à virus atténué ceux contre la fièvre jaune ou la rougeole").
Ainsi le virus infecte alors nos cellules sans nous rendre malade, ce qui le fait repérer par le système immunitaire, qui produit ses défenses.
La technique de l'ARN messager consiste, elle, à envoyer un message à l'organisme sous la forme d'un morceau d'ADN.
Son but est d'inciter l'organisme à fabriquer lui-même une fraction inactive du virus, puis les anticorps pour lutter contre ce virus.
Le vaccin ARN contre le Covid-19 est un fragment d'ARN qui génère la protéine placée sur la surface du virus.
Si le vaccin est efficace, l'organisme va apprendre à reconnaître cette protéine externe, qui s'appelle le spicule du Sars-CoV-2,
et il va générer des réponses immunitaires, sous la forme d'anticorps et de réponse cellulaire.
Les virus inactivés sont obtenus en faisant multiplier le virus, puis à le rendre inactif avec la chaleur, par exemple, ou avec un traitement chimique.
Une entreprise chinoise (Sinovac Life Sciences) a ainsi développé un candidat vaccin contre le Covid-19 sous cette forme inactivée.
L'avantage est le mode de développement qui peut aller très vite dès que l'on connaît la séquence d'un nouveau virus qui émerge.
On peut synthétiser en quelques semaines un fragment d'ADN qui sert de matrice pour le vaccin ARN et une fois qu'on a produit le modèle, on peut facilement le dupliquer à des milliards d'exemplaires.
La technologie de l'ARN messager ne touche pas le noyau de la cellule ; ce qui est très important pour ne pas prendre de risque avec l'ADN.
Le matériel génétique de la personne vaccinée, qui se trouve dans le noyau de la cellule, ne va pas interagir avec l'ARN du vaccin.
La durée d'efficacité des vaccins à ARN n'est pas connu. L'immunité pourrait disparaître plus rapidement qu'avec d'autres vaccins, et il n'y a pas de recul sur cette technologie.
Un risque semble apparaitre : un rétrovirus peut transformer l'ARN en ADN et transformer l'humanité en OGM, organisme génétiquement modifiable qui deviendrait propriété privée de l'industrie mondialz ou des gents de pouvoirs financiers ou politiques.
The power of our platform can be seen in a case study published in 2017 in the Journal of Medicinal Chemistry.
Transform drug discovery and materials research with advanced molecular modeling.
CUTTING THROUGH THE VASTNESS OF CHEMICAL SPACE
Traditional pharma approaches to drug discovery synthesize ~1,000 compounds a year.
The physics-based platform evaluates billions of molecules per week with a high degree of accuracy.
The approach enables discovery of high-quality, novel molecules more rapidly, at lower cost, and believing with a higher likelihood of success compared to traditional methods.
LiveDesign, a linchpin of the platform, enables interactive and collaborative molecule design, aggregation and sharing of data, and end-to-end discovery project coordination between chemists, modelers, and biologists.
Why do proteins fold? Pourquoi une protéine se replie ?
https://foldingathome.org/dig-deeper/
(article de 2016)
Les protéines essaient de se mettre dans leur position la plus "confortable", c'est-à-dire qu'elles sont au meilleur équilibre énergétique avec leur environnement.
Certaines protéines contiennent des zones hydrophobes (répulsion à l’eau), de sorte que
ces sections de la protéine finiront par s'éloigner de l'environnement aqueux en se cachant au milieu de la protéine repliée.
Il y a beaucoup d'autres facteurs qui déterminent la protéine, mais il y a plusieurs analogies différentes qui peuvent être utilisées pour expliquer le processus général.
D'abord, pensez à un énorme ballon de plage qui rebondit sur le flanc d'une montagne abrupte. La balle rebondit plusieurs fois alors qu'elle descend et elle finira par s'arrêter.
Si vous lancez de nouveau le ballon de plage, il y aura des variations aléatoires dans son chemin et il ne finira pas au même endroit.
Si vous répétez ce processus plusieurs fois, vous pouvez déterminer qu'il existe un modèle statistique aux points de repos finaux.
Vous pouvez également voir une diffusion statistique dans le temps nécessaire à l'arrêt de la balle.
La plupart du temps, la balle finira au fond de la vallée de la montagne, mais parfois elle finira dans une autre dépression proche et n'atteindra jamais le point d'arrêt le plus bas possible.
La balle ne fait pas que rebondir, elle roule et glisse selon les pentes pour descendre en utilisant les saddle-points (selle de cheval formée de deux paraboles en inverse perpendiculaire).
Il y a alors optimisation du trajet vers un de ses points d'équilibre, voire le plus bas en optimisant la fonction énergie (ou entropie, variété, diversité) .
Les mouvements atomiques ont un caractère statistique important, tout comme ce mouvement de la balle rebondissante dans la montagne.
Le pliage normal est comme tout le temps où la bille se termine au point le plus bas.
Se replier, c'est comme quand le ballon se retrouve ailleurs.
À certains égards, elle ressemble aussi au stationnement parallèle d’une voiture dans une rue bondée.
Au début, la voiture est exposée, et il faut habituellement plusieurs étapes pour stationner correctement la voiture dans la bonne position.
Parfois, il peut être nécessaire de se retirer légèrement, puis d'essayer à nouveau.
Une protéine fait la même chose. Un observateur peut voir une centaine de voitures similaires stationnées dans cet espace,
et ils en viendraient à comprendre les façons courantes de stationner, et quelles méthodes fonctionnent et celles qui ne fonctionnent pas.
Comme les deux exemples, il est important que de connaître le mouvement d’une protéine pliante, mais également les étapes intermédiaires du chemin.
Les méthodes de simulation construisent des modèles de ces deux propriétés.
L'une des façons qui différencient Folding@home de certains autres projets informatiques distribués (Rosetta@home par exemple) est l'utilisation de la façon de se garer (le trajet, la forme du parcours), et pas seulement l'état final de le voir garé.
Même si c’est un résultat important, il ne permet pas de comprendre comment ou pourquoi une protéine se replie parfois.
En essayant d'étudier tous les chemins possibles que le ballon rebondissant peut emprunter pour descendre la montagne, nous apprenons beaucoup sur la question "Comment en sommes-nous arrivés là ?"
Cela permet d'introduire des changements - comme avec les drogues - dans le processus qui modifie la probabilité de résultats mal pliés.
Le repliement des protéines
(https://fr.wikipedia.org/wiki/Repliement_des_prot%C3%A9ines)
Le repliement des protéines est le processus physique par lequel un polypeptide se replie dans sa structure tridimensionnelle caractéristique dans laquelle il est fonctionnel.
Chaque protéine commence sous forme de polypeptide, transcodée depuis une séquence d'ARNm en une chaîne linéaire d'acides aminés.
Ce polypeptide ne possède pas à ce moment de structure tridimensionnelle développée.
Cependant, chaque acide aminé de la chaîne peut être considéré comme ayant certaines caractéristiques chimiques essentielles.
Cela peut être l'hydrophobie, l'hydrophilie, ou la charge électrique, par exemple.
Elles interagissent entre elles et ces interactions conduisent, dans la cellule, à une structure tridimensionnelle bien définie,la protéine repliée, connue comme l'état natif.
La structure tridimensionnelle résultante est déterminée par la séquence des acides aminés.
Le mécanisme du repliement des protéines n'est pas encore complètement compris, en particulier l'ordre dans lequel les différentes parties se replient.
Le problème est ardu car, par exemple, certaines parties déjà repliées aident au repliement d'autres parties, ce qui rend le problème non linéaire.
La détermination expérimentale de la structure tridimensionnelle d'une protéine est souvent très difficile et coûteuse.
Cependant, la séquence de cette protéine est connue, en particulier depuis le séquençage complet de génomes et la détection automatiques de séquences codantes.
En conséquence, les scientifiques ont essayé d'utiliser plusieurs techniques biophysiques pour replier « manuellement » une protéine, c'est-à-dire de prédire la structure d'une protéine complète à partir de sa séquence.
Si cette méthode a apporté des résultats intéressants avec de courtes protéines, l'état actuel de la science achoppe complètement à prédire la structure tridimensionnelle des protéines intégrales de membranes.
D'autres protéines échappent à cette analyse, par exemple les protéines possédant de nombreux ponts disulfures ou encore des protéines synthétisées sous forme de pré-protéine,
c'est-à-dire sous forme de protéine précurseur clivée par des protéases spécifiques pour acquérir leur maturité.
C'est le cas par exemple de l'insuline.
La structure tridimensionnelle correcte, ou native, est essentielle pour que la protéine puisse assurer sa fonction au sein de la cellule.
L'échec du repliement dans la forme attendue produit des protéines inactives avec des propriétés différentes (par exemple, le prion).
De nombreuses maladies neurodégénératives ou autres sont considérées comme résultant d'une accumulation de protéines « mal repliées ».
Christian Boehmer Anfinsen (prix Nobel de chimie 1972) démontre en 1961 le repliement de la ribonucléase et postule que la conformation finale dépend essentiellement de la succession d'acides aminés qui constitue la protéine.
Toutefois, ce dogme repose sur l'idée que le repliement ne dépend que de contraintes thermodynamiques.
Par la suite, à partir du modèle d'allostérie développé par Monod-Wyman et Changeux, Jeannine Yon et de Michel Goldberg, dans des travaux menés en parallèle, introduisent progressivement en France l'idée d'une contrainte cinétique jouant aussi un rôle dans ces repliements.
La séquence d'acides aminés (ou structure primaire) d'une protéine la prédispose à adopter sa ou ses conformation(s) native(s).
Elle se repliera spontanément pendant ou après sa synthèse.
Alors que ces macromolécules peuvent être considérées comme se « repliant elles-mêmes », le mécanisme dépend également des caractéristiques du cytosol, comme la nature du solvant primaire (eau ou lipide), la concentration de sels, la température, et des protéines chaperonnes.
La plupart des protéines repliées possèdent un cœur hydrophobe dans lequel l'ensemble des chaines latérales hydrophobes stabilisent l'état replié, et des chaînes latérales polaires ou chargées sur leur surface exposée au solvant par lesquelles elles interagissent avec les molécules d'eau environnantes.
Il est généralement admis que la minimisation du nombre de chaînes latérales hydrophobes exposées à l'eau est la principale force motrice du processus de repliement, bien qu'une théorie récemment proposée mette l'accent sur les contributions apportées par la liaison hydrogène.
Le processus de repliement in vivo débute parfois lors de la traduction, c'est-à-dire que la terminaison N de la protéine commence à se replier alors que la portion terminale C de la protéine est toujours en cours de synthèse par le ribosome.
Les protéines spécialisées appelées chaperonnes aident au repliement des autres protéines.
Le système bactérien GroEL, qui aide au repliement des protéines globulaires, est un exemple bien étudié.
Dans les organismes eucaryotes, les protéines chaperonnes sont connues sous le nom de protéines de choc thermique.
Bien que la plupart des protéines globulaires soient capables d'atteindre leur état natif sans assistance, les repliements assistés par les protéines chaperonnes sont parfois nécessaires dans un environnement intracellulaire encombré afin de prévenir l'agrégation ; les protéines chaperonnes sont aussi utilisées pour empêcher les mauvais repliements et les agrégations pouvant se produire en conséquence d'une exposition à la chaleur ou à d'autres changements dans l'environnement cellulaire.
De nombreux scientifiques ont été capables d'étudier plusieurs molécules identiques se repliant ensemble de manière massive.
Au niveau le plus basique, il apparaît que lors de la transition vers l'état natif, une séquence d'acides aminées donnée prend à peu près le même chemin et utilise à peu près les mêmes intermédiaires et états de transition.
Le repliement implique parfois la création de structures secondaires et supersecondaires régulières, particulièrement les hélices alpha et les feuillets bêta, puis de la structure tertiaire.
La formation de la structure quaternaire implique l'« assemblage » ou le « coassemblage » de sous-unités qui se sont déjà repliées.
Les structures d'hélice alpha et de feuillet bêta régulières se replient rapidement car elles sont stabilisées par des liaisons hydrogène, comme l'a établi en premier Linus Pauling.
Le repliement protéique peut impliquer des liaisons covalentes sous la forme de ponts disulfures formés entre deux résidus de cystéine ou la formation de clusters métalliques.
Peu avant d'occuper leur conformation native énergétiquement favorable, les molécules peuvent passer par un état intermédiaire de globule fondu.
Le point essentiel du repliement, cependant, reste que la séquence d'acides aminés de chaque protéine contient l'information spécifiant à la fois la structure native et le chemin pour y accéder.
Ce qui ne veut pas dire que deux séquences d'acides aminés identiques se replient à l'identique.
Les conformations diffèrent selon les facteurs environnementaux par exemple; des protéines similaires se replient différemment selon l'endroit où elles se trouvent.
Le repliement est un processus spontané indépendant de l'apport énergétique des nucléosides triphosphates.
Le passage à l'état replié est principalement guidé par les interactions hydrophobes, la formation de liaisons hydrogène intramoléculaires et les forces de Van der Waals, et est contrarié par l'entropie conformationnelle, qui peut être surmontée par des facteurs extrinsèques comme les protéines chaperonnes.
Dans certaines solutions et sous certaines conditions les protéines ne peuvent se replier dans leurs formes biochimiques fonctionnelles (état natif).
Des températures au-dessus (et parfois en dessous) de l'intervalle dans lequel les cellules vivent causeront le non-repliement des protéines, ou leur dénaturation (c'est une des raisons pour lesquelles le blanc d'œuf est opaque après avoir bouilli).
Des fortes concentrations de solutés, des valeurs de pH extrêmes, des forces mécaniques appliquées, ou encore la présence de dénaturants chimiques peuvent conduire au même résultat.
Une protéine complètement dénaturée ne possède ni structure tertiaire ni structure secondaire, et existe sous forme de pelote aléatoire.
Sous certaines conditions, certaines protéines peuvent se replier à nouveau ; cependant, dans de nombreux cas la dénaturation est irréversible.
Les cellules protègent parfois leurs protéines contre l'influence de la chaleur avec des enzymes connues sous le nom de chaperonnes ou protéines de choc thermique, qui aident les autres protéines à la fois à se replier et à rester pliées.
Certaines protéines ne se replient jamais dans les cellules sans l'aide des protéines chaperonnes, qui sont en mesure d'isoler les protéines les unes des autres, ce qui fait que leur repliement n'est pas interrompu par les interactions avec les autres protéines.
Elles peuvent aussi aider à déplier les protéines mal repliées, en leur donnant une autre chance de se replier correctement.
Cette fonction est cruciale pour prévenir du risque de précipitation en agrégats amorphes insolubles.
Les protéines mal repliées sont responsables des maladies liées au prion comme la maladie de Creutzfeldt-Jakob, l'encéphalopathie spongiforme bovine (ou maladie de la vache folle), les maladies de type amylose comme la maladie d'Alzheimer, et de nombreuses autres formes de protéopathie comme la fibrose cystique.
Ces maladies sont associées à la multimérisation des protéines non repliées dans les agrégats extracellulaires ou les inclusions intracellulaires insolubles.
Il n'est pas établi si les plaques constituent une cause ou un symptôme de la maladie.
La durée globale du procédé de repliement varie drastiquement selon la protéine que l'on considère.
Les repliements les plus lents demandent de plusieurs minutes à plusieurs heures pour se produire, principalement en raison des isomérisations de proline ou de mauvaises formations de liaisons disulfures, et la plupart transitent par des états intermédiaires, un peu comme des points de contrôle, avant que le processus soit achevé.
D'un autre côté, les très petites protéines à simple domaine avec des longueurs allant jusqu'à une centaine d'acides aminés se replient en une seule étape.
Des échelles de temps de quelques millisecondes constituent la norme et les réactions de repliement des protéines les plus rapides connues se produisent en quelques microsecondes.
Le paradoxe de Levinthal indique que si une protéine se replie en échantillonnant toutes les conformations, cela prendrait une durée de temps astronomique pour le faire, même si les conformations étaient échantillonnées à vitesse rapide (de l'échelle de la nanoseconde ou de la picoseconde).
En se basant sur l'observation du fait que les protéines se replient bien plus rapidement que ça, Cyrus Levinthal a proposé qu'une recherche conformationnelle aléatoire ne se produit pas durant le repliement, et que la protéine doit, plutôt, se replier selon un « chemin » préférentiel.
L'étude du repliement des protéines a été très largement amélioré dans ces dernières années par le développement des techniques disposant d'une puissante résolution temporelle.
Ce sont des méthodes expérimentales pour déclencher rapidement le repliement d'une protéine, puis observer la dynamique résultante.
Les techniques rapides en usage large comprennent le mélange ultra-rapide des solutions, des méthodes photochimiques, et la spectroscopie de saut de température par laser.
Parmi les nombreux scientifiques ayant contribué au développement de ces techniques, on trouve Heinrich Roder, Harry Gray, Martin Gruebele, Brian Dyer, William Eaton, Sheena Radford, Chris Dobson, Alan Fersht et Bengt Nölting.
Le phénomène de repliement des protéines fut principalement un effort expérimental jusqu'à l'énoncé de la théorie du paysage d'énergie par Joseph Bryngelson et Peter Wolynes à la fin des années 1980 et au début des années 1990.
Cette approche introduit le principe de moindre frustration qui spécifie que l'évolution a sélectionné les séquences d'acides aminés dans les protéines naturelles de sorte que les interactions entre les chaînes latérales favorisent l'acquisition par la molécule de son état replié.
Les interactions qui ne favorisent pas ce repliement sont identifiées comme telles et « désélectionnées », bien que de la « frustration » résiduelle soit attendue.
Une des conséquences de la sélection de ces séquences par l'évolution est que ces protéines sont généralement censées avoir un processus de repliement au sein d'un « paysage d'énergie orienté » qui pointe largement vers l'état natif.
Cette direction de repliement du paysage d'énergie autorise la protéine à se replier vers l'état natif via n'importe lequel des chemins et des intermédiaires, plutôt que d'être restreint à un seul mécanisme.
Cette théorie est appuyée par des simulations numériques de protéines modèles et a été utilisée pour la prédiction de structures et en conception de protéines.
Les techniques de novo ou ab initio pour la prédiction numérique de structures protéiques sont liées, mais distinctes, aux études sur le repliement des protéines.
La dynamique moléculaire (DM) est un outil important pour l'étude du repliement et de la dynamique des protéines in silico.
En raison du coût numérique, les simulations de repliements par dynamique moléculaire ab initio avec de l'eau explicite sont limitées à des peptides et des très petites protéines.
Les simulations DM de protéines plus grosses restent restreintes aux dynamiques sur la structure expérimentale ou sa structure non-repliée à haute température.
Afin de simuler les processus de repliements longs (au-delà d'une microseconde environ), comme le repliement des protéines de petites tailles (environ 50 résidus) ou plus grosses, des approximations ou des simplifications des modèles de protéines doivent être introduites.
Une approche utilisant des représentations réduites des protéines (des pseudo-atomes représentant des groupes d'atomes sont définis) et des potentiels statistiques ne sont pas seulement utiles dans l'optique d'une prédiction de structure protéique, mais sont aussi capables de reproduire les chemins de repliements.
En raison des plusieurs voies possibles de repliement, il peut exister plusieurs structures possibles.
Un peptide constitué de seulement cinq acides aminés peut se replier en plus de 100 milliards de structures potentielles.
La détermination de la structure repliée d'une protéine est une procédure longue et complexe, impliquant des méthodes comme la diffractométrie de rayons X ou la RMN.
Un des champs de plus grand intérêt est la prédiction des structures natives à partir des seules séquences d'acides aminés en utilisant la bio-informatique et des méthodes de simulations numériques.
Certaines protéines contiennent des zones hydrophobes (répulsion à l’eau), de sorte que
ces sections de la protéine finiront par s'éloigner de l'environnement aqueux en se cachant au milieu de la protéine repliée.
Il y a beaucoup d'autres facteurs qui déterminent la protéine, mais il y a plusieurs analogies différentes qui peuvent être utilisées pour expliquer le processus général.
D'abord, pensez à un énorme ballon de plage qui rebondit sur le flanc d'une montagne abrupte. La balle rebondit plusieurs fois alors qu'elle descend et elle finira par s'arrêter.
Si vous lancez de nouveau le ballon de plage, il y aura des variations aléatoires dans son chemin et il ne finira pas au même endroit.
Si vous répétez ce processus plusieurs fois, vous pouvez déterminer qu'il existe un modèle statistique aux points de repos finaux.
Vous pouvez également voir une diffusion statistique dans le temps nécessaire à l'arrêt de la balle.
La plupart du temps, la balle finira au fond de la vallée de la montagne, mais parfois elle finira dans une autre dépression proche et n'atteindra jamais le point d'arrêt le plus bas possible.
La balle ne fait pas que rebondir, elle roule et glisse selon les pentes pour descendre en utilisant les saddle-points (selle de cheval formée de deux paraboles en inverse perpendiculaire).
Il y a alors optimisation du trajet vers un de ses points d'équilibre, voire le plus bas en optimisant la fonction énergie (ou entropie, variété, diversité) .
Les mouvements atomiques ont un caractère statistique important, tout comme ce mouvement de la balle rebondissante dans la montagne.
Le pliage normal est comme tout le temps où la bille se termine au point le plus bas.
Se replier, c'est comme quand le ballon se retrouve ailleurs.
À certains égards, elle ressemble aussi au stationnement parallèle d’une voiture dans une rue bondée.
Au début, la voiture est exposée, et il faut habituellement plusieurs étapes pour stationner correctement la voiture dans la bonne position.
Parfois, il peut être nécessaire de se retirer légèrement, puis d'essayer à nouveau.
Une protéine fait la même chose. Un observateur peut voir une centaine de voitures similaires stationnées dans cet espace,
et ils en viendraient à comprendre les façons courantes de stationner, et quelles méthodes fonctionnent et celles qui ne fonctionnent pas.
Comme les deux exemples, il est important que de connaître le mouvement d’une protéine pliante, mais également les étapes intermédiaires du chemin.
Les méthodes de simulation construisent des modèles de ces deux propriétés.
L'une des façons qui différencient Folding@home de certains autres projets informatiques distribués (Rosetta@home par exemple) est l'utilisation de la façon de se garer (le trajet, la forme du parcours), et pas seulement l'état final de le voir garé.
Même si c’est un résultat important, il ne permet pas de comprendre comment ou pourquoi une protéine se replie parfois.
En essayant d'étudier tous les chemins possibles que le ballon rebondissant peut emprunter pour descendre la montagne, nous apprenons beaucoup sur la question "Comment en sommes-nous arrivés là ?"
Cela permet d'introduire des changements - comme avec les drogues - dans le processus qui modifie la probabilité de résultats mal pliés.
Le repliement des protéines
(https://fr.wikipedia.org/wiki/Repliement_des_prot%C3%A9ines)
Le repliement des protéines est le processus physique par lequel un polypeptide se replie dans sa structure tridimensionnelle caractéristique dans laquelle il est fonctionnel.
Chaque protéine commence sous forme de polypeptide, transcodée depuis une séquence d'ARNm en une chaîne linéaire d'acides aminés.
Ce polypeptide ne possède pas à ce moment de structure tridimensionnelle développée.
Cependant, chaque acide aminé de la chaîne peut être considéré comme ayant certaines caractéristiques chimiques essentielles.
Cela peut être l'hydrophobie, l'hydrophilie, ou la charge électrique, par exemple.
Elles interagissent entre elles et ces interactions conduisent, dans la cellule, à une structure tridimensionnelle bien définie,la protéine repliée, connue comme l'état natif.
La structure tridimensionnelle résultante est déterminée par la séquence des acides aminés.
Le mécanisme du repliement des protéines n'est pas encore complètement compris, en particulier l'ordre dans lequel les différentes parties se replient.
Le problème est ardu car, par exemple, certaines parties déjà repliées aident au repliement d'autres parties, ce qui rend le problème non linéaire.
La détermination expérimentale de la structure tridimensionnelle d'une protéine est souvent très difficile et coûteuse.
Cependant, la séquence de cette protéine est connue, en particulier depuis le séquençage complet de génomes et la détection automatiques de séquences codantes.
En conséquence, les scientifiques ont essayé d'utiliser plusieurs techniques biophysiques pour replier « manuellement » une protéine, c'est-à-dire de prédire la structure d'une protéine complète à partir de sa séquence.
Si cette méthode a apporté des résultats intéressants avec de courtes protéines, l'état actuel de la science achoppe complètement à prédire la structure tridimensionnelle des protéines intégrales de membranes.
D'autres protéines échappent à cette analyse, par exemple les protéines possédant de nombreux ponts disulfures ou encore des protéines synthétisées sous forme de pré-protéine,
c'est-à-dire sous forme de protéine précurseur clivée par des protéases spécifiques pour acquérir leur maturité.
C'est le cas par exemple de l'insuline.
La structure tridimensionnelle correcte, ou native, est essentielle pour que la protéine puisse assurer sa fonction au sein de la cellule.
L'échec du repliement dans la forme attendue produit des protéines inactives avec des propriétés différentes (par exemple, le prion).
De nombreuses maladies neurodégénératives ou autres sont considérées comme résultant d'une accumulation de protéines « mal repliées ».
Christian Boehmer Anfinsen (prix Nobel de chimie 1972) démontre en 1961 le repliement de la ribonucléase et postule que la conformation finale dépend essentiellement de la succession d'acides aminés qui constitue la protéine.
Toutefois, ce dogme repose sur l'idée que le repliement ne dépend que de contraintes thermodynamiques.
Par la suite, à partir du modèle d'allostérie développé par Monod-Wyman et Changeux, Jeannine Yon et de Michel Goldberg, dans des travaux menés en parallèle, introduisent progressivement en France l'idée d'une contrainte cinétique jouant aussi un rôle dans ces repliements.
La séquence d'acides aminés (ou structure primaire) d'une protéine la prédispose à adopter sa ou ses conformation(s) native(s).
Elle se repliera spontanément pendant ou après sa synthèse.
Alors que ces macromolécules peuvent être considérées comme se « repliant elles-mêmes », le mécanisme dépend également des caractéristiques du cytosol, comme la nature du solvant primaire (eau ou lipide), la concentration de sels, la température, et des protéines chaperonnes.
La plupart des protéines repliées possèdent un cœur hydrophobe dans lequel l'ensemble des chaines latérales hydrophobes stabilisent l'état replié, et des chaînes latérales polaires ou chargées sur leur surface exposée au solvant par lesquelles elles interagissent avec les molécules d'eau environnantes.
Il est généralement admis que la minimisation du nombre de chaînes latérales hydrophobes exposées à l'eau est la principale force motrice du processus de repliement, bien qu'une théorie récemment proposée mette l'accent sur les contributions apportées par la liaison hydrogène.
Le processus de repliement in vivo débute parfois lors de la traduction, c'est-à-dire que la terminaison N de la protéine commence à se replier alors que la portion terminale C de la protéine est toujours en cours de synthèse par le ribosome.
Les protéines spécialisées appelées chaperonnes aident au repliement des autres protéines.
Le système bactérien GroEL, qui aide au repliement des protéines globulaires, est un exemple bien étudié.
Dans les organismes eucaryotes, les protéines chaperonnes sont connues sous le nom de protéines de choc thermique.
Bien que la plupart des protéines globulaires soient capables d'atteindre leur état natif sans assistance, les repliements assistés par les protéines chaperonnes sont parfois nécessaires dans un environnement intracellulaire encombré afin de prévenir l'agrégation ; les protéines chaperonnes sont aussi utilisées pour empêcher les mauvais repliements et les agrégations pouvant se produire en conséquence d'une exposition à la chaleur ou à d'autres changements dans l'environnement cellulaire.
De nombreux scientifiques ont été capables d'étudier plusieurs molécules identiques se repliant ensemble de manière massive.
Au niveau le plus basique, il apparaît que lors de la transition vers l'état natif, une séquence d'acides aminées donnée prend à peu près le même chemin et utilise à peu près les mêmes intermédiaires et états de transition.
Le repliement implique parfois la création de structures secondaires et supersecondaires régulières, particulièrement les hélices alpha et les feuillets bêta, puis de la structure tertiaire.
La formation de la structure quaternaire implique l'« assemblage » ou le « coassemblage » de sous-unités qui se sont déjà repliées.
Les structures d'hélice alpha et de feuillet bêta régulières se replient rapidement car elles sont stabilisées par des liaisons hydrogène, comme l'a établi en premier Linus Pauling.
Le repliement protéique peut impliquer des liaisons covalentes sous la forme de ponts disulfures formés entre deux résidus de cystéine ou la formation de clusters métalliques.
Peu avant d'occuper leur conformation native énergétiquement favorable, les molécules peuvent passer par un état intermédiaire de globule fondu.
Le point essentiel du repliement, cependant, reste que la séquence d'acides aminés de chaque protéine contient l'information spécifiant à la fois la structure native et le chemin pour y accéder.
Ce qui ne veut pas dire que deux séquences d'acides aminés identiques se replient à l'identique.
Les conformations diffèrent selon les facteurs environnementaux par exemple; des protéines similaires se replient différemment selon l'endroit où elles se trouvent.
Le repliement est un processus spontané indépendant de l'apport énergétique des nucléosides triphosphates.
Le passage à l'état replié est principalement guidé par les interactions hydrophobes, la formation de liaisons hydrogène intramoléculaires et les forces de Van der Waals, et est contrarié par l'entropie conformationnelle, qui peut être surmontée par des facteurs extrinsèques comme les protéines chaperonnes.
Dans certaines solutions et sous certaines conditions les protéines ne peuvent se replier dans leurs formes biochimiques fonctionnelles (état natif).
Des températures au-dessus (et parfois en dessous) de l'intervalle dans lequel les cellules vivent causeront le non-repliement des protéines, ou leur dénaturation (c'est une des raisons pour lesquelles le blanc d'œuf est opaque après avoir bouilli).
Des fortes concentrations de solutés, des valeurs de pH extrêmes, des forces mécaniques appliquées, ou encore la présence de dénaturants chimiques peuvent conduire au même résultat.
Une protéine complètement dénaturée ne possède ni structure tertiaire ni structure secondaire, et existe sous forme de pelote aléatoire.
Sous certaines conditions, certaines protéines peuvent se replier à nouveau ; cependant, dans de nombreux cas la dénaturation est irréversible.
Les cellules protègent parfois leurs protéines contre l'influence de la chaleur avec des enzymes connues sous le nom de chaperonnes ou protéines de choc thermique, qui aident les autres protéines à la fois à se replier et à rester pliées.
Certaines protéines ne se replient jamais dans les cellules sans l'aide des protéines chaperonnes, qui sont en mesure d'isoler les protéines les unes des autres, ce qui fait que leur repliement n'est pas interrompu par les interactions avec les autres protéines.
Elles peuvent aussi aider à déplier les protéines mal repliées, en leur donnant une autre chance de se replier correctement.
Cette fonction est cruciale pour prévenir du risque de précipitation en agrégats amorphes insolubles.
Les protéines mal repliées sont responsables des maladies liées au prion comme la maladie de Creutzfeldt-Jakob, l'encéphalopathie spongiforme bovine (ou maladie de la vache folle), les maladies de type amylose comme la maladie d'Alzheimer, et de nombreuses autres formes de protéopathie comme la fibrose cystique.
Ces maladies sont associées à la multimérisation des protéines non repliées dans les agrégats extracellulaires ou les inclusions intracellulaires insolubles.
Il n'est pas établi si les plaques constituent une cause ou un symptôme de la maladie.
La durée globale du procédé de repliement varie drastiquement selon la protéine que l'on considère.
Les repliements les plus lents demandent de plusieurs minutes à plusieurs heures pour se produire, principalement en raison des isomérisations de proline ou de mauvaises formations de liaisons disulfures, et la plupart transitent par des états intermédiaires, un peu comme des points de contrôle, avant que le processus soit achevé.
D'un autre côté, les très petites protéines à simple domaine avec des longueurs allant jusqu'à une centaine d'acides aminés se replient en une seule étape.
Des échelles de temps de quelques millisecondes constituent la norme et les réactions de repliement des protéines les plus rapides connues se produisent en quelques microsecondes.
Le paradoxe de Levinthal indique que si une protéine se replie en échantillonnant toutes les conformations, cela prendrait une durée de temps astronomique pour le faire, même si les conformations étaient échantillonnées à vitesse rapide (de l'échelle de la nanoseconde ou de la picoseconde).
En se basant sur l'observation du fait que les protéines se replient bien plus rapidement que ça, Cyrus Levinthal a proposé qu'une recherche conformationnelle aléatoire ne se produit pas durant le repliement, et que la protéine doit, plutôt, se replier selon un « chemin » préférentiel.
L'étude du repliement des protéines a été très largement amélioré dans ces dernières années par le développement des techniques disposant d'une puissante résolution temporelle.
Ce sont des méthodes expérimentales pour déclencher rapidement le repliement d'une protéine, puis observer la dynamique résultante.
Les techniques rapides en usage large comprennent le mélange ultra-rapide des solutions, des méthodes photochimiques, et la spectroscopie de saut de température par laser.
Parmi les nombreux scientifiques ayant contribué au développement de ces techniques, on trouve Heinrich Roder, Harry Gray, Martin Gruebele, Brian Dyer, William Eaton, Sheena Radford, Chris Dobson, Alan Fersht et Bengt Nölting.
Le phénomène de repliement des protéines fut principalement un effort expérimental jusqu'à l'énoncé de la théorie du paysage d'énergie par Joseph Bryngelson et Peter Wolynes à la fin des années 1980 et au début des années 1990.
Cette approche introduit le principe de moindre frustration qui spécifie que l'évolution a sélectionné les séquences d'acides aminés dans les protéines naturelles de sorte que les interactions entre les chaînes latérales favorisent l'acquisition par la molécule de son état replié.
Les interactions qui ne favorisent pas ce repliement sont identifiées comme telles et « désélectionnées », bien que de la « frustration » résiduelle soit attendue.
Une des conséquences de la sélection de ces séquences par l'évolution est que ces protéines sont généralement censées avoir un processus de repliement au sein d'un « paysage d'énergie orienté » qui pointe largement vers l'état natif.
Cette direction de repliement du paysage d'énergie autorise la protéine à se replier vers l'état natif via n'importe lequel des chemins et des intermédiaires, plutôt que d'être restreint à un seul mécanisme.
Cette théorie est appuyée par des simulations numériques de protéines modèles et a été utilisée pour la prédiction de structures et en conception de protéines.
Les techniques de novo ou ab initio pour la prédiction numérique de structures protéiques sont liées, mais distinctes, aux études sur le repliement des protéines.
La dynamique moléculaire (DM) est un outil important pour l'étude du repliement et de la dynamique des protéines in silico.
En raison du coût numérique, les simulations de repliements par dynamique moléculaire ab initio avec de l'eau explicite sont limitées à des peptides et des très petites protéines.
Les simulations DM de protéines plus grosses restent restreintes aux dynamiques sur la structure expérimentale ou sa structure non-repliée à haute température.
Afin de simuler les processus de repliements longs (au-delà d'une microseconde environ), comme le repliement des protéines de petites tailles (environ 50 résidus) ou plus grosses, des approximations ou des simplifications des modèles de protéines doivent être introduites.
Une approche utilisant des représentations réduites des protéines (des pseudo-atomes représentant des groupes d'atomes sont définis) et des potentiels statistiques ne sont pas seulement utiles dans l'optique d'une prédiction de structure protéique, mais sont aussi capables de reproduire les chemins de repliements.
En raison des plusieurs voies possibles de repliement, il peut exister plusieurs structures possibles.
Un peptide constitué de seulement cinq acides aminés peut se replier en plus de 100 milliards de structures potentielles.
La détermination de la structure repliée d'une protéine est une procédure longue et complexe, impliquant des méthodes comme la diffractométrie de rayons X ou la RMN.
Un des champs de plus grand intérêt est la prédiction des structures natives à partir des seules séquences d'acides aminés en utilisant la bio-informatique et des méthodes de simulations numériques.
How does Folding@home simulate protein folding? Comment Folding@home simule le repliement de protéïne ?
Two key aspects to F@H simulations are adaptive sampling and Markov State Models (MSMs).
The two are used together and are very important as they allow to run efficient simulations.
The two are used together and are very important as they allow to run efficient simulations.
Qu'est-ce que les modèles d'état de Markov?
Le pliage protéique est de nature statistique, de sorte qu'une protéine peut se plier de plusieurs façons.
Le besoin d'une carte pour pouvoir voir le tableau d'ensemble est nécessaire.
Les modèles Markov State (MSM) sont une façon de décrire toutes les conformations (formes) qu'une protéine - ou d'autres biomolécules d'ailleurs - explore
comme un ensemble d'états (c'est-à-dire des structures distinctes) et les taux de transition entre eux.
Ils établissent également les propriétés de mouvement et d’énergie de la protéine en se repliant d’une forme à l’autre.
A partir de toutes ces informations, on observe les facteurs qui ont influencé le pliage, ce qui est particulièrement important si la protéine se déplie.
Une grande partie de la théorie sous-jacente à ces méthodes est assez ancienne, mais leur utilisation a été limitée par les défis inhérents à l'identification d'un ensemble raisonnable d'États.
Les MSM sont particulièrement utiles car ils facilitent la parallélisation entre de nombreux processeurs informatiques en permettant l'agrégation statistique de courtes trajectoires de simulation indépendantes.
Cela remplace la nécessité de trajectoires longues uniques et a donc été largement utilisé par les réseaux informatiques distribués tels que Folding@home et GPUGRID.
De plus, grâce à l'échantillonnage adaptatif, les MSM offrent un moyen d'accroître l'efficacité de la simulation sans introduire de biais ou d'approximations artificiels.
Beaucoup de progrès ont été fait en développant des méthodes de modèle d’état de Markov (MSM, Markov Stat Model, Model de Moor) pour analyser les données produitent avec l’aide de la communauté F@H.
Plusieurs membres du Groupe Pande incluant les Drs. Xuhui Huang et Gregory Bowman, ont développé MSMBuilder, un logiciel open-source utilisé pour construire, analyser et visualiser les MSM.
Depuis sa sortie en 2009, il a été téléchargé plus de 1 600 fois sur les cinq continents et a été utilisé dans au moins 40 publications à ce jour.
Formellement, les MSM sont une application spécifique d'équations maîtres d'espace discret paramétrées à partir de la simulation.
Elles se composent de deux parties :
- un système de partitionement de l'espace d'état X, généralement choisi pour diviser le système en un ensemble d'états métastables ;
- et une équation principale décrivant la cinétique sur X, représentée par une matrice de transition T ou une matrice de vitesse.
L'espace d'état et l'équation de base sont tous deux trouvés à partir de la simulation moléculaire.
La manière précise dont cela se fait varie considérablement.
A quoi ressemble un MSM (Markov Stat Model) ?
Entre les macroétats de la protéine :
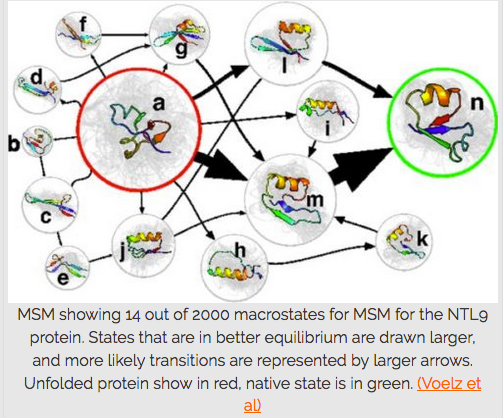

Entre les transitions primaires d'une protéine :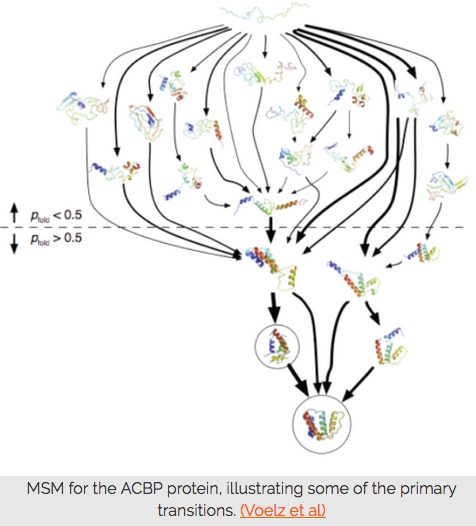
MSM pour la protéine ACBP, illustrant certaines des transitions primaires. (Voelz et al.)
Qu'est-ce que l'échantillonnage adaptatif, et comment est-il lié aux MSM ?
Lorsque les chercheurs utilisent des ordinateurs pour étudier la dynamique conformationnelle des protéines (la façon dont la protéine change de forme au fur et à mesure de son pliage), l’approche conventionnelle pour la dynamique moléculaire non biaisée de tous les atomes est en deux étapes. D'abord, ils exécutent un ensemble de simulations, et ensuite, une fois les simulations terminées, ils analysent les données obtenues.
L'approche adaptative de l'échantillonnage Markov State Model implique de rompre ce paradigme en entrelaçant ces deux étapes. Au lieu de construire le modèle uniquement après la collecte des données, il est construit à la volée au fur et à mesure que les données sont générées. Une boucle de rétroaction peut ensuite être mise en place lorsque l'état actuel du modèle est utilisé pour éclairer l'avancement de nouvelles simulations.
Imaginez, par exemple, que vous exploriez un labyrinthe pour la première fois. Bien que vous n’ayez pas de carte, vous avez un GPS qui vous permet de suivre vos progrès et d’afficher les parties du labyrinthe que vous avez exploré. Une approche est de mettre le GPS dans votre sac et de marcher aveuglément .. renverser les murs .. aussi longtemps que possible. Une fois fatigué, vous sortez le GPS et analysez le chemin que votre trajectoire a suivi ; en regardant votre chemin sur le GPS, vous pouvez voir la structure du labyrinthe et avoir effectivement construit une carte. Malheureusement, vous remarquez que vous avez perdu beaucoup de temps dans différentes parties du labyrinthe. Au lieu de cela, la stratégie la plus intelligente est de regarder le GPS en marchant... pour essayer de construire votre carte du labyrinthe progressivement. En utilisant votre carte, vous pouvez identifier quand vous êtes "coincé" dans une certaine partie du labyrinthe, et éviter de redécouvrir des parties du labyrinthe que vous êtes sûrs d’avoir déjà découvertes.
À bien des égards, ces deux approches de l'exploration d'un labyrinthe sont analogues aux deux approches de la collecte et de l'analyse de simulations moléculaires.
En raison de la nature progressive de la construction du modèle à la volée dans l'approche d'échantillonnage adaptative, il est possible d'augmenter l'efficacité des simulations.
Comment créer un MSM à l'aide d'un échantillonnage adaptatif ?
Pour lancer un projet de simulation, nous devons d’abord choisir quelques conformations initiales (forme d’une protéine).
Les méthodes heuristiques utilisées jusqu’à présent, incluent l’exécution de simulations à haute température, l’utilisation de l’algorithme Monte Carlo de Rosetta et le choix asymétrique parmi les MSM apparentés de protéines similaires. (shooting off related MSMs of similar proteins)
Une fois un ensemble de conformations obtenu, chacune d'entre elles devient le point de départ de certaines simulations appelées ensemble "un Run" ou "Course" ou "Exécution"
A l'intérieur de chaque Course, de nombreuses trajectoires sont lancées, chacune appelée "un Clone".
Ainsi, tous les clones d'une course commencent à partir de la même forme protéique initiale.
Mais ils ont une vitesse initiale différente, c'est-à-dire que les atomes reçoivent une poussée initiale différente dans une direction ou une autre.
Les clones d'une exécution peuvent trouver des conformations supplémentaires, auquel cas les extrémités de la série et plusieurs autres exécutions sont démarrées à partir d'elles.
Ce processus se poursuit avec beaucoup de Runs qui se ramifient à d'autres conformations, fusionnant peut-être ensemble à une forme commune avec d'autres Runs.
Au final, un modèle ayant des dizaines de milliers de conformations différentes, (téraoctets de données !) ayant :
- toutes les formes et les états d'énergie que la protéine peut prendre pendant son repliement vers son "état natif",
- les chances de toutes les transitions se produisant,
- et combien de temps il faut à la protéine pour terminer une transition d'une conformation à une autre.
Plus important encore, l'identification des endroits où les protéines se replient et se coincent, mène ensuite à plus de recherches et de modèles sur la façon d'empêcher cela de se produire.
Plus il y a d'ordinateurs participants, plus vite il est possible de compléter le Modèle d'État de Markov.
Qu’est-ce que les numéros PRCG ?
Les unités de travail sont étiquetées avec quatre numéros distincts dans le format : Project (Run, Clone, Generation), Projet (Exécution, Clone, Génération).
Donc si le projet est la protéine à l'étude :
- un Run est une simulation lancée à partir d'une conformation particulière,
- et Runs contient de nombreux clones qui ont des vitesses initiales différentes.
Bien que Folding@home traite de nombreux projets, exécutions et clones différents en même temps, les clones eux-mêmes sont de nature série.
Ils doivent être simulés du début à la fin, mais il serait peu pratique pour un ordinateur d'en terminer un seul.
Au lieu de cela,
Votre ordinateur reçoit un morceau de clone. La pièce est identifiée en utilisant le numéro Génération (Gen).
Un ordinateur démarrera avec la Génération 0, et quand il finira, à un autre ordinateur sera donné la Génération 1, etc. Le Gen 1 ne peut démarer tant que le Gen 0 n'aura pas fini, et il peut y avoir des centaines de Gens. C'est pourquoi les unités de travail ont des délais et pourquoi la vitesse est si importante.
Pourquoi cette approche est-elle particulièrement utile ?
Cette approche peut être puissante car non seulement elle est très modifiable pour l'informatique distribuée, mais les ressources informatiques disponibles peuvent être utilisées plus efficacement.
Une protéine passe la plupart de son temps de pliage "coincée" dans une position énergétiquement favorable,
avec des transitions - les processus en grande partie intéressants - n'ayant que rarement lieu.
De même, toute simulation simple du pliage de protéines perdra également du temps précieux à produire des données avec peu d'information.
Cependant, en utilisant le concept d'échantillonnage adaptatif, le modèle peut déterminer quand la simulation est bloquée,
puis réinitialiser de nouvelles simulations à partir de zones potentiellement plus fructueuses, en évitant le processus inutile de ré-exploration des zones déjà bien comprises.
Les MSM ont été comparées à des méthodes de simulation plus traditionnelles comme les trajectoires de pliage très longues du superordinateur Anton, à un MSM construit à partir des mêmes données de pliage. Bien que la MSM ait "découpé" la simulation en un tas de trajectoires courtes, il a été capable de reproduire très bien leurs simulations.
De plus, l’approche des MSM a révélé de nouvelles idées sur le processus de pliage (une nouvelle voie de pliage) qui manquait dans l’approche plus traditionnelle d’ANTON.
Quelles sont les applications de ces techniques ?
Les MSM et l'échantillonnage adaptatif ont été utilisés pour étudier le pliage des protéines (1-8),
la dynamique fonctionnelle (8-11), la liaison des ligands (11-14) et les interactions protéine-protéine (15).
Markov State Model (MSM) construction et validation
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3462454/
The MSMBuilder33 software was used to build MSMs for ACBP under folding conditions (0M GuHCl, 330K simulations) and unfolding conditions (0.6–1.0 1M GuHCl, 370K simulations).
We found that a 20,000-microstate decomposition yielded a good balance of state connectivity and adequate transition sampling.
Conformations were clustered using a subset of 258 atoms (backbone N, Cα and C);
20% of the data was used to generate an initial clustering,
and the remaining 80% of the data was assigned to the generators.
The 20,000-microstate model was used for predicting experimental observables, while a 2000-macrostate MSM obtained by kinetic-based lumping 34 was used to analyze the distribution of folding pathway fluxes from unfolded to folded states.
Transition probabilities Tij of transitioning from state i to state j (within a lag time τ) are estimated by counting the number of transitions nij observed between time t and t+τ, and normalizing by rows: Tij = nij/(Σj nij).
To enforce detailed balance, is done the symmetrization of the forward and backward counts as : (nij+nji)/(Σj nij+nji).
Artifacts from symmetrization are mostly limited to transitions with very few counts (and hence low populations that have negligible effects).
Sliding-window counts were used to alleviate finite-sampling errors.
To validate the robustness of these assumptions in estimating transition rates, importance sampling is performed of the posterior distribution of 2000-macrostate transition matrices, using a reversible conjugate prior for Markov chains as described in 35.
Are generated ~5000 Markov chain realizations (samples of transition counts ñij, with no sliding window used; calculations are limited by storage space), from which expectation values (mean and variance) of equilibrium populations pi ∝ (Σj ñij) were calculated.
The expectation equilibrium populations calculated using the reversible prior were very similar to the symmetrization results (Supplementary Fig. S7e,f).
For example, the native macrostate population (pnat) using this procedure was 28.13% +/− 0.069%,
whereas the transition matrix constructed directly from from sliding-window counts yielded pnat = 30.3%, a discrepancy of only ~0.07 kT.
A lag time of τ=20 ns was determined to be suitable by building a series of MSMs at different lag times to find a region where the spectrum of implied timescales 36, 37
τi = −τ/ln(λi) are relatively insensitive to lag time.
To check the accuracy of the MSM, we compared average inter-residue distances over time (17–86, 1–86 and 17–50) seen in the trajectory data, to predictions from the MSM, and found reasonable agreement (see SI section B.1).
While the implied timescales become accelerated after lumping (it is difficult to achieve a perfect separation of timescales), distributions of folding pathway fluxes remain mostly intact for analysis.
A Bayesian inference model described in 38 was used to estimate Arrhenius barriers ΔGij separating microstates and macrostates.
Committor (pfold) values and mean first passage times were computed for each macrostate using methods described in 37, 39.
The pfold values we compute for MSM macrostates are defined as the probability of reaching the native macrostate before the unfolded extended-chain macrostate.
Transition Path Theory (TPT) 40–42 was used to calculate pathways of reactive folding flux, using a modified “greedy backtracking” algorithm (see SI section B.2).
MSM equilibrium population vectors were calculated from the largest eigenvector of the transition matrix, i.e. from peq = peqT.
Macrostate free energies Fi were calculated from MSM equilibrium populations pi as Fi = −kT log pi at room temperature.
The free energy of folding as a function of the kinetic reaction coordinate pfold was calculated as F(pfold) = −kT log Z(pfold) where,
Z(pfold) = Σi χipi where χi is a bin indicator variable for bins with left edges
pfold = 0, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.6, 0.7, 0.8, 0.9, 0.95.
Master Equation formalism
The continuous-time master equation describing the microstate dynamics is dp/dt = pK,
where p is the vector of state populations, and K is a 20,000 × 20,000 matrix of rate coefficients,
related to the discrete-time transition probability matrix by T = exp(τK)
The solution of the master equation is
p(t) = ΣnψLn[ψRn · p(t = 0)] exp(λnt) = Σn pn(t),
where ψLn, ψRn, λn are the left and right eigenvectors and eigenvalues of K, respectively.
The kinetics can thus be described as a superposition of exponential relaxation modes pn(t)
at implied timescales τ*n = −λn−1, each with amplitude an = [ψRn · p(t=0)].
MSM predictions of observables
Predicted values of observables over time were computed as F(t) = p(t) · f, where p(t) is a vector of state populations over time,
and f is a vector of observables values for each microstate.
Uncertainty estimates were propagated assuming statistical independence of each state.
For some observables, time courses were obtained by discrete propagation of the transition probability matrix T, using p(t+τ) = p(t)T.
For others, p(t) was calculated from the 1000 slowest relaxation modes of the master equation solution.
RMSD pseudo-trajectories were calculated using a simple Monte Carlo algorithm to generate a trajectory of (20 ns) microstate jumps,
and selecting at random (uniformly) a simulation snapshot to report observables at each time step (see SI section B.3 for more examples).
Predictions of FRET observables over time were computed with special corrections for FRET probe linkers not present in the simulations (see SI section B.4),
and corrections for native state stability (see below).
Trp-Cys quenching rates and intramolecular diffusion coefficients for T17C-W58 and W58-I86C were predicted using methods described in 25 from simulated distributions of intramolecular Trp-Cys distances P(r) calculated from simulated unfolded ensembles (330 K, 0 M GuHCl and 370 K, 0.6–1.0 M GuHCl, starting from extended
and coil states, snapshots taken after 1 µs), where r is the distance between side-chain centroids (see also SI section A.5).
Intramolecular diffusion coefficients D were computed from trajectory data,
by fitting the mean-squared displacements of Trp-Cys distances over time in blocks of 50 ns (sampled in 1-ns intervals), as described previously.
Correcting predicted FRET (Förster resonance energy transfer) values for native-state stability
A consequence of symmetrization of the transition probability matrix is that the equilibrium populations are proportional to the total number of observed counts : pi ∝ (Σj nij).
Because of this, the MSM predicts an equilibrium distribution of states with ~2:1 unfolded vs. folded populations, even under folding conditions.
To correct predicted observables, the FRET values are compute by subtracting the equilibrium unfolded-state component of the signal (i.e. the simulated unfolded state is “invisible”).
The stationary state peq = (ncoil + next + nnat)/(Ncoil + Next + Nnat) is the (normalized) number of counts observed in the trajectories, where ncoil, next, and nnat are the vectors of observed microstate counts for simulations initiated from coil, extended and native states, respectively,
and N = Ncoil + Next + Nnat is the total number of counts observed in all simulations.
The discrete-time transition matrix is propagated as described above to get populations over time, and calculate FRET using a modified projection operator S′:
S'(p) = (N/Nnat) · [S(p)−S([next + ncoil]/N)]
This projection operator has the property that as t→∞, S'(p(t→∞)) = S(nnat/Nnat).
This correction for the FRET predictions is used in Figure 2d, setting the starting configuration p(t=0) to a single microstate corresponding to the extended state. A caveat of this approach is that negative FRET values may be obtained at very early times, when initial popultaions are from unfolded states. For all case, this effect only occurs for t < 1 µs, faster than the time resolution of the mixer experiments with which comparisons are making.
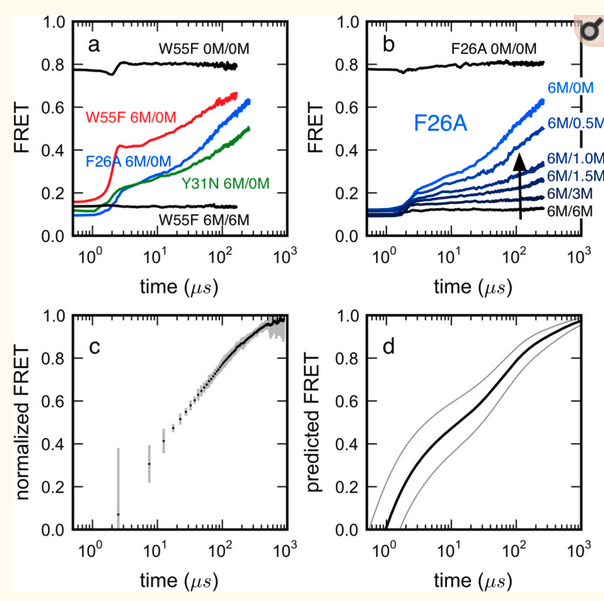 Figure 2
Figure 2
Folding kinetics of hydrophobic core mutants of ACBP 17–88 measured in an ultrafast microfluidic mixer. (a) Mutations F26A and Y31N (shown to disrupt unfolded-state structure in smFRET experiment) decrease the relaxation amplitudes of the fast kinetic phase, but do not significantly affect relaxation rates (see Supplementary Figure S11 and SI section B.4 for fitting details). Burst-phase amplitudes occurring within the mixing time (< 4 µs) are evidence of residual structure already formed at early times. (b) Disruption of residual structure induced by chemical denaturant, exemplified by the F26A variant. (c) Average FRET-trajectories of the W55F variant measured in separate mixing experiments out to ~800 µs. Five independent measurements, normalized to initial and final asymptotic values, were averaged, with the error bars representing the standard deviations of this average. (d) MSM predictions of FRET time courses (see below, Methods) show kinetic time scales in qualitative agreement with experiment. Confidence intervals (thin lines) reflect uncertainty in R0 and probe distances (see SI).
Results
Experimental evidence for a highly structured denatured state
To study the denatured-state structure of ACBP under a wide range of experimental conditions, smFRET studies45,46 were performed. Pairs of Cys residues were engineered into the ACBP sequence (wild type ACBP is Cys-free) that were subsequently labeled with a FRET dye pair (Alexa488/Alexa647). The FRET pairs were positioned such that they report on distance changes within discrete substructures of the four-helix bundle topology (Figure 1a, top).
For example, labeling at position 1–68 reports on distance changes within the first three N-terminal helices, while labeling at positions 17–88 reports on changes in the three C-terminal helices. Likewise, ACBP 1–40 reports predominantly on the integrity and interaction of helix 1 (previously reported to be flexible and engaging in little long-range residual structure4), while ACBP 1–88 probes end-to-end distance changes (SI section A.3 for additional information).
These FRET-pair variants contained an additional, highly destabilizing W55F mutation to populate the denatured subensemble at very low denaturant concentrations. Comparison with wild type ACBP suggests that the W55F mutation does not significantly perturb residual structure in denatured state, at least under conditions where both mutant and wild type populate the denatured state to measurable quantities (0.8–6 M GuHCl) (Supplementary Fig. S1a).
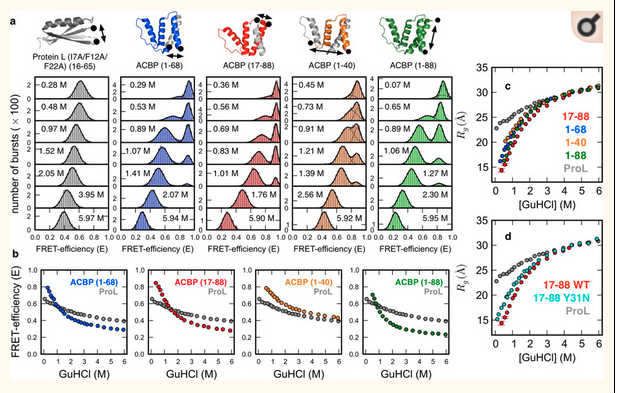
(a) Single molecule FRET histograms measured with site-specifically labeled ProL (grey, reference), and four ACBP variants (blue, red, orange, green) at various denaturant concentrations.
(b) Unfolded-state FRET-efficiencies versus denaturant concentration for each variant, shown with the ProL reference
(c) FRET-based random coil Rg estimates for ACBP revealing non-uniform compaction, and compaction to a greater extent than the ProL random-coil reference. Rg values were normalized to the Rg estimate of ACBP 17–88 by multiplying by the Flory scaling factor (see SI section A.4).
(d) Mutant Y31N produces a significant expansion of the unfolded state, indicating a disruption of long-range structure. (Data for other mutants shown in Supplementary Figure S1.)
FRET-efficiency histograms of the four FRET-pair mutants of ACBP exhibit folded (high-FRET) and unfolded (low-FRET) subpopulations that coexist at intermediate denaturant concentration, as expected for a thermodynamic two state folder with a free energy barrier separating folded and unfolded subpopulations (Figure 1a, bottom).
Mean FRET-efficiencies of the folded and denatured subpopulations were extracted from Gaussian fitting of the histograms. The mean FRET-efficiencies of the denatured subpopulation of each FRET-pair mutant at a particular denaturant concentration are plotted in Figure 1b, together with the mean-FRET efficiency of a highly destabilized and constitutively unfolded triple-Ala variant of ProL (see SI section A.1 for details), that serves here as a pseudo-random coil reference.
Clearly, all four interresidue distances of ACBP probed by smFRET experience significantly larger contractions than the single distance probed in the ProL reference, particularly below 3 M GuHCl, suggesting a compact ensemble of structures under conditions that favor folding.
To compare the mutant effects more quantitatively and to better connect the experimental results with simulation predictions, the FRET-efficiencies are next converted into radii of gyration (Rg), which were then normalized to identical chain length (88 residues) by multiplication with the Flory scaling factor (Figure 1c, SI section A.2 for additional information).
Under strongly denaturing conditions (> 3 M GuHCl), all five proteins show (within error) identical polymer behavior, suggesting that under those conditions, chain contraction is sequence-independent and probably unspecific (see SI section A.3).
Below 3 M GuHCl, however, a significant shortening of each of the four ACBP distances is not only observed beyond that measured in the ProL reference (suggesting acquisition of compact residual structure beyond that seen in the ProL random coil), but also significant differences among the ACBP distances themselves, demonstrating non-uniform compaction. The 1–40 distance exhibits the weakest contraction, which is consistent with previous reports4,47 that helix 1 is more flexible and engages in less residual structure than the remaining three helices.
The largest distance change is experienced by 17–88, with 1–68 exhibiting a behavior in between 1–40 and 17–88. The latter observation is noteworthy, as the interdye distance in 17–88 (72 residues) and 1–68 (68 residues) is almost identical, the only difference being that 17–88 includes the structured C-terminal helix (45 % folded in isolation), while 1–68 includes the weakly structured and more flexible N-terminal helix.
To provide further evidence for residual structure in denatured ACBP, additional mutants were made in the 17–88 FRET-pair context by replacing large, hydrophobic residues that engage in long-range residual structure in folded ACBP (F5A in helix 1, F26A, I27A, Y28A, Y31N in helix 2, and W55L in helix 3; SI section A.3 for additional information). Indeed, for the non-conservative Y31N mutant, a significant perturbation of residual structure (Figure 1d) is observed, a result that is also predicted by reweighting of the simulated unfolding ensembles (Figure 6c, Supplementary Figure S2). Interestingly, even though the F5A mutation perturbs the same long-range interactions as the Y31N in the folded protein, it doesn’t affect denatured-state structure measureably. Perturbation of native-like structure in the denatured ensemble is thus likely not to be the cause of the disruptive effect of the Y31N mutant.
Significant denatured-state expansion in the F26A, I27A and Y28A mutants (Figure S1) is not see, which is perhaps surprising, given that the mutated residues F26, I27, Y28 and Y31 are all positioned in helix 2, and are separated by less than two helix turns in the folded protein. This could simply be because Y31N is more disruptive than the other, more conservative, alanine mutations. Another, more provocative explanation, is that these differential disruptive effects are reporting the presence of specific long-range helix-helix contacts in denatured ACBP. Such an interaction was first postulated by Poulsen and co-workers for helix 2 and helix 4 from spin-sensitized NMR experiments, a hypothesis that is supported by more recent molecular dynamics simulations that reveal similar contacts persisting in acid-denatured ACBP (pH 2.3), i.e. conditions where ACBP is > 99% unfolded. Such long-range interaction might be favored by the amphipathic nature of the two heices and the high helical propensity of helic 4 (60% folded in isolation) that may act as a hydrophobic docking site for helix 2. Indeed a helical wheel plot suggests that residue Y31 would be positioned right in the center of the putative hydrophobic helix interface, while residues F26, I27 and Y28 would adopt more peripheral positions (Supplementary Figure S1b).
It is therefore plausible that a Y31N mutation would exert a more perturbing effect. As the rate-limiting step for folding is the formation of side chain contacts between helices 1, 2 and 4, long-range contacts between helices 2 and 4 in the denatured state might be advantageous for barrier-limited folding1.
A much more extensive mutational analysis, however, is required to fully support this model.
Surprisingly slow formation of unfolded structure
The hypothesize that the ~80 µs kinetic phase seen previously7 might reflect a gradual (microsecond timescale) collapse to a heterogeneous ensemble of unfolded, yet highly compact structures, rather than the formation of a classical folding intermediate.
Strong support for this hypothesis comes from non-equilibrium FRET experiments measured with the F26A, Y31N and W55F mutants of ACBP 17–88 in an ultrafast laminar-flow mixing device.
The FRET-trajectories of the three mutants, measured upon refolding of denatured protein (6 M GuHCl) into refolding buffer (0 M GuHCl), are biphasic, with a submicrosecond burst phase occurring within the mixing time of the mixer (< 4 µs), followed by a fast, kinetically resolvable relaxation process occurring on the ~100 µs timescale (Figure 2a). The W55F trajectory (Figure 2b, red) is best fit by either a single exponential (relaxation time scale = 48 ± 4 µs), or a stretched-exponential (relaxation time scale = 46 ± 3 µs; β = 0.80; see SI section A.4 for further details on curve fitting). Additional measurements for the W55F variant at both high and low flow rates were made in separate mixing experiments to extend the time range of FRET-trajectories to ~800 µs (Figure 2c). The results (after normalization to account for minor differences in detection efficiencies) agree well with the shorter trajectories after 20 µs (see SI section A.4). The full time course of FRET vs. time predicted by the MSM (which does not predict a stable folding intermediate, Figure 5) seems to qualitatively reproduce the ~800 µs FRET-trajectory (Figure 2d). The simulated dynamics predicted by the MSM are slightly faster (~1–10 µs). This agreement with experiment is reasonable considering potential systematic error from forcefield and rate estimation effects (see below).
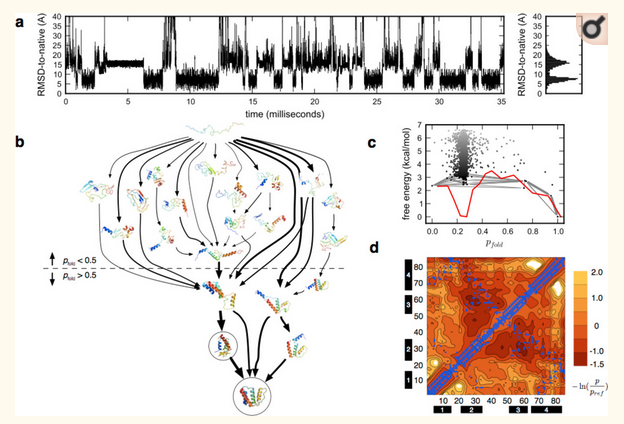
(a) Folding pseudo-trajectories generated from the MSM, projected onto a single degree of freedom such as the RMSD-Cα to the native crystal structure, suggests cooperative folding to the native state via a simple two-state mechanism, near the millisecond timescale. The MSM, however, is a complex network of metastable states, and the full picture of the folding dynamics is predicted to be more complex.
(b) Shown are the 15 highest-flux folding pathways bridging the extended and native states in a 2000-macrostate MSM, as calculated by Transition Path Theory (TPT)41. Line thicknesses are proportional to pathway folding flux (on a log-scale). Circled are the macrostates corresponding to the native and near-native state identified by Teilum et al.2
(c) Free energy vs. pfold (a kinetic reaction coordinate defined as the probability of reaching the native state versus the extended state), plotted for each macrostate (black dots), shows a highly diffuse network of unfolded states, yet a simple basin structure in a 1D projection (red line). Gray edges represent the network of fluxes shown in (b).
(d) Average inter-residue contact propensities calculated from unfolded-state simulations corresponding to ~1M GuHCl (see Methods for details on the conversion of temperature into denaturant concentration), taken after 5 µs, show long-range contacts between helices 2 and 3, and helices 2 and 4. Contours show free energies of contacts (units kT) compared to a reference normalized by loop length. Blue squares denote native contacts.
The slow, barrier-limited folding transition occurring on the ~10 ms time scale, and accounting for the remaining 5–10 % of the expected FRET amplitude change upon folding, cannot be resolved at the high flow rates employed in this study. However, previous laminar-flow mixing studies at substantially slower flow rates and different mixer design revealed an additional slower phase with a rate constant (~ 9 ms) almost identical to the rate constant reported from Trp-fluorescence detection7, thus ruling out a major perturbation of the energy landscape by the bulky fluorophores.
Increasing the denaturant concentration in the refolding buffer results in a nonlinear decrease of the amplitude of the kinetically resolvable relaxation process (Figure 2b). The relaxation rates of the three mutants, obtained from single exponential fits and rate spectra analysis (see below) of the FRET-trajectories, agree within a factor of 2.5 and are only weakly affected by denaturant, as found previously7. Interestingly, mutants Y31N and F26A result in lower dead-time collapse amplitudes than the W55F mutant, indicating that there is already long-range residual structure developing within the first few microseconds of refolding. This hypothesis is supported by earlier experiments and simulations that show that contacts between helices 2 and 3 persist at moderately high denaturant concentrations (3 M GuHCl)4, and our own simulation predictions (see below) that similar interhelical contacts persist at moderately denaturing temperature (370 K, corresponding to 0.6–1.0 M GuHCl) (Supplementary Figure S3). It is therefore plausible that helix 2–helix 3 contacts form early in the folding process while helix 2-helix 4 contacts (which form at lower denaturant concentrations4) form later. Similar fits for for F26A and Y31N yield ~90 µs and ~120 µs, respectively.
Extrapolations of the (normalized) asymptotic FRET efficiencies estimated from non-equilibrium mixing are founded, agreed within experimental error with the FRET-efficiencies of the denatured subpopulation of ACBP inferred from smFRET experiments at equilibrium (Figure 3). Such good agreement between normalized transient and equilibrium FRET efficiencies is difficult to rationalize in the framework of a folding intermediate (see Discussion).
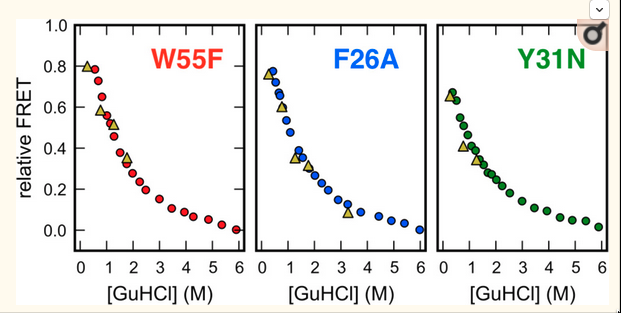
A comparison of relative FRET efficiencies was necessary to account for minor differences in detection efficiencies between the microscopic setups used for the smFRET and ensemble mixing experiments and the presence of donor-only species in the ensemble mixing experiment that were digitally removed in the smFRET experiments. For the smFRET experiments, raw FRET efficiencies of the denatured subpopulation at a particular denaturant concentration were normalized to the difference in FRET efficiency between the folded subpopulation at 0 M GuHCl, and the FRET efficiency of the denatured subpopulation at 6 M GuHCl. For the ensemble mixing experiments, raw asymptotic FRET efficiencies for the microsecond phase at a particular denaturant concentration were normalized to the difference in FRET efficiency of the denatured protein at 6 M (unfolded baseline in Fig. 3a, main text) and the folded protein at 0 M (folded baseline in Fig. 3a, main text). Note that some asymptotic FRET values are not shown: W55F (6 M to 3 M), Y31N (6 M to 1.5 M) and Y31N (6 M to 3 M); these traces were poorly fit by a single-exponential.
Trp-Cys quenching studies suggest slow intramolecular diffusion in the denatured state
To further probe unfolded-state structure and dynamics, Trp-Cys contact quenching studies were performed. These studies measure the time-resolved decay of the excited triplet state of tryptophan, and its quenching by cysteine in the unfolded state, to give insight into intramolecular dynamics in the unfolded state48. Studies were performed for two single-cysteine mutants of the same W55F variant of ACBP which were also used for the smFRET and fast mixing experiments.
The first mutant contains a single Cys at position 17 and probes intramolecular diffusion within the T17C-W58 loop that comprises helices 2 and 3 and the long connecting loop that connects the two helices.
The second mutant contains a Cys at the C-terminus and reports on chain dynamics in the W58-I86C loop, i.e. on dynamics within the two C-terminal helices.
Measurements were performed at equilibrium from 1 M to 6 M GuHCl, as well as in a fast mixer49 which diluted denaturant from 5 M to 0.2 M and 0.8 M GuHCl (0.8 M GuHCl only for T17C-W58) in order to observe intramolecular diffusion before barrier-limited folding.
A previous study has shown good agreement between equilibrium and mixer measurements at the same denaturant concentration49. The observed quenching rates kobs are modeled as resulting from a combination of a reaction-limited rate, kR, and diffusion-limited rate, kD+, which can be extracted by varying viscosity and temperature independently.
An effective diffusion coefficient can be determined from the measured rates and simulated Trp-Cys distance distributions, using methods described previously25 (see SI section A.5). Within the mixer, the observed quenching rate slows down within the mixing time (Figure 4a). The slope of a linear fit of 1/kobs vs. viscosity for W58-I86C gives kD+ = 1.18 ± 0.41 × 105 s−1 at η=1 cP (Figure 4b).
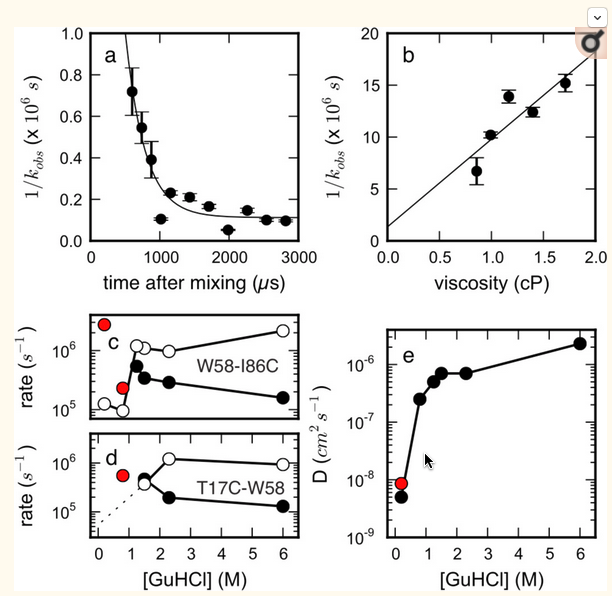
(a) Observed quenching rates vs. time for loop W58-I86C in a fast mixer after diluting from 5 M to 0.2 M GuHCl, shown with an exponential fit to the data.
(b) Linear dependence of W58-I86C quenching times (T=23C) with viscosity at ~1.4 ms, shown with a least-squares linear fit, R2 = 0.729. (T17C-W58 times are not shown as they are too slow to accurately measure.) (c and d) Reaction-limited kR (filled) and diffusion-limited kD+ (open) vs. [GuHCl] for
(c) W58-I86C and
(d) T17C-W58 loops. Red circles denote kR predictions from simulation data, and the dotted line reflects a lower limit of D at 0.2 M (see SI).
(e) Intramolecular diffusion coefficients extracted from the W58-I86C data using SSS theory (see SI section B.4), and the red circle marks D calculated from simulated mean-squared displacements vs. time at 300K (0 M GuHCl).
Qualitatively, the intramolecular dynamics of ACBP exhibits a pattern similar to previously studied proteins (protein L, protein G): Decreasing the denaturant concentration induces a chain compaction, which increases kR and decreases kD+, suggesting less diffusivity (Figures 4c,d). For both loops, kR and kD+ cross at ~1.5 M GuHCl, near the denaturation midpoint, behavior seen previously for protein L, although the midpoint is much lower for ACBP. For the T17C-W58 loop, kD+ becomes too slow to accurately measure (< 4×104 s−1) suggesting this loop is less diffusive than the W58-I86C loop, consistent with the pattern of long-range contacts seen in simulation.
Intramolecular diffusion coefficients at low denaturant concentrations, estimated using experimental rates and a simulated Trp-Cys distribution, were estimated to be ~6 × 10−9 cm2/s, suggesting that the unfolded state in the absence of denaturant is highly collapsed and slowly diffusing, though the level of diffusivity may vary across the chain (Figure 4e).
Significantly, a independent estimate of the diffusion coefficient entirely from simulation gives the same estimate (red point in Figure 4e), showing agreement between simulation and experiment. This result is ~10 times higher than observed for protein L49, despite the fact that it is more compact (see also Figure 1b). The diffusion coefficient decreases dramatically below the denaturation midpoint. Along with the crossing of kR and kD+, and the dramatic increase in FRET from single molecule studies at the denaturant midpoint, this behavior shows the unfolded chain becomes compact and undergoes slow dynamics as the probability of folding becomes significant.
A Markov State Model of ACBP folding predicts a complex network of metastable states
Recently, discrete-state master equation or Markov state models (MSMs) have had success at modeling long-time statistical dynamics11,12,42,43,50.
In these kinetic network models, metastable states are identified such that conformational transitions within each state are much faster than transitions between states, so that the process can be considered to be Markovian51.
The transition rates between states are estimated from Molecular Dynamics (MD) simulations. If the model can self-consistently reconstruct the statistical dynamics of the trajectories it was constructed from, and if it obeys the Markov property, it can be used to simulate the statistical evolution of a non-interacting ensemble of molecules over much longer timescales than the lengths of the individual trajectories from which it is constructed (validation efforts described in Methods).
MSM dynamics can be directly compared with bulk experimental data by computing observables from the predicted state populations over time, as expectation values averaged over each state (see Methods).
MSMs is builded from over 30 milliseconds of atomistic MD simulation trajectories33 (distributions of trajectory lengths are shown in Supplementary Figure S4), for both folding conditions (330 K, 0 M GuHCl) and unfolding conditions (370 K, 0.6–1.0 M GuHCl). The native state is stable at 330 K, with a ~3 Å RMSD-Cα to the crystal structure (PDB code 1hb6) maintained after 1 µs. Trajectories from the 330 K ensemble, initiated from folded and unfolded conformations, were used to construct a 20,000-microstate MSM. The continuous-time master equation solution of the microstate kinetics gives a spectrum of implied timescales (see Methods), with the slowest implied timescale corresponds to the overall folding time. The folding time predicted from the MSM is ~3 ms, comparable to the ~ 9 ms experimental folding time (Supplementary Figure S5).
Although no complete folding events were observed in any one trajectory, the network of microstates is fully connected by the many unfolding and partial re-folding events simulated (Supplementary Fig. S6).
The lowest-free energy microstate contains the native state, and has a cluster center with RMSD-Cα to the crystal structure of ~0.6 Å (Supplementary Fig. S7). The average RMSD-Cα between pairs of conformations in each microstate (i.e. the microstate radius) is 6.89 ± 1.47 Å, slightly larger than previously MSM models of folding (for example, a 100,000-microstate MSM built from simulations of NTL9 (1–39)11 had an average microstate radius of ~4.5Å), due to the larger size of ACBP (86 residues) and the correspondingly larger accessible conformational volume.
For comparison, an MSM is builted from the 370 K data. The average microstate radius in this model was 8.40 ± 1.88 Å. The lowest free-energy microstate still contains the native state, although the relative free energies of the other microstates are lower (Supplementary Fig. S7). For the discussion below, we will restrict our attention to the 330 K MSM constructed for folding conditions.
Macroscopically, the MSM predicts cooperative transitions between the folded and denatured subpopulations on the millisecond timescale, consistent with experiment (Figure 5a). Microscopically, however, the model is considerably more complex. Consistent with recent simulation and experimental studies showing kinetic heterogeneity52, our MSM model predicts a striking heterogeneity of metastable states and folding pathways existing on the mesoscopic scale. MSMs of protein folding for several proteins have previously been reported to have a hub-like network of states around the native state12,38,53. We report a similar hub-like structure for ACBP, consistent with these findings. Mean first passage times (MFPTs) to the native microstate are three orders of magnitude faster than MFPTs to non-native states (Supplementary Figure S8).
A 2000-macrostate MSM obtained from the 20,000-microstate MSM by kinetic-based lumping34 was used to analyze the distribution of folding pathway fluxes from unfolded to folded states. The highest-flux pathways connecting a fully extended state to the native state show contact formation between helices 1 and 4 that are coupled to the folding transition, consistent with phi-value analysis by Kragelund et al1 (Figure 5b). Furthermore, our model predicts a near-native state with a displaced helix 3, corresponding well to a near-native intermediate identified by Teilum et al2.
A surprising feature predicted by the MSM is the absence of a single well-defined folding intermediate postulated in earlier kinetic studies. The free energy of folding as a function of the kinetic reaction coordinate pfold was calculated as F(pfold) = −kT log Z(pfold) where, Z(pfold) was estimated at 300K as the sum of equilibrium macrostate populations for binned values of pfold (see Methods). The free energy diagram shows two low-free energy basins corresponding to the unfolded and folded state, but no other intermediates along the reaction coordinate. Preceding the main folding barrier is a highly diffuse network of compact metastable states with residual unfolded-state structure (Figure 5c). These states contain both native and non-native contacts, consistent with the predictions of past simulations11 and a recent analytical model of hub-like folding networks54.
Unfolded-state compaction in simulated ensembles
Simulated unfolded-state ensembles were generated from trajectories starting from fully extended and random-coil conformations, and used to compute several observables directly comparable with experiment. The extended ensemble shows significant chain compaction by ~100 ns (see SI section B.5), reaching a radius of gyration (Rg) by ~5 µs similar to the coil ensemble, although slightly less compact (Figure 6a), in agreement with previous unfolded-state simulations25. A polymer-theory of the coil-globule transition fits the simulated Rg values well for simulated ensembles at different temperatures (Figure 6a, see Methods, SI section C). While these fits show unrealistically high melting temperatures (as found previously25), they are useful in obtaining transfer free energies per monomer as a function of simulation temperature, which can then be used to find experimental denaturant concentrations where ACBP exhibits a similar extent of chain compaction (see Methods). The comparison of simulated versus experimental Rg obtained by smFRET at the calibrated denaturant concentrations compares favorably (Figure 6b).
To model the sequence-dependent unfolded-state expansions measured by smFRET, a free energy perturbation approach to reweight conformations from simulated unfolded-state ensembles. By using a sufficiently coarse-grained and smooth potential to model sequence perturbations (see Methods; SI section B.6), accurate reweighting was possible using twenty thousand snapshots from simulated unfolded-state ensembles (taken after 5 µs). We calculated expectation values of interresidue distance 17–86 for the simulated wild-type (86-residue) sequence, as well as several mutant sequences characterized by smFRET. Our results generally agree with changes in end-to-end distances observed by smFRET: mutation Y31N is predicted to have the largest disruption of unfolded-state structure, as seen experimentally (Figure 6c). The relatively coarse resolution of our perturbation method, along with effects not accounted for in the model (such as the speculated amphipathic helix packing between helices 2 and 4; see above), are likely the main source of disagreement.
Unfolded-state structure in simulated ensembles
Interresidue contact propensities after 5 µs were calculated for unfolded-state ensembles generated from extended starting structures (see Methods). Similar patterns of unfolded-state structure were found in the low-temperature (330 K, 0 M GuHCl) and high-temperature (370 K, 0.6–1.0 M GuHCl) simulated ensembles. Significant helical secondary structure is predicted for residues in helix 1, 2, and 4 (as calculated by DSSP55, Supplementary Figure S9), in a pattern consistent with chemical shift measurements of the acid-denatured state of ACBP at pH 2.356,57 (Supplementary Figure S10). Consistent with previous NMR chemical shift3 and PRE4 studies, our simulations predict long-range contacts in the unfolded-state ensemble between residues in helix 2 and 3, and helix 2 and 4 (Figure 5d, Supplementary Figure S3). We find fewer contacts involving helix 1, supporting earlier reports that helix 1 is largely detached from the rest of the ACBP structure4, only forming experimentally detectable long-range contacts late in folding reaction3,58. Average RMSD-to-native values for individual helices over time (at 330K starting from the extended state) show helix 1 has a relaxation timescale of ~350 ns, while helices 2, 3 and 4 form compact, non-native structures by ~100 ns, with helix folding/unfolding presumably occurring on timescales slower than ~15 µs (data not shown).
Slightly more helicity (~20%) and more specific long-range contacts (mostly between residues in helix 2 and 3) are seen in the higher temperature simulations (370K, ~0.6–1.0 M GuHCl). This is likely due to the GBSA solvent model used, which does not model temperature-dependent effects, and to the increased conformational sampling at higher temperature. The exact prediction of helix content has little impact on our polymer-theory analysis, as scaling statistics are insensitive to secondary structure content59. We note, however, that overestimates of helicity could bias the folding seen in the MSM toward a ‘diffusion-collision’ mechanism.
Complexity underlies simple kinetics
The network of transition rates in an MSM model specifies a continuous-time chemical master equation whose solution yields a spectrum of implied timescales, each corresponding to a relaxation mode describing population flux on that timescale36,37,43. This spectrum is broad and continuous, reflecting the large number of dynamic transitions between competing metastable states occurring on many timescales (Supplementary Figure S5). This kinetic detail may be difficult to fully resolve experimentally, as structural observables typically report ensemble-averaged quantities, sensitive to specific kinds of structural transitions (e.g. FRET is most sensitive to changes in interatomic distances near the Förster radius.)
Which relaxation modes of ACBP are most sensitively reported by FRET probes? To predict the relaxation timescales observable by the ACBP 17–88 FRET probe, we projected the MSM population dynamics onto a proxy observable, the distance between residues 17 and 86, which can be more easily computed from simulations (since our simulations do not include C-terminal Gly-Cys residues 87 and 88). The predicted (ensemble-average) time course of this proxy distance is a superposition of relaxation modes of different amplitudes (Figure 7a, see Methods). Interestingly, the model shows only two timescale regimes* expected to exhibit a large signal. A prudent experimentalist would fit such observed traces to a bi-exponential curve, postulating a three-state model, even though the underlying dynamics are considerably more complex.
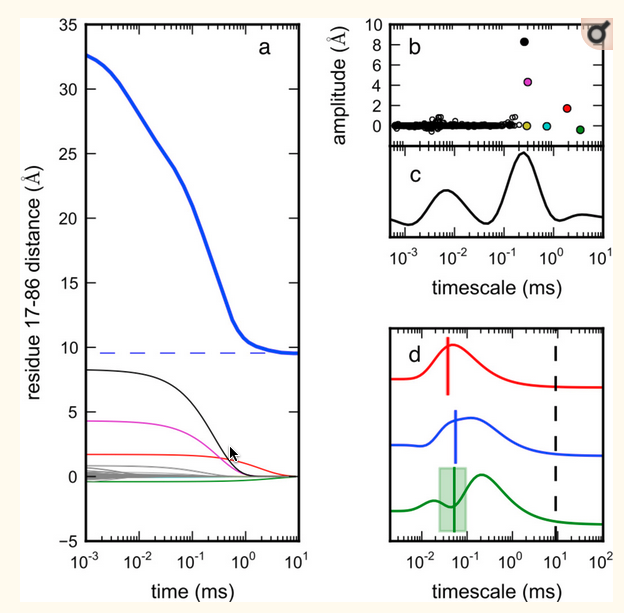
The continuous-time dynamics of the MSM state populations was calculated via the chemical master equation (see Methods). Observable values over time were computed as the sum of projections to the 1000 slowest relaxation modes. Shown in
(a) are the MSM dynamics, starting from initial unfolded populations, projected onto the distance between 17 and 86 (blue, thick), with traces of individual modes shown below this. (Since our simulations do not include the C-terminal Gly-Cys residues, 17–86 is used as a proxy for the FRET distance observable 17–88.)
(b) The amplitudes of each mode, plotted versus each implied timescale, reveal that, despite a broad distribution of kinetic timescales in the model, only two regimes contribute appreciably to the observed signal: ~0.1–3 ms (folding) and ~10 µs (unfolded-state structuring). Note that these timescales are slightly faster than experiment due to forcefield and rate estimation effects.
(c) The calculated rate spectrum for the projection in (a) shows these two regimes clearly.
(d) Rate spectra calculated from experimental FRET mixer traces for W55F, F26A and Y31N (data from Figure 2a) show relaxations corresponding to unfolded-state structuring on the ~100 µs timescale (colored lines and shaded rectangles are timescales calculated from single-exponential fits to the data, and their uncertainties). The ~9 ms folding timescale (black dashed line) is not accessible in the FRET mixer experiments, so peaks corresponding to the global folding rate are absent.
The relaxation modes with significant amplitudes cluster around two important timescale regimes: ~0.1–3.0 ms, corresponding to the overall folding relaxation, and timescales near ~1–10 µs, corresponding to structuring in the unfolded state (Figure 7b). We note that these predicted timescales are faster than experiment by an order of magnitude, with a broad spread in the slowest (folding) relaxation timescales, both of which are likely due to forcefield and transition rate estimation effects. The resolution of the MSM can be improved in the future with additional sampling.
To better compare these predictions to experimental FRET traces, a new method is used to calculate spectra of relaxation timescales from time series data60,61. These so-called rate spectra are obtained by finding a spectrum of rate amplitudes ai such that Σi ai exp(−t/τi) best fits an observed time course for a set of timescales τi. The spectra thus obtained are “dynamical fingerprints”62 of the observed kinetics, and can be thought of as a numerical inverse Laplace transform, in which regularization methods are used to avoid overfitting to noise.
The rate spectra of both simulation data (Figure 7c) and mixer traces (Figure 7d) reveal similar kinetic phases. Rate spectra calculated from experimental FRET mixer traces for W55F, F26A and Y31N (data from Figure 2a) show relaxations corresponding to unfolded-state structuring on the ~100 µs timescale. While experimental limitations (e.g. signal-to-noise) limit the resolution of the rate spectra, a strong qualitative connection between the complex behavior seen in simulation to experiment, as well as quantitative agreement of the location of the peaks in the experimental rate spectra. In most cases, the relaxation timescales obtained from exponential curve fits match the peaks in the rate spectra, although the rate spectra approach is more robust and less sensitive to noise (Supplementary Figure S11, see SI section A.4).
The presence of a very small peak at ~3 ms in the rate spectrum of the simulated time course, near the slowest implied timescale of the MSM. The existence of this separate peak is likely an artifact due to the broad spread of relaxation timescales (~0.1–3 ms), and should be attributed to the folding transition. Inspection of the transition matrix eigenvectors corresponding to each implied timescale show similar structural events for all of these relaxation modes: ensembles of compact unfolded conformations transitioning to the native state (Supplementary Figure S12).
Discussion
Complex, multi-state kinetics is a general phenomenon in biopolymer folding studies, and find it plausible that a great deal of complexity in protein folding is commonly masked in a macroscopic interpretation of ensemble, and even single-molecule experiments62. It is very noteworthy that several new single-molecule studies of protein folding have found conformational fluctuations indicating multiple distinct metastable states63,64. Even the most sophisticated single-molecule experiments, however, cannot resolve the entire microscopic complexity of folding due to the limited number of photons that can be detected on the microsecond timescale. It is therefore likely that ensemble and single molecule fast kinetic observables cannot capture the full complexity of folding, and instead we must turn to computer simulation. Markov State Model approaches is expected to be increasingly useful in this regard, as direct comparisons to experiment can made by projecting predicted microscopic dynamics onto macroscopic observables.
The combined experimental results and MSM of the ACBP folding reaction suggest that residual unfolded-state structure forms on the ~100 µs timescale, in the absence of a well-defined intermediate.
This timescale agrees well with the rates previously reported by Teilum et al. using Trp-Dansyl FRET and a continuous flow mixer7, and the same molecular process is observed in the two studies.
Even in that study, the putative intermediate was described as being mostly unstructured, with only a ~30% increase in buried of surface area compared to the unfolded state, and with the fast ~80 µs kinetic phase insensitive to denaturant concentration.
Intriguingly, our results suggest that the slow formation of unfolded-state structure is not due to barrier-limited formation of a folding intermediate, but rather due to slow unfolded-state structuring, possibly through a continuum of states. Strong agreement is find between the mean-FRET efficiency of the denatured subpopulation at equilibrium and the asymptotic mean-FRET efficiency of the slow, kinetically resolvable phase in the nonequilibrium mixing experiment. In our mixing experiments (from 6 M to 0 M GuHCl), the measured FRET reaches ~90% of the native-state FRET over the course of ~200 µs. This implies that any intermediate I must have native-like FRET (as characterized previously7), and that the unfolded U state must have low FRET and be highly populated at high denaturant concentrations. But if the time-resolved FRET, is indeed due to the relatively slow (~100 µs) interconversion of discrete low-FRET and high-FRET states, significant line-broadening of the denatured subpopulation in the sm-FRET experiments is seen. Such line broadening has been shown by Rieger et al.47 using smFRET with ALEX and a similar confocal transit time to detect an unfolded intermediate of RNase H at ~ 0.7 FRET, differentiated from the native state (0.8 – 1.0 FRET).
A signature of such an intermediate is a very broad unfolded-state FRET histogram that results from averaging and shot noise.
In contrast, the unfolded-state FRET histograms are narrow, comparable with Protein L, which does not populate a folding intermediate.
Although the possibility cannot rule out that U and I substates are obscured by shot noise or fast averaging, and note that we can only make relative comparisons of single-molecule and time-resolved FRET, believing the weight of the evidence argues against the barrier-limited formation of an intermediate.
Instead, the changes in FRET over time observed in the mixer must correspond very closely to the unfolded-state compaction seen in decreasing concentrations of denaturant by smFRET.
Early events in the folding reaction are predicted by the MSM to be structurally heterogeneous, suggesting collapse-like behavior with a gradual acquisition of non-local residual structure.
Non-specific hydrophobic collapse has been characterized as occurring on the ~100 ns timescale65, so slow collapse in ACBP is surprising, although other studies have characterized non-specific collapse forming on timescales less than 150 µs66–68. Consistent with this picture is slow dynamics in protein unfolded states characterized here and elsewhere49, as well as slow dynamics predicted by the MSM.
The Bayesian estimates of average Arrhenius folding barriers separating MSM metastable states38 are small— ~1.64 ± 1.04 kcal/mol for the 20k-microstate model (Supplementary Figure S13)—but the overall hub-like connectivity structure of the network can contribute to slow kinetics.
It is interesting to compare the predictions of unfolded structure with the results of a recent simulation study by Shaw et al. of the acid-denatured unfolded state of ACBP, in which a single 200 µs-trajectory was simulated 47. Tens are obtained of thousands of independent trajectories amounting to tens of milliseconds of aggregate simulation time.
Not surprisingly, even though both simulations predict long-range structure between helices 2 and 4, a great deal more heterogeneity in long-range contacts, reflecting both native and non-native interactions between residues normally participating in the hydrophobic core of ACBP.
The relaxation timescales observed for individual helices is consistent with the faster folding/unfolding timescales of helix 1 observed by Shaw et al.
Conclusion
MSM model of ACBP folding is constructed that reveals a complex network of metastable states with slow dynamics in the unfolded ensemble due to non-random residual structure and heterogeneous folding pathways. Validation of this model using smFRET, intramolecular diffusion and fast microfluidic mixing experiments suggests that the folding reaction for ACBP involves a surprisingly slow acquisition of unfolded-state structure in helix 2, 3 and 4 on the ~100 µs timescale, followed by barrier-limited folding to the native state on the ~10 millisecond timescale.
Moreover, the combined simulation and experimental studies of ACBP show how the microscopic complexity of folding can be reconciled with the simple macroscopic behavior often seen in bulk experiments.
Despite its inherent microscopic complexity, the MSM model of ACBP predicts that experimental observables probing intramolecular distance should exhibit simple bi-exponential kinetics.
In many other molecular systems—vesicle fusion, polymer dynamics, small molecule conformers, etc.—complex dynamics may also underlie simpler experimental observations.
MSM approaches like those described here may provide a general framework for taming these processes and explaining how their simple macroscopic behavior arises.
ABBREVIATIONS
ACBP : acyl-coenzyme A-binding protein
FRET : Förster resonance energy transfer
smFRET : single-molecule FRET
GuHCl : guanidinium hydrochloride
PR : proximity ratio
MSM : Markov State Model
GPU : graphics processing unit
GBSA : generalized Born-surface area
MBAR : multi-state Bennett acceptance ratio
NTL9 : N-terminal domain of ribosomal protein L9
RMSD : root-mean-squared deviation
PRE : paramagnetic relaxation enhancement
https://www.nature.com/articles/s41467-020-19023-1
FRET experiments can provide state-specific structural information of complex dynamic biomolecular assemblies.
However, to overcome the sparsity of FRET experiments, they need to be combined with computer simulations.
A program suite is introduice with (i) an automated design tool for FRET experiments, which determines how many and which FRET pairs should be used to minimize the uncertainty and maximize the accuracy of an integrative structure, (ii) an efficient approach for FRET-assisted coarse-grained structural modeling, and all-atom molecular dynamics simulations-based refinement, and (iii) a quantitative quality estimate for judging the accuracy of FRET-derived structures as opposed to precision.
Tools are benchmarked against simulated and experimental data of proteins with multiple conformational states and demonstrate an accuracy of ~3 Å RMSDCα against X-ray structures for sets of 15 to 23 FRET pairs.
Free and open-source software for the introduced workflow is available at https://github.com/Fluorescence-Tools.
- LabelLib : Library for coarse-grained simulations of probes flexibly coupled to biomolecules. pymol, fluorescence, simulation-toolkit, fret.
- Olga : FRET-screening of conformations and experiment planning. fluorescence, molecules, fret, conformations. C++
- FRETrest : Helper scripts for FRET-restrained MD simulations. Generate AMBER restraint files (DISANG). Python
- FRETlines : Jupyter Notebook
- QuEst - Quenching Estimator for fluorophores coupled to proteins. simulation, fluorescence, fret, quenching, dyes, Jupyter Notebook
Estimateur d'extinction pour les fluorophores couplés aux protéines
- Chisurf : Global analysis platform for fluorescence data. correlation, protein, fluorescence, spectroscopy, multiple-datasets, fluorescence-data,global-analysis, Python
- mdtraj_fps ia a command line tool to calculate FRET observables form MD-trajectories. single-molecule, fluorescence, spectroscopy, Python
Automated and optimally FRET-assisted structural modeling : https://www.nature.com/articles/s41467-020-19023-1
A web server for FRET-assisted structural modeling of proteins
The NMSim Web Interface http://www.nmsim.de Heinrich-Heine-Universität Düsseldorf
NMSim is a normal mode-based geometric simulation approach for exploring biologically relevant conformational transitions in proteins.
The approach has been shown to reproduce experimentally observed conformational variabilities in the case of domain and loop motions and is able to generate meaningful pathways of conformational transitions.
The generated structures are of good stereochemical quality.
Thus, they can serve as input to docking approaches or as starting points for more sophisticated sampling techniques.

The PDB file must not be larger than 5000 atoms.
Structural preparation before simulation:
- Incomplete residues will be fixed.
- Waters and ligands will be removed.
- Hydrogens will be added (are not required for input PDB file).
PDB ID Type of simulation:
- Small scale motions
(loops, docking ensembles, distinct starting structures)
- Large scale motions
(opening and closing of domains)
- Radius of gyration-guided motions
(biased simulation towards lower (or larger) ROG)
Targeted simulation : Target PDB-File
Rigid cluster decomposition parameters (FIRST):
- E-cutoff for H-bonds
- Hydrophobic method
- Hydrophobic cutoff
Normal mode parameters (RCNMA): RCNMA, ENM, Cutoff for C-alpha atoms
Simulation parameters (NMSim):
- No. of trajectories
- No. of NMSim cycles
- Side-chain distortions
- Step size
- No. of sim. cycles
- Output frequency
- NM mode range
- ROG mode
https://pubs.acs.org/doi/10.1021/acs.jpcb.8b10005
Unbiased Atomistic Insight into the Mechanisms and Solvent Role for Globular Protein Dimer Dissociation
L'arrivée du Web et d'Internet a permis de publier inviduellement et en groupe plus rapidement voire même en temps réel, en créant des liens virtuels et en hypertextes à partir ou vers quoi la pensée se pose, réfléchit et évolue selon des références officielles ou "bien pensantes" des gens de pouvoir, pour faire valoir ou se faire valoir, et/ou de la même façon avec des références plus contradictoires menant à la discution plus ou moins profonde et argumentée dans un soucis de s'exprimer et de convraincre soi-même et les autres de ses propre pensées, et de leur fonctionnement dans les systèmes multimédias pour engendrer l'action voire la création.
L'arrivée de Jeu numérique a permis d'utiliser les théories des jeux en général, en stratégies optimisées, pour répondre à des objectifs, des volontés et désirs, et de les intégrer comme projectif à la représentation des concepts sujet-objet-projet, avec l'extansion aux scénario (personnage synthétiques simulant un comportement, une vie propre individuelle), aux mises en scènes (intégrant les acteurs synthétiques dans des environnements actifs et cadre de vie dynamiques, voire mixtes en Réalité Augmentée) et aux mises en jeux avec des gains et/ou des pertes selon des contraintes, des encadrements, des degrés de liberté dans des systèmes de régulation ou de simulation testant les excès en valeur et comportements excessifs, disruptifs ou distorsifs (ou pas, et autres).
Foldit (littéralement « Pliez-la », sous entendant pliez la protéine) est un jeu vidéo expérimental sur le repliement des protéines,
développé en collaboration entre le département d'informatique et de biochimie de l'université de Washington.
La version bêta a été publiée en mai 2008. Les joueurs tentent de résoudre un problème que les ordinateurs ne savent pas résoudre.
Version humaine de Rosetta@home et développée par la même équipe, Foldit utilise les algorithmes de ce dernier, notamment pour le calcul d'énergie des protéines.
De nombreux puzzles proposés aux joueurs de Foldit sont d'ailleurs issus de prévisions calculées par Rosetta.
Un autre exemple de jeu comme celui-ci est le jeu ESP (en) (alias le Google Image Labeler).
Le processus par lequel les êtres vivants créent la structure primaire des protéines, la biosynthèse des protéines, est assez bien compris.
Cependant, déterminer comment la structure primaire d'une protéine se transforme en une structure tridimensionnelle, c'est-à-dire comment la molécule se « plie », est plus difficile.
Le processus général est connu, mais la prédiction des structures protéiques est un calcul compliqué.
Foldit tente d'utiliser les capacités naturelles du cerveau humain pour résoudre ces problèmes (logique, déduction, raisonnement).
Les puzzles actuels sont basés sur des protéines qui sont déjà comprises ;
et c'est en analysant la façon dont les humains abordent ces puzzles que les chercheurs espèrent améliorer les algorithmes employés par les logiciels de pliage des protéines.
Foldit fournit une série de tutoriels dans lesquels l'utilisateur manipule des structures de protéines.
L'application affiche une représentation graphique de la structure de la protéine, et l'utilisateur peut alors la manipuler à l'aide d'un ensemble d'outils.
Lorsque la structure est modifiée, un « score » correspondant au niveau d'énergie de la protéine est calculé en fonction de la façon dont elle est pliée.
Une liste des meilleurs scores pour chaque puzzle est enregistrée.
Les joueurs peuvent automatiser certaines tâches à l'aide de scripts surnommés « recettes ».
Ces scripts, écrits en Lua ont fait l'objet d'une publication de l'équipe de Foldit dans le journal PNAS, certains des algorithmes proposés par ces recettes atteignant des efficacités proches des algorithmes professionnels 1.
Bloqués depuis plus de 10 ans par la complexité de la protéase rétrovirale du virus M-PMV (Mason-Pfizer monkey virus), les chercheurs n'arrivaient pas à trouver sa structure tridimensionnelle.
Cette structure est essentielle pour identifier des sites potentiels que pourraient cibler des protéines-médicament.
Ils ont alors décidé de passer par Foldit et au bout de 3 semaines seulement, la revue Nature Structural & Molecular Biology publie la structure 3D de l'enzyme,
citant au passage les « joueurs » ayant participé à sa découverte comme coauteurs.
Maintenant les biologistes peuvent commencer à chercher des molécules (protéines) capables d'inhiber cette protéase.
Si une telle molécule est trouvée, la reproduction du VIH serait empêchée et l'infection stoppée2.
Genes splicing (épissage des ARN)
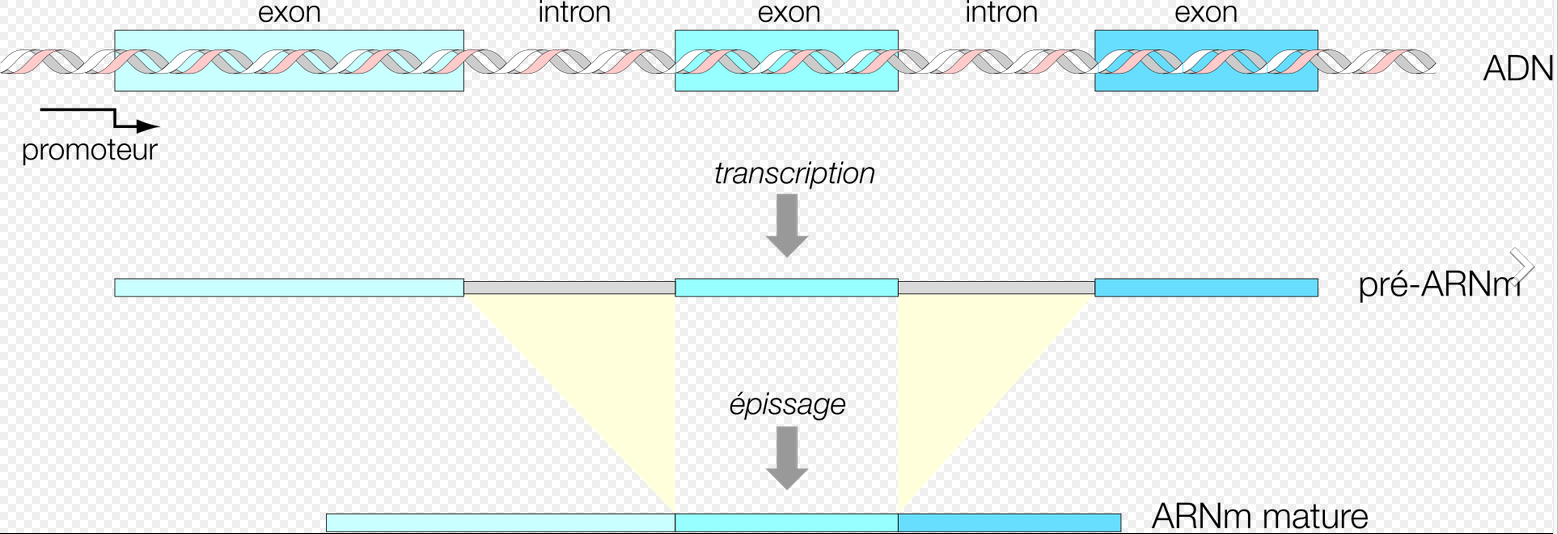
Les mécanismes de contrôle s'assurent que les ARNm ont été correctement épissés avant de permettre leur exportation.
L’épissage est catalysé par un ensemble de complexes ribonucléoprotéiques appelé collectivement spliceosome (épissage se disant splicing en anglais).
Chaque complexe, appelé petite ribonucléoprotéine nucléaire, contient un ARN et plusieurs protéines.
L'épissage des ARNm est également catalysé par les snARN (small nuclear ARN) qui sont de petits ARN non codants liés à des protéines.
Il existe également des introns appelés auto-épissables ou auto-catalytiques, c’est-à-dire capables de s’exciser sans intervention d’un spliceosome, dans les mitochondries, les plastes et certaines bactéries.
Cependant, au moins dans les mitochondries et les chloroplastes, certains de ces introns nécessitent l’intervention de protéines nucléaires.
Le mécanisme catalytique du spliceosome est encore imparfaitement connu, mais par analogie avec le fonctionnement du ribosome, on pense que c'est l’ARN qui est catalytique,
et donc que le spliceosome est un ribozyme, c'est à dire ARN qui possède la propriété de catalyser une réaction chimique spécifique.
Le terme « ribozyme » est un mot-valise formé à partir des mots « acide ribonucléique » et « enzyme ».
L'épissage est beaucoup plus long que la transcription, cette dernière durant quelques minutes contre environ une heure et demie pour l'épissage.
https://endpoints.elysiumhealth.com/three-scientists-who-changed-our-understanding-of-dna-6833c1a057a0
(Elysium Health, Apr 16, 2018).
When scientists from Cambridge University and King’s College London uncovered the structure of DNA six decades ago, they cracked the genetic code and how it’s replicated from one cell to the next, and one generation to the next.
The discovery gave scientists an unprecedented way of studying the root causes of inherited diseases and a potential pathway to cures. It shed light on the aging process, gave way to early sequencing techniques, and eventually set in motion one of the most important scientific projects in history: the Human Genome Project. Today, for the first time ever, we are at a place where scientists can precisely analyze, add to, subtract from, and alter the code of life of every living creature on Earth..
The scientists profiled by the team at Elysium Health, giants in their respective fields, are continuing to tell the story of DNA, fulfilling the promise of genetic sequencing and engineering to solve quandaries in aging and disease, and at the same time, further illuminating what it means to be human.
As part of his dissertation at Harvard in 1984, George Church (Geneticist) developed a direct genome sequencing technique, which contributed to the Human Genome Project (HGP).
Now a professor of genetics at Harvard Medical School and founding core faculty and lead for synthetic biology at the Wyss Institute, Church’s innovations have contributed to nearly all “next generation” DNA sequencing methods and companies.
Church currently directs the Personal Genome Project (PGP), a long-term cohort study that allows scientists to connect human genetic information (human DNA sequence, gene expression, associated microbial sequence data, and more) with human trait information (medical information, biospecimens, and physical traits) and environmental exposures.
“This is still really what my group is focused on, trying to understand what enzymes have improved DNA repair activity in long-lived species, and how that works,” says Gorbunova (Biologist). “Because if we can understand that, maybe we can enhance it.”
While conducting research at Cold Spring Harbor Laboratory in the 1970s, Richard Roberts, Molecular Biologist, discovered RNA splicing, which led to his Nobel Prize in 1993.
When a sequence of DNA is copied it becomes RNA, and RNA contains instructions for making proteins.
During RNA splicing, non-coding regions, called introns, are cut out, and the remaining coding segments, exons, are pasted together to form a mature messenger RNA (mRNA).
Since errors in RNA splicing can result in mutations, scientists use RNA splicing to better understand the underlying mechanisms that cause genetic diseases.
RNA splicing errors account for up to 15 percent of human diseases, ranging from neurological to metabolic disorders.
“This research area is so fundamental that if you want to work on anything that is involved in humans, whether it’s good stuff or bad stuff, whether it’s disease or otherwise, you have to know the structure of the genes, how they’re laid out, how they’re processed, and what goes on. This is just one step along the way.”
These days, Roberts is interested in understanding the biological effects of DNA methylation, a mechanism cells use to control gene expression.
Before CRISPR, Roberts isolated most of the world’s first “molecular scissors.” His groundbreaking work at Jim Watson’s lab, are the similarities between gene splicing and making a movie, and why genetically modified foods aren’t bad.
Gene splicing: The chemical process, involving restriction enzymes, of cutting out part of a DNA in a gene and adding new DNA in its place.
BOINC lets you help cutting-edge science research using your computer.
The BOINC app, running on your computer, downloads scientific computing jobs and runs them invisibly in the background. It's easy and safe.
About 30 science projects use BOINC. They investigate diseases, study climate change, discover pulsars, and do many other types of scientific research.
The BOINC and Science United projects are located at the University of California, Berkeley and are supported by the National Science Foundation.


GPUGRID.net is a distributed computing infrastructure devoted to biomedical research.
RNA World (beta) is a distributed supercomputer that uses Internet-connected computers to advance RNA-related research.
World Community Grid
https://boinc.bakerlab.org/rosetta/
Determine the 3-dimensional shapes of proteins in research that may ultimately lead to finding cures for some major human diseases. By running Rosetta@home you will help us speed up and extend our research in ways we couldn't possibly attempt without your help. You will also be helping our efforts at designing new proteins to fight diseases such as COVID-19, HIV, malaria, cancer, and Alzheimer's
ACEMD Platform is a complete and fast solution package, designed to run and analyze your molecular dynamics (MD) simulations. It includes ACEMD, Parameterize and HTMD packages. ACEMD is the MD engine that runs the simulation, Parameterize is a force field parameterization tool for small molecules and HTMD is a Python package that you can use to create systems, prepare them and, once ACEMD has finished simulating those systems, analyze their trajectories.
Rosetta et le FOLDING sont deux approches différentes, BOINC est une plate-forme ouverte pour la recherche qui permet à de nombreux projets académiques de coexister et puisque le FOLDING n'est pas un projet BOINC, le choix est assez simple au niveau du processeur. GPUGRID est le plus proche de Folding que vous obtiendrez sur la plate-forme BOINC et il fonctionne sur des unités de traitement graphiques au lieu de CPU.
Les protéines sont les éléments constitutifs de notre corps humain et elles sont elles-mêmes constituées de plus petites pièces appelées acides aminés.
Les protéines sont une extraordinaire pièce complexe de machinerie biologique, capable de s'auto-assembler et de transformations et adaptations continues qui sont causées par ce qui se passe autour d'elles.
Elles peuvent changer de forme en fonction de la température, des éléments chimiques présents autour d'eux et d'autres dynamiques, mais peut-être le fait le plus remarquable est que les protéines sont fondamentalement capables de s'auto-assembler à partir de rien en supposant que tout autour d'elles est sans problème.
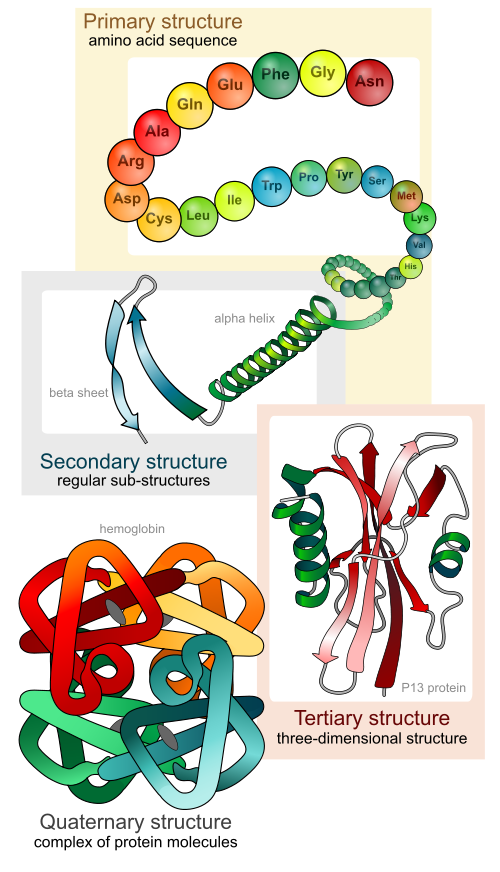
The Institute for Protein Design is located in the Molecular Engineering & Sciences / Nanoengineering & Sciences Building (map) and the J-wing of the Health Sciences Building (map) on the University of Washington Seattle campus.
https://www.ipd.uw.edu/
Designing a new world of proteins to address 21st century challenges in medicine, energy, and technology
https://www.ipd.uw.edu/coronavirus/
The World Health Organization has declared the ongoing COVID-19 outbreak, caused by the virus SARS-CoV-2, a global pandemic. The IPD is focused on seven research projects that we hope will have an immediate impact:
Antiviral and anti-inflammatory proteins : Hyperstable binding proteins are being designed to target the SARS-CoV-2 spike glycoprotein, the human ACE-2 receptor, and receptors implicated in cytokine storms.
(https://www.ipd.uw.edu/wp-content/uploads/2020/09/Cao_COVID_minibindersscience.abd9909.full_.pdf)
Protease inhibitors : A new generation of protease inhibitors made from structured macrocycles with non-canonical residues are being designed to stop SARS-CoV-2 proteases.
Screening existing drugs : Over 8,000 FDA-approved compounds are being screened in silico for binding to structures from the SARS-CoV-2 proteome.
Modeling the viral proteome : Rosetta is being used to model the 3D structures of important proteins from the SARS-CoV-2 coronavirus. (http://new.robetta.org/results.php?id=15652)
Nanoparticle vaccines : Using technology created at the IPD, an array of candidate COVID-19 vaccines has been designed, characterized, and fast-tracked into animal testing.
Serological diagnostics : LOCKR technology is being reconfigured into a sensitive in-solution serological assay to rapidly detect SARS-CoV-2 antibodies in body fluid samples.
Nanoparticles to treat inflammation : New methods for controlling cell signaling are being applied to create new nanoparticle super-agonists for regenerative medicine.
https://www.ipd.uw.edu/research/basic-areas/
Les protéines répondent déjà à une vaste gamme de défis techniques : dans la nature, elles arbitrent l'utilisation de l'énergie solaire pour fabriquer des molécules complexes, répondent à de petites molécules et à la lumière, convertissent des gradients chimiques en liaisons chimiques et transforment l'énergie chimique en travail — pour n'en citer que quelques-unes.
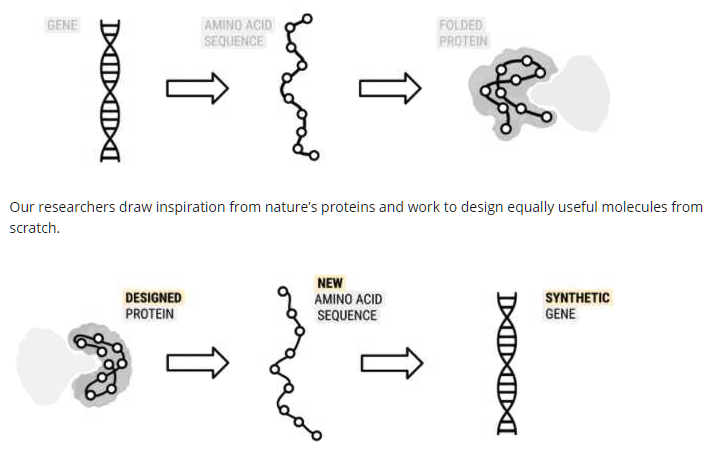 https://www.ipd.uw.edu/audacious/
https://www.ipd.uw.edu/audacious/
Le monde est au bord d'une révolution dans la conception des protéines.
De nouveaux médicaments et matériaux seront programmés sur ordinateur et produits à l'intérieur de cellules vivantes, tirant parti de la pleine échelle et de la durabilité de la biologie.
L'Institute for Protein Design a été un pionnier de longue date dans la conception de protéines computationnelles. Maintenant, grâce à un solide plan directeur et à l'appui du Projet Audacieux, la DPI s'aventurera à accélérer le rythme de la découverte, à diffuser de nouvelles technologies protéiques et à changer fondamentalement la façon dont les médicaments, les vaccins, les carburants et les nouveaux matériaux sont fabriqués.
Les cinq grands défis de l'IPD sont :
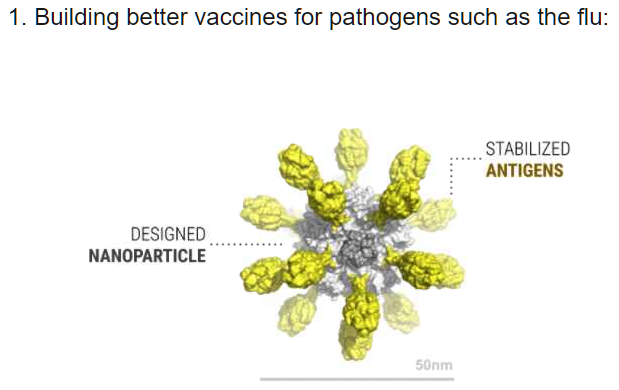
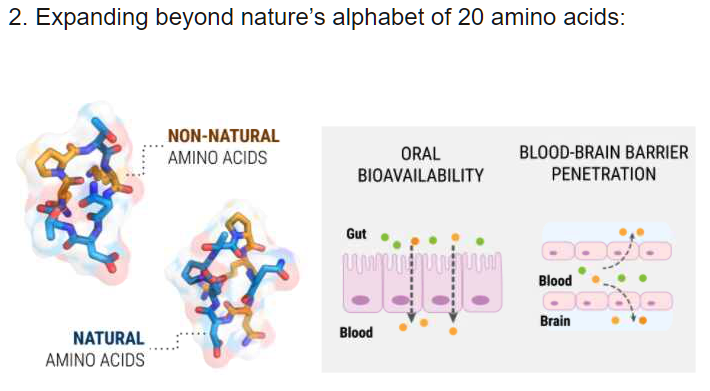
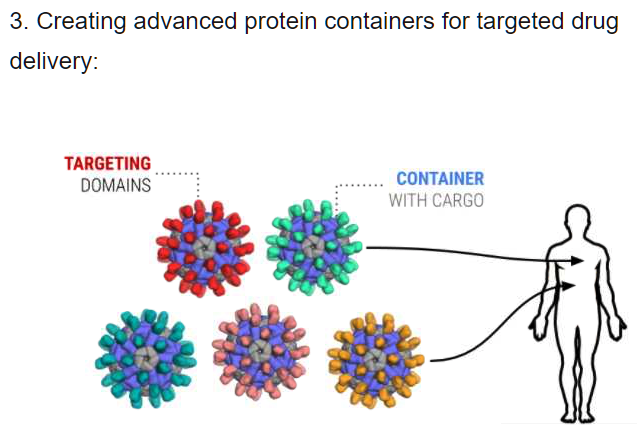
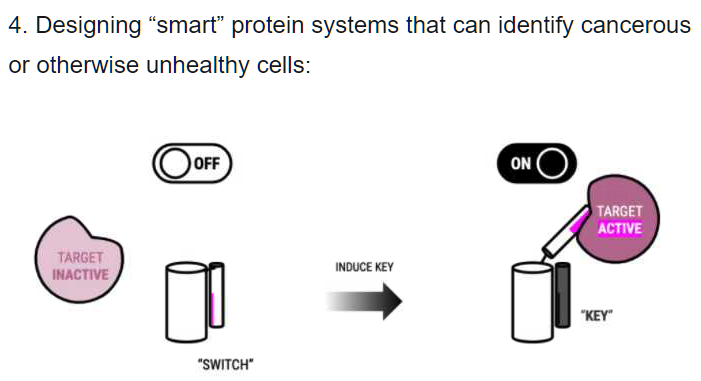

Partant de la problématique :
Les protéines sont des machines moléculaires qui font que tous les êtres vivants vivent leur vie. Elles arrêtent les infections mortelles, guérissent les cellules, captent l'énergie du soleil et bien plus encore.
Les protéines sont construites en liant des blocs chimiques appelés acides aminés, selon les instructions du génome d’un organisme.
Ces cordes "se replient" ensuite, en se basant sur les forces chimiques entre les acides aminés, formant les structures tridimensionnelles complexes nécessaires pour effectuer des tâches spécifiques.
Bien que la nature ait construit des protéines depuis plus de trois milliards d'années, le nombre de protéines possibles est astronomique : il y a plus de façons d'assembler 100 acides aminés qu'il n'y a d'atomes dans l'univers.
Les scientifiques essaient de prédire les formes que les molécules de protéines devraient prendre en fonction de leurs acides aminés — avec un succès limité.
C'est ce qu'on appelle le "problème du pliage des protéines, ou FOLDING
En raison de sa nature insaisissable, comprendre comment exploiter le pouvoir des protéines pour résoudre des problèmes est un problème en soi.
Au cours des 20 dernières années, l’équipe de recherche de David Baker a étudié les règles du pliage des protéines et les a codées dans Rosetta, une simulation informatique
qui a permis de percer dans la compréhension de la façon dont les protéines forment leur structure.
La convergence technologique de Rosetta, à l'essor de l'informatique bon marché et à la révolution génomique dans la lecture et l'écriture de l'ADN,
les chercheurs de l'Institute for Protein Design (IPD) de l'Université de Washington School of Medicine veulent concevoir de nouvelles protéines à partir de zéro avec des fonctions jamais vues dans la nature. Et grace à l'investissement du projet Audacious, l'IPD tente d'accroitre sa capacité de concevoir de nouvelles protéines
et de s'aventurer à modifier fondamentalement la façon dont les médicaments, les vaccins, les carburants et les nouveaux matériaux sont fabriqués.
Encore faut-il bien connaître l'aventure du Covid-19, ses origines et son histoire d'une part pour mieux en comprendre ses processus de vie et de survie qui le motivent à s'installer et se développer comme d'autres de ses semblables dans l'espèce humaine et les autres espèces intermédiaires, et d'autre part d'en trouver les stratégies contradictoires qui le condamnent à aller ailleurs ou pas et sans nuire à l'humanité. D'où le besoin de capteurs de virus avant d'entrée dans le corps humain (systèmes respiratoire et digestif) pour modifier son comportement et les expulser, et dans le corps humain pour les détruire en quantité suffisante pour laisser le système hymunitaire apprendre de leurs structures et fonctions afin d'en générer des anticorps dès plus efficaces.
A l'aide des Texturologies Quantiques Prétopologiques, le High Parallel Computing (HPC) utilisant les Bits-Computers
devient un High Parallel Quantum Computing (HPQC) avec les QBits-Computers
puis un Huge Parallel Texturology Quantum Computing (HUPTQC) avec les TQBits-Computers
et un Huge Parallel Optical Texturology Quantum Computing (HUPOTQC) avec les OTQBits-Computers (Optical Texturology QBits)
Avec myQLM d'ATOS,
nous préparons les NoteBooks myQLM de programmation quantique texturologique
The Atos Quantum Learning Machine (QLM & QLM E) is an enterprise-class solution
for quantum simulation that extends the capabilities of myQLM.
Avec Wolfram Mathematica les NoteBooks sont générés automatiquement à partir du calcul et de la programmation.
With the Jupyter notebooks, an open-source web application
that allows you to create and share documents that contain live code, equations, visualizations and narrative text
we prepare data cleaning and transformation, numerical simulation, statistical modeling, data visualization, machine learning and IA.
and With Binder, open those notebooks in an executable environment,
making your code immediately reproducible by anyone, anywhere.
https://gke.mybinder.org/
after enter your repository information by providing in the above form a URL or a GitHub repository that contains Jupyter notebooks,
as well as a branch, tag, or commit hash. Launch will build your Binder repository.
If you specify a path to a notebook file, the notebook will be opened in your browser after building.
A partir des travaux
sur la Trans-combinatoire et les Textures Prétopologiques et Quantiques et leurs Texturologies ainsi que les Processus Markoviens Prétopologiques
associés à l'Algèbre des Quinternions et à la Théorie des Sous-ensembles superposés et intriqués du Résualisme et de la Cybericité Sont préparés avec Mathematica, des outils d'IA et DeepLearning, classification multi-hierarchique et multi-paramétrique, avec représentation 2D et 3D interactives en temps réel par DataMining avec simulateur de vol dans les données en Réalité Virtuelle et Augmentée, et algorithmique de Trans-Combinatoire (3^(n-1) + 1 possibilités en parallel au lieu de 2^n), de Textures et Texturologies Quantiques Prétopologiques Relationnelles.
Le besoin d'une carte pour pouvoir voir le tableau d'ensemble est nécessaire.
Les modèles Markov State (MSM) sont une façon de décrire toutes les conformations (formes) qu'une protéine - ou d'autres biomolécules d'ailleurs - explore
comme un ensemble d'états (c'est-à-dire des structures distinctes) et les taux de transition entre eux.
Ils établissent également les propriétés de mouvement et d’énergie de la protéine en se repliant d’une forme à l’autre.
A partir de toutes ces informations, on observe les facteurs qui ont influencé le pliage, ce qui est particulièrement important si la protéine se déplie.
Une grande partie de la théorie sous-jacente à ces méthodes est assez ancienne, mais leur utilisation a été limitée par les défis inhérents à l'identification d'un ensemble raisonnable d'États.
Les MSM sont particulièrement utiles car ils facilitent la parallélisation entre de nombreux processeurs informatiques en permettant l'agrégation statistique de courtes trajectoires de simulation indépendantes.
Cela remplace la nécessité de trajectoires longues uniques et a donc été largement utilisé par les réseaux informatiques distribués tels que Folding@home et GPUGRID.
De plus, grâce à l'échantillonnage adaptatif, les MSM offrent un moyen d'accroître l'efficacité de la simulation sans introduire de biais ou d'approximations artificiels.
Beaucoup de progrès ont été fait en développant des méthodes de modèle d’état de Markov (MSM, Markov Stat Model, Model de Moor) pour analyser les données produitent avec l’aide de la communauté F@H.
Plusieurs membres du Groupe Pande incluant les Drs. Xuhui Huang et Gregory Bowman, ont développé MSMBuilder, un logiciel open-source utilisé pour construire, analyser et visualiser les MSM.
Depuis sa sortie en 2009, il a été téléchargé plus de 1 600 fois sur les cinq continents et a été utilisé dans au moins 40 publications à ce jour.
Formellement, les MSM sont une application spécifique d'équations maîtres d'espace discret paramétrées à partir de la simulation.
Elles se composent de deux parties :
- un système de partitionement de l'espace d'état X, généralement choisi pour diviser le système en un ensemble d'états métastables ;
- et une équation principale décrivant la cinétique sur X, représentée par une matrice de transition T ou une matrice de vitesse.
L'espace d'état et l'équation de base sont tous deux trouvés à partir de la simulation moléculaire.
La manière précise dont cela se fait varie considérablement.
A quoi ressemble un MSM (Markov Stat Model) ?
Entre les macroétats de la protéine :

MSM montrant 14 macroétats sur 2000 pour les MSM de la protéine NTL9.
Les États qui sont en meilleur équilibre sont dessinés plus grands et les transitions les plus probables
sont représentées par des flèches plus larges. Les protéines dépliées sont en rouge, et l'état natif est en vert. (Voelz et al.)
Les États qui sont en meilleur équilibre sont dessinés plus grands et les transitions les plus probables
sont représentées par des flèches plus larges. Les protéines dépliées sont en rouge, et l'état natif est en vert. (Voelz et al.)
Entre les transitions primaires d'une protéine :

MSM pour la protéine ACBP, illustrant certaines des transitions primaires. (Voelz et al.)
Qu'est-ce que l'échantillonnage adaptatif, et comment est-il lié aux MSM ?
Lorsque les chercheurs utilisent des ordinateurs pour étudier la dynamique conformationnelle des protéines (la façon dont la protéine change de forme au fur et à mesure de son pliage), l’approche conventionnelle pour la dynamique moléculaire non biaisée de tous les atomes est en deux étapes. D'abord, ils exécutent un ensemble de simulations, et ensuite, une fois les simulations terminées, ils analysent les données obtenues.
L'approche adaptative de l'échantillonnage Markov State Model implique de rompre ce paradigme en entrelaçant ces deux étapes. Au lieu de construire le modèle uniquement après la collecte des données, il est construit à la volée au fur et à mesure que les données sont générées. Une boucle de rétroaction peut ensuite être mise en place lorsque l'état actuel du modèle est utilisé pour éclairer l'avancement de nouvelles simulations.
Imaginez, par exemple, que vous exploriez un labyrinthe pour la première fois. Bien que vous n’ayez pas de carte, vous avez un GPS qui vous permet de suivre vos progrès et d’afficher les parties du labyrinthe que vous avez exploré. Une approche est de mettre le GPS dans votre sac et de marcher aveuglément .. renverser les murs .. aussi longtemps que possible. Une fois fatigué, vous sortez le GPS et analysez le chemin que votre trajectoire a suivi ; en regardant votre chemin sur le GPS, vous pouvez voir la structure du labyrinthe et avoir effectivement construit une carte. Malheureusement, vous remarquez que vous avez perdu beaucoup de temps dans différentes parties du labyrinthe. Au lieu de cela, la stratégie la plus intelligente est de regarder le GPS en marchant... pour essayer de construire votre carte du labyrinthe progressivement. En utilisant votre carte, vous pouvez identifier quand vous êtes "coincé" dans une certaine partie du labyrinthe, et éviter de redécouvrir des parties du labyrinthe que vous êtes sûrs d’avoir déjà découvertes.
À bien des égards, ces deux approches de l'exploration d'un labyrinthe sont analogues aux deux approches de la collecte et de l'analyse de simulations moléculaires.
En raison de la nature progressive de la construction du modèle à la volée dans l'approche d'échantillonnage adaptative, il est possible d'augmenter l'efficacité des simulations.
Comment créer un MSM à l'aide d'un échantillonnage adaptatif ?
Pour lancer un projet de simulation, nous devons d’abord choisir quelques conformations initiales (forme d’une protéine).
Les méthodes heuristiques utilisées jusqu’à présent, incluent l’exécution de simulations à haute température, l’utilisation de l’algorithme Monte Carlo de Rosetta et le choix asymétrique parmi les MSM apparentés de protéines similaires. (shooting off related MSMs of similar proteins)
Une fois un ensemble de conformations obtenu, chacune d'entre elles devient le point de départ de certaines simulations appelées ensemble "un Run" ou "Course" ou "Exécution"
A l'intérieur de chaque Course, de nombreuses trajectoires sont lancées, chacune appelée "un Clone".
Ainsi, tous les clones d'une course commencent à partir de la même forme protéique initiale.
Mais ils ont une vitesse initiale différente, c'est-à-dire que les atomes reçoivent une poussée initiale différente dans une direction ou une autre.
Les clones d'une exécution peuvent trouver des conformations supplémentaires, auquel cas les extrémités de la série et plusieurs autres exécutions sont démarrées à partir d'elles.
Ce processus se poursuit avec beaucoup de Runs qui se ramifient à d'autres conformations, fusionnant peut-être ensemble à une forme commune avec d'autres Runs.
Au final, un modèle ayant des dizaines de milliers de conformations différentes, (téraoctets de données !) ayant :
- toutes les formes et les états d'énergie que la protéine peut prendre pendant son repliement vers son "état natif",
- les chances de toutes les transitions se produisant,
- et combien de temps il faut à la protéine pour terminer une transition d'une conformation à une autre.
Plus important encore, l'identification des endroits où les protéines se replient et se coincent, mène ensuite à plus de recherches et de modèles sur la façon d'empêcher cela de se produire.
Plus il y a d'ordinateurs participants, plus vite il est possible de compléter le Modèle d'État de Markov.
Qu’est-ce que les numéros PRCG ?
Les unités de travail sont étiquetées avec quatre numéros distincts dans le format : Project (Run, Clone, Generation), Projet (Exécution, Clone, Génération).
Donc si le projet est la protéine à l'étude :
- un Run est une simulation lancée à partir d'une conformation particulière,
- et Runs contient de nombreux clones qui ont des vitesses initiales différentes.
Bien que Folding@home traite de nombreux projets, exécutions et clones différents en même temps, les clones eux-mêmes sont de nature série.
Ils doivent être simulés du début à la fin, mais il serait peu pratique pour un ordinateur d'en terminer un seul.
Au lieu de cela,
Votre ordinateur reçoit un morceau de clone. La pièce est identifiée en utilisant le numéro Génération (Gen).
Un ordinateur démarrera avec la Génération 0, et quand il finira, à un autre ordinateur sera donné la Génération 1, etc. Le Gen 1 ne peut démarer tant que le Gen 0 n'aura pas fini, et il peut y avoir des centaines de Gens. C'est pourquoi les unités de travail ont des délais et pourquoi la vitesse est si importante.
Pourquoi cette approche est-elle particulièrement utile ?
Cette approche peut être puissante car non seulement elle est très modifiable pour l'informatique distribuée, mais les ressources informatiques disponibles peuvent être utilisées plus efficacement.
Une protéine passe la plupart de son temps de pliage "coincée" dans une position énergétiquement favorable,
avec des transitions - les processus en grande partie intéressants - n'ayant que rarement lieu.
De même, toute simulation simple du pliage de protéines perdra également du temps précieux à produire des données avec peu d'information.
Cependant, en utilisant le concept d'échantillonnage adaptatif, le modèle peut déterminer quand la simulation est bloquée,
puis réinitialiser de nouvelles simulations à partir de zones potentiellement plus fructueuses, en évitant le processus inutile de ré-exploration des zones déjà bien comprises.
Les MSM ont été comparées à des méthodes de simulation plus traditionnelles comme les trajectoires de pliage très longues du superordinateur Anton, à un MSM construit à partir des mêmes données de pliage. Bien que la MSM ait "découpé" la simulation en un tas de trajectoires courtes, il a été capable de reproduire très bien leurs simulations.
De plus, l’approche des MSM a révélé de nouvelles idées sur le processus de pliage (une nouvelle voie de pliage) qui manquait dans l’approche plus traditionnelle d’ANTON.
Quelles sont les applications de ces techniques ?
Les MSM et l'échantillonnage adaptatif ont été utilisés pour étudier le pliage des protéines (1-8),
la dynamique fonctionnelle (8-11), la liaison des ligands (11-14) et les interactions protéine-protéine (15).
- Jayachandran G, Vishal V, & Pande VS (2006) Using massively parallel simulation and Markovian models to study protein folding: Examining the dynamics of the villin headpiece. Journal of Chemical Physics 124:164902.
- Bowman GR, Beauchamp KA, Boxer G, & Pande VS (2009) Progress and challenges in the automated construction of Markov state models for full protein systems. Journal of Chemical Physics 131(12):124101.
- Noe F, Schutte C, Vanden-Eijnden E, Reich L, & Weikl TR (2009) Constructing the equilibrium ensemble of folding pathways from short off-equilibrium simulations. Proceedings of the National Academy of Sciences of the USA 106(45):19011-19016.
- Bowman GR & Pande VS (2010) Protein folded states are kinetic hubs. Proceedings of the National Academy of Sciences of the USA 107(24):10890-10895.
- Beauchamp KA, Ensign DL, Das R, & Pande VS (2011) Quantitative comparison of villin headpiece subdomain simulations and triplet-triplet energy transfer experiments. Proc Natl Acad Sci USA 108:12734-12739.
- Bowman GR, Voelz VA, & Pande VS (2011) Atomistic folding simulations of the five-helix bundle protein (6-85). Journal of the American Chemical Society 133(4):664-667.
- Voelz VA et al. (2012) Slow unfolded-state structuring in Acyl-CoA binding protein folding revealed by simulation and experiment. Journal of the American Chemical Society 134(30):12565-12577.
- Lane TJ, Bowman GR, Beauchamp K, Voelz VA, & Pande VS (2011) Markov state model reveals folding and functional dynamics in ultra-long MD trajectories. Journal of the American Chemical Society 133(45):18413-18419.
- Yang S, Banavali NK, & Roux B (2009) Mapping the conformational transition in Src activation by cumulating the information from multiple molecular dynamics trajectories. Proc Natl Acad Sci USA 106(10):3776-3781.
- Morcos F, et al. (2010) Modeling conformational ensembles of slow functional motions in Pin1-WW. PLoS Computational Biology 6(12):e1001015.
- Bowman GR & Geissler PL (2012) Equilibrium fluctuations of a single folded protein reveal a multitude of potential cryptic allosteric sites. Proc Natl Acad Sci USA 109(29):11681-11686.
- Silva DA, Bowman GR, Sosa-Peinado A, & Huang X (2011) A role for both conformational selection and induced fit in ligand binding by the LAO protein. PLoS Computational Biology 7(5):e1002054.
- Buch I, Giorgino T, & De Fabritiis G (2011) Complete reconstruction of an enzyme-inhibitor binding process by molecular dynamics simulations. Proc Natl Acad Sci USA 108(25):10184-10189.
- Held M, Metzner P, Prinz JH, & Noe F (2011) Mechanisms of protein-ligand association and its modulation by protein mutations. Biophysics Journal 100(3):701-710.
- Levin AM et al. (2012) Exploiting a natural conformational switch to engineer an interleukin-2 ‘super-kine.’ Nature 484(7395):529-533.
Markov State Model (MSM) construction et validation
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3462454/
The MSMBuilder33 software was used to build MSMs for ACBP under folding conditions (0M GuHCl, 330K simulations) and unfolding conditions (0.6–1.0 1M GuHCl, 370K simulations).
We found that a 20,000-microstate decomposition yielded a good balance of state connectivity and adequate transition sampling.
Conformations were clustered using a subset of 258 atoms (backbone N, Cα and C);
20% of the data was used to generate an initial clustering,
and the remaining 80% of the data was assigned to the generators.
The 20,000-microstate model was used for predicting experimental observables, while a 2000-macrostate MSM obtained by kinetic-based lumping 34 was used to analyze the distribution of folding pathway fluxes from unfolded to folded states.
Transition probabilities Tij of transitioning from state i to state j (within a lag time τ) are estimated by counting the number of transitions nij observed between time t and t+τ, and normalizing by rows: Tij = nij/(Σj nij).
To enforce detailed balance, is done the symmetrization of the forward and backward counts as : (nij+nji)/(Σj nij+nji).
Artifacts from symmetrization are mostly limited to transitions with very few counts (and hence low populations that have negligible effects).
Sliding-window counts were used to alleviate finite-sampling errors.
To validate the robustness of these assumptions in estimating transition rates, importance sampling is performed of the posterior distribution of 2000-macrostate transition matrices, using a reversible conjugate prior for Markov chains as described in 35.
Are generated ~5000 Markov chain realizations (samples of transition counts ñij, with no sliding window used; calculations are limited by storage space), from which expectation values (mean and variance) of equilibrium populations pi ∝ (Σj ñij) were calculated.
The expectation equilibrium populations calculated using the reversible prior were very similar to the symmetrization results (Supplementary Fig. S7e,f).
For example, the native macrostate population (pnat) using this procedure was 28.13% +/− 0.069%,
whereas the transition matrix constructed directly from from sliding-window counts yielded pnat = 30.3%, a discrepancy of only ~0.07 kT.
A lag time of τ=20 ns was determined to be suitable by building a series of MSMs at different lag times to find a region where the spectrum of implied timescales 36, 37
τi = −τ/ln(λi) are relatively insensitive to lag time.
To check the accuracy of the MSM, we compared average inter-residue distances over time (17–86, 1–86 and 17–50) seen in the trajectory data, to predictions from the MSM, and found reasonable agreement (see SI section B.1).
While the implied timescales become accelerated after lumping (it is difficult to achieve a perfect separation of timescales), distributions of folding pathway fluxes remain mostly intact for analysis.
A Bayesian inference model described in 38 was used to estimate Arrhenius barriers ΔGij separating microstates and macrostates.
Committor (pfold) values and mean first passage times were computed for each macrostate using methods described in 37, 39.
The pfold values we compute for MSM macrostates are defined as the probability of reaching the native macrostate before the unfolded extended-chain macrostate.
Transition Path Theory (TPT) 40–42 was used to calculate pathways of reactive folding flux, using a modified “greedy backtracking” algorithm (see SI section B.2).
MSM equilibrium population vectors were calculated from the largest eigenvector of the transition matrix, i.e. from peq = peqT.
Macrostate free energies Fi were calculated from MSM equilibrium populations pi as Fi = −kT log pi at room temperature.
The free energy of folding as a function of the kinetic reaction coordinate pfold was calculated as F(pfold) = −kT log Z(pfold) where,
Z(pfold) = Σi χipi where χi is a bin indicator variable for bins with left edges
pfold = 0, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.6, 0.7, 0.8, 0.9, 0.95.
Master Equation formalism
The continuous-time master equation describing the microstate dynamics is dp/dt = pK,
where p is the vector of state populations, and K is a 20,000 × 20,000 matrix of rate coefficients,
related to the discrete-time transition probability matrix by T = exp(τK)
The solution of the master equation is
p(t) = ΣnψLn[ψRn · p(t = 0)] exp(λnt) = Σn pn(t),
where ψLn, ψRn, λn are the left and right eigenvectors and eigenvalues of K, respectively.
The kinetics can thus be described as a superposition of exponential relaxation modes pn(t)
at implied timescales τ*n = −λn−1, each with amplitude an = [ψRn · p(t=0)].
MSM predictions of observables
Predicted values of observables over time were computed as F(t) = p(t) · f, where p(t) is a vector of state populations over time,
and f is a vector of observables values for each microstate.
Uncertainty estimates were propagated assuming statistical independence of each state.
For some observables, time courses were obtained by discrete propagation of the transition probability matrix T, using p(t+τ) = p(t)T.
For others, p(t) was calculated from the 1000 slowest relaxation modes of the master equation solution.
RMSD pseudo-trajectories were calculated using a simple Monte Carlo algorithm to generate a trajectory of (20 ns) microstate jumps,
and selecting at random (uniformly) a simulation snapshot to report observables at each time step (see SI section B.3 for more examples).
Predictions of FRET observables over time were computed with special corrections for FRET probe linkers not present in the simulations (see SI section B.4),
and corrections for native state stability (see below).
Trp-Cys quenching rates and intramolecular diffusion coefficients for T17C-W58 and W58-I86C were predicted using methods described in 25 from simulated distributions of intramolecular Trp-Cys distances P(r) calculated from simulated unfolded ensembles (330 K, 0 M GuHCl and 370 K, 0.6–1.0 M GuHCl, starting from extended
and coil states, snapshots taken after 1 µs), where r is the distance between side-chain centroids (see also SI section A.5).
Intramolecular diffusion coefficients D were computed from trajectory data,
by fitting the mean-squared displacements of Trp-Cys distances over time in blocks of 50 ns (sampled in 1-ns intervals), as described previously.
Correcting predicted FRET (Förster resonance energy transfer) values for native-state stability
A consequence of symmetrization of the transition probability matrix is that the equilibrium populations are proportional to the total number of observed counts : pi ∝ (Σj nij).
Because of this, the MSM predicts an equilibrium distribution of states with ~2:1 unfolded vs. folded populations, even under folding conditions.
To correct predicted observables, the FRET values are compute by subtracting the equilibrium unfolded-state component of the signal (i.e. the simulated unfolded state is “invisible”).
The stationary state peq = (ncoil + next + nnat)/(Ncoil + Next + Nnat) is the (normalized) number of counts observed in the trajectories, where ncoil, next, and nnat are the vectors of observed microstate counts for simulations initiated from coil, extended and native states, respectively,
and N = Ncoil + Next + Nnat is the total number of counts observed in all simulations.
The discrete-time transition matrix is propagated as described above to get populations over time, and calculate FRET using a modified projection operator S′:
S'(p) = (N/Nnat) · [S(p)−S([next + ncoil]/N)]
This projection operator has the property that as t→∞, S'(p(t→∞)) = S(nnat/Nnat).
This correction for the FRET predictions is used in Figure 2d, setting the starting configuration p(t=0) to a single microstate corresponding to the extended state. A caveat of this approach is that negative FRET values may be obtained at very early times, when initial popultaions are from unfolded states. For all case, this effect only occurs for t < 1 µs, faster than the time resolution of the mixer experiments with which comparisons are making.

Folding kinetics of hydrophobic core mutants of ACBP 17–88 measured in an ultrafast microfluidic mixer. (a) Mutations F26A and Y31N (shown to disrupt unfolded-state structure in smFRET experiment) decrease the relaxation amplitudes of the fast kinetic phase, but do not significantly affect relaxation rates (see Supplementary Figure S11 and SI section B.4 for fitting details). Burst-phase amplitudes occurring within the mixing time (< 4 µs) are evidence of residual structure already formed at early times. (b) Disruption of residual structure induced by chemical denaturant, exemplified by the F26A variant. (c) Average FRET-trajectories of the W55F variant measured in separate mixing experiments out to ~800 µs. Five independent measurements, normalized to initial and final asymptotic values, were averaged, with the error bars representing the standard deviations of this average. (d) MSM predictions of FRET time courses (see below, Methods) show kinetic time scales in qualitative agreement with experiment. Confidence intervals (thin lines) reflect uncertainty in R0 and probe distances (see SI).
Results
Experimental evidence for a highly structured denatured state
To study the denatured-state structure of ACBP under a wide range of experimental conditions, smFRET studies45,46 were performed. Pairs of Cys residues were engineered into the ACBP sequence (wild type ACBP is Cys-free) that were subsequently labeled with a FRET dye pair (Alexa488/Alexa647). The FRET pairs were positioned such that they report on distance changes within discrete substructures of the four-helix bundle topology (Figure 1a, top).
For example, labeling at position 1–68 reports on distance changes within the first three N-terminal helices, while labeling at positions 17–88 reports on changes in the three C-terminal helices. Likewise, ACBP 1–40 reports predominantly on the integrity and interaction of helix 1 (previously reported to be flexible and engaging in little long-range residual structure4), while ACBP 1–88 probes end-to-end distance changes (SI section A.3 for additional information).
These FRET-pair variants contained an additional, highly destabilizing W55F mutation to populate the denatured subensemble at very low denaturant concentrations. Comparison with wild type ACBP suggests that the W55F mutation does not significantly perturb residual structure in denatured state, at least under conditions where both mutant and wild type populate the denatured state to measurable quantities (0.8–6 M GuHCl) (Supplementary Fig. S1a).

Figure 1
Unfolded-state structure studied by smFRET experiments at equilibrium. (a) Single molecule FRET histograms measured with site-specifically labeled ProL (grey, reference), and four ACBP variants (blue, red, orange, green) at various denaturant concentrations.
(b) Unfolded-state FRET-efficiencies versus denaturant concentration for each variant, shown with the ProL reference
(c) FRET-based random coil Rg estimates for ACBP revealing non-uniform compaction, and compaction to a greater extent than the ProL random-coil reference. Rg values were normalized to the Rg estimate of ACBP 17–88 by multiplying by the Flory scaling factor (see SI section A.4).
(d) Mutant Y31N produces a significant expansion of the unfolded state, indicating a disruption of long-range structure. (Data for other mutants shown in Supplementary Figure S1.)
FRET-efficiency histograms of the four FRET-pair mutants of ACBP exhibit folded (high-FRET) and unfolded (low-FRET) subpopulations that coexist at intermediate denaturant concentration, as expected for a thermodynamic two state folder with a free energy barrier separating folded and unfolded subpopulations (Figure 1a, bottom).
Mean FRET-efficiencies of the folded and denatured subpopulations were extracted from Gaussian fitting of the histograms. The mean FRET-efficiencies of the denatured subpopulation of each FRET-pair mutant at a particular denaturant concentration are plotted in Figure 1b, together with the mean-FRET efficiency of a highly destabilized and constitutively unfolded triple-Ala variant of ProL (see SI section A.1 for details), that serves here as a pseudo-random coil reference.
Clearly, all four interresidue distances of ACBP probed by smFRET experience significantly larger contractions than the single distance probed in the ProL reference, particularly below 3 M GuHCl, suggesting a compact ensemble of structures under conditions that favor folding.
To compare the mutant effects more quantitatively and to better connect the experimental results with simulation predictions, the FRET-efficiencies are next converted into radii of gyration (Rg), which were then normalized to identical chain length (88 residues) by multiplication with the Flory scaling factor (Figure 1c, SI section A.2 for additional information).
Under strongly denaturing conditions (> 3 M GuHCl), all five proteins show (within error) identical polymer behavior, suggesting that under those conditions, chain contraction is sequence-independent and probably unspecific (see SI section A.3).
Below 3 M GuHCl, however, a significant shortening of each of the four ACBP distances is not only observed beyond that measured in the ProL reference (suggesting acquisition of compact residual structure beyond that seen in the ProL random coil), but also significant differences among the ACBP distances themselves, demonstrating non-uniform compaction. The 1–40 distance exhibits the weakest contraction, which is consistent with previous reports4,47 that helix 1 is more flexible and engages in less residual structure than the remaining three helices.
The largest distance change is experienced by 17–88, with 1–68 exhibiting a behavior in between 1–40 and 17–88. The latter observation is noteworthy, as the interdye distance in 17–88 (72 residues) and 1–68 (68 residues) is almost identical, the only difference being that 17–88 includes the structured C-terminal helix (45 % folded in isolation), while 1–68 includes the weakly structured and more flexible N-terminal helix.
To provide further evidence for residual structure in denatured ACBP, additional mutants were made in the 17–88 FRET-pair context by replacing large, hydrophobic residues that engage in long-range residual structure in folded ACBP (F5A in helix 1, F26A, I27A, Y28A, Y31N in helix 2, and W55L in helix 3; SI section A.3 for additional information). Indeed, for the non-conservative Y31N mutant, a significant perturbation of residual structure (Figure 1d) is observed, a result that is also predicted by reweighting of the simulated unfolding ensembles (Figure 6c, Supplementary Figure S2). Interestingly, even though the F5A mutation perturbs the same long-range interactions as the Y31N in the folded protein, it doesn’t affect denatured-state structure measureably. Perturbation of native-like structure in the denatured ensemble is thus likely not to be the cause of the disruptive effect of the Y31N mutant.
Significant denatured-state expansion in the F26A, I27A and Y28A mutants (Figure S1) is not see, which is perhaps surprising, given that the mutated residues F26, I27, Y28 and Y31 are all positioned in helix 2, and are separated by less than two helix turns in the folded protein. This could simply be because Y31N is more disruptive than the other, more conservative, alanine mutations. Another, more provocative explanation, is that these differential disruptive effects are reporting the presence of specific long-range helix-helix contacts in denatured ACBP. Such an interaction was first postulated by Poulsen and co-workers for helix 2 and helix 4 from spin-sensitized NMR experiments, a hypothesis that is supported by more recent molecular dynamics simulations that reveal similar contacts persisting in acid-denatured ACBP (pH 2.3), i.e. conditions where ACBP is > 99% unfolded. Such long-range interaction might be favored by the amphipathic nature of the two heices and the high helical propensity of helic 4 (60% folded in isolation) that may act as a hydrophobic docking site for helix 2. Indeed a helical wheel plot suggests that residue Y31 would be positioned right in the center of the putative hydrophobic helix interface, while residues F26, I27 and Y28 would adopt more peripheral positions (Supplementary Figure S1b).
It is therefore plausible that a Y31N mutation would exert a more perturbing effect. As the rate-limiting step for folding is the formation of side chain contacts between helices 1, 2 and 4, long-range contacts between helices 2 and 4 in the denatured state might be advantageous for barrier-limited folding1.
A much more extensive mutational analysis, however, is required to fully support this model.
Surprisingly slow formation of unfolded structure
The hypothesize that the ~80 µs kinetic phase seen previously7 might reflect a gradual (microsecond timescale) collapse to a heterogeneous ensemble of unfolded, yet highly compact structures, rather than the formation of a classical folding intermediate.
Strong support for this hypothesis comes from non-equilibrium FRET experiments measured with the F26A, Y31N and W55F mutants of ACBP 17–88 in an ultrafast laminar-flow mixing device.
The FRET-trajectories of the three mutants, measured upon refolding of denatured protein (6 M GuHCl) into refolding buffer (0 M GuHCl), are biphasic, with a submicrosecond burst phase occurring within the mixing time of the mixer (< 4 µs), followed by a fast, kinetically resolvable relaxation process occurring on the ~100 µs timescale (Figure 2a). The W55F trajectory (Figure 2b, red) is best fit by either a single exponential (relaxation time scale = 48 ± 4 µs), or a stretched-exponential (relaxation time scale = 46 ± 3 µs; β = 0.80; see SI section A.4 for further details on curve fitting). Additional measurements for the W55F variant at both high and low flow rates were made in separate mixing experiments to extend the time range of FRET-trajectories to ~800 µs (Figure 2c). The results (after normalization to account for minor differences in detection efficiencies) agree well with the shorter trajectories after 20 µs (see SI section A.4). The full time course of FRET vs. time predicted by the MSM (which does not predict a stable folding intermediate, Figure 5) seems to qualitatively reproduce the ~800 µs FRET-trajectory (Figure 2d). The simulated dynamics predicted by the MSM are slightly faster (~1–10 µs). This agreement with experiment is reasonable considering potential systematic error from forcefield and rate estimation effects (see below).

Figure 5
Markov State Model (MSM)-based simulation of ACBP folding in all-atom detail on the tens of millisecond timescale.
(a) Folding pseudo-trajectories generated from the MSM, projected onto a single degree of freedom such as the RMSD-Cα to the native crystal structure, suggests cooperative folding to the native state via a simple two-state mechanism, near the millisecond timescale. The MSM, however, is a complex network of metastable states, and the full picture of the folding dynamics is predicted to be more complex.
(b) Shown are the 15 highest-flux folding pathways bridging the extended and native states in a 2000-macrostate MSM, as calculated by Transition Path Theory (TPT)41. Line thicknesses are proportional to pathway folding flux (on a log-scale). Circled are the macrostates corresponding to the native and near-native state identified by Teilum et al.2
(c) Free energy vs. pfold (a kinetic reaction coordinate defined as the probability of reaching the native state versus the extended state), plotted for each macrostate (black dots), shows a highly diffuse network of unfolded states, yet a simple basin structure in a 1D projection (red line). Gray edges represent the network of fluxes shown in (b).
(d) Average inter-residue contact propensities calculated from unfolded-state simulations corresponding to ~1M GuHCl (see Methods for details on the conversion of temperature into denaturant concentration), taken after 5 µs, show long-range contacts between helices 2 and 3, and helices 2 and 4. Contours show free energies of contacts (units kT) compared to a reference normalized by loop length. Blue squares denote native contacts.
The slow, barrier-limited folding transition occurring on the ~10 ms time scale, and accounting for the remaining 5–10 % of the expected FRET amplitude change upon folding, cannot be resolved at the high flow rates employed in this study. However, previous laminar-flow mixing studies at substantially slower flow rates and different mixer design revealed an additional slower phase with a rate constant (~ 9 ms) almost identical to the rate constant reported from Trp-fluorescence detection7, thus ruling out a major perturbation of the energy landscape by the bulky fluorophores.
Increasing the denaturant concentration in the refolding buffer results in a nonlinear decrease of the amplitude of the kinetically resolvable relaxation process (Figure 2b). The relaxation rates of the three mutants, obtained from single exponential fits and rate spectra analysis (see below) of the FRET-trajectories, agree within a factor of 2.5 and are only weakly affected by denaturant, as found previously7. Interestingly, mutants Y31N and F26A result in lower dead-time collapse amplitudes than the W55F mutant, indicating that there is already long-range residual structure developing within the first few microseconds of refolding. This hypothesis is supported by earlier experiments and simulations that show that contacts between helices 2 and 3 persist at moderately high denaturant concentrations (3 M GuHCl)4, and our own simulation predictions (see below) that similar interhelical contacts persist at moderately denaturing temperature (370 K, corresponding to 0.6–1.0 M GuHCl) (Supplementary Figure S3). It is therefore plausible that helix 2–helix 3 contacts form early in the folding process while helix 2-helix 4 contacts (which form at lower denaturant concentrations4) form later. Similar fits for for F26A and Y31N yield ~90 µs and ~120 µs, respectively.
Extrapolations of the (normalized) asymptotic FRET efficiencies estimated from non-equilibrium mixing are founded, agreed within experimental error with the FRET-efficiencies of the denatured subpopulation of ACBP inferred from smFRET experiments at equilibrium (Figure 3). Such good agreement between normalized transient and equilibrium FRET efficiencies is difficult to rationalize in the framework of a folding intermediate (see Discussion).

Figure 3
Comparison of relative
FRET-efficiencies for the denatured subpopulation measured by
equilibrium smFRET (circles) and the asymptotic FRET-efficiency of the
time-resolvable microsecond kinetic phase measured by ultrafast
laminar-flow mixing (triangles). A comparison of relative FRET efficiencies was necessary to account for minor differences in detection efficiencies between the microscopic setups used for the smFRET and ensemble mixing experiments and the presence of donor-only species in the ensemble mixing experiment that were digitally removed in the smFRET experiments. For the smFRET experiments, raw FRET efficiencies of the denatured subpopulation at a particular denaturant concentration were normalized to the difference in FRET efficiency between the folded subpopulation at 0 M GuHCl, and the FRET efficiency of the denatured subpopulation at 6 M GuHCl. For the ensemble mixing experiments, raw asymptotic FRET efficiencies for the microsecond phase at a particular denaturant concentration were normalized to the difference in FRET efficiency of the denatured protein at 6 M (unfolded baseline in Fig. 3a, main text) and the folded protein at 0 M (folded baseline in Fig. 3a, main text). Note that some asymptotic FRET values are not shown: W55F (6 M to 3 M), Y31N (6 M to 1.5 M) and Y31N (6 M to 3 M); these traces were poorly fit by a single-exponential.
Trp-Cys quenching studies suggest slow intramolecular diffusion in the denatured state
To further probe unfolded-state structure and dynamics, Trp-Cys contact quenching studies were performed. These studies measure the time-resolved decay of the excited triplet state of tryptophan, and its quenching by cysteine in the unfolded state, to give insight into intramolecular dynamics in the unfolded state48. Studies were performed for two single-cysteine mutants of the same W55F variant of ACBP which were also used for the smFRET and fast mixing experiments.
The first mutant contains a single Cys at position 17 and probes intramolecular diffusion within the T17C-W58 loop that comprises helices 2 and 3 and the long connecting loop that connects the two helices.
The second mutant contains a Cys at the C-terminus and reports on chain dynamics in the W58-I86C loop, i.e. on dynamics within the two C-terminal helices.
Measurements were performed at equilibrium from 1 M to 6 M GuHCl, as well as in a fast mixer49 which diluted denaturant from 5 M to 0.2 M and 0.8 M GuHCl (0.8 M GuHCl only for T17C-W58) in order to observe intramolecular diffusion before barrier-limited folding.
A previous study has shown good agreement between equilibrium and mixer measurements at the same denaturant concentration49. The observed quenching rates kobs are modeled as resulting from a combination of a reaction-limited rate, kR, and diffusion-limited rate, kD+, which can be extracted by varying viscosity and temperature independently.
An effective diffusion coefficient can be determined from the measured rates and simulated Trp-Cys distance distributions, using methods described previously25 (see SI section A.5). Within the mixer, the observed quenching rate slows down within the mixing time (Figure 4a). The slope of a linear fit of 1/kobs vs. viscosity for W58-I86C gives kD+ = 1.18 ± 0.41 × 105 s−1 at η=1 cP (Figure 4b).

Figure 4
Trp-Cys quenching studies of ACBP report slow unfolded-state intramolecular dynamics under folding conditions. (a) Observed quenching rates vs. time for loop W58-I86C in a fast mixer after diluting from 5 M to 0.2 M GuHCl, shown with an exponential fit to the data.
(b) Linear dependence of W58-I86C quenching times (T=23C) with viscosity at ~1.4 ms, shown with a least-squares linear fit, R2 = 0.729. (T17C-W58 times are not shown as they are too slow to accurately measure.) (c and d) Reaction-limited kR (filled) and diffusion-limited kD+ (open) vs. [GuHCl] for
(c) W58-I86C and
(d) T17C-W58 loops. Red circles denote kR predictions from simulation data, and the dotted line reflects a lower limit of D at 0.2 M (see SI).
(e) Intramolecular diffusion coefficients extracted from the W58-I86C data using SSS theory (see SI section B.4), and the red circle marks D calculated from simulated mean-squared displacements vs. time at 300K (0 M GuHCl).
Qualitatively, the intramolecular dynamics of ACBP exhibits a pattern similar to previously studied proteins (protein L, protein G): Decreasing the denaturant concentration induces a chain compaction, which increases kR and decreases kD+, suggesting less diffusivity (Figures 4c,d). For both loops, kR and kD+ cross at ~1.5 M GuHCl, near the denaturation midpoint, behavior seen previously for protein L, although the midpoint is much lower for ACBP. For the T17C-W58 loop, kD+ becomes too slow to accurately measure (< 4×104 s−1) suggesting this loop is less diffusive than the W58-I86C loop, consistent with the pattern of long-range contacts seen in simulation.
Intramolecular diffusion coefficients at low denaturant concentrations, estimated using experimental rates and a simulated Trp-Cys distribution, were estimated to be ~6 × 10−9 cm2/s, suggesting that the unfolded state in the absence of denaturant is highly collapsed and slowly diffusing, though the level of diffusivity may vary across the chain (Figure 4e).
Significantly, a independent estimate of the diffusion coefficient entirely from simulation gives the same estimate (red point in Figure 4e), showing agreement between simulation and experiment. This result is ~10 times higher than observed for protein L49, despite the fact that it is more compact (see also Figure 1b). The diffusion coefficient decreases dramatically below the denaturation midpoint. Along with the crossing of kR and kD+, and the dramatic increase in FRET from single molecule studies at the denaturant midpoint, this behavior shows the unfolded chain becomes compact and undergoes slow dynamics as the probability of folding becomes significant.
A Markov State Model of ACBP folding predicts a complex network of metastable states
Recently, discrete-state master equation or Markov state models (MSMs) have had success at modeling long-time statistical dynamics11,12,42,43,50.
In these kinetic network models, metastable states are identified such that conformational transitions within each state are much faster than transitions between states, so that the process can be considered to be Markovian51.
The transition rates between states are estimated from Molecular Dynamics (MD) simulations. If the model can self-consistently reconstruct the statistical dynamics of the trajectories it was constructed from, and if it obeys the Markov property, it can be used to simulate the statistical evolution of a non-interacting ensemble of molecules over much longer timescales than the lengths of the individual trajectories from which it is constructed (validation efforts described in Methods).
MSM dynamics can be directly compared with bulk experimental data by computing observables from the predicted state populations over time, as expectation values averaged over each state (see Methods).
MSMs is builded from over 30 milliseconds of atomistic MD simulation trajectories33 (distributions of trajectory lengths are shown in Supplementary Figure S4), for both folding conditions (330 K, 0 M GuHCl) and unfolding conditions (370 K, 0.6–1.0 M GuHCl). The native state is stable at 330 K, with a ~3 Å RMSD-Cα to the crystal structure (PDB code 1hb6) maintained after 1 µs. Trajectories from the 330 K ensemble, initiated from folded and unfolded conformations, were used to construct a 20,000-microstate MSM. The continuous-time master equation solution of the microstate kinetics gives a spectrum of implied timescales (see Methods), with the slowest implied timescale corresponds to the overall folding time. The folding time predicted from the MSM is ~3 ms, comparable to the ~ 9 ms experimental folding time (Supplementary Figure S5).
Although no complete folding events were observed in any one trajectory, the network of microstates is fully connected by the many unfolding and partial re-folding events simulated (Supplementary Fig. S6).
The lowest-free energy microstate contains the native state, and has a cluster center with RMSD-Cα to the crystal structure of ~0.6 Å (Supplementary Fig. S7). The average RMSD-Cα between pairs of conformations in each microstate (i.e. the microstate radius) is 6.89 ± 1.47 Å, slightly larger than previously MSM models of folding (for example, a 100,000-microstate MSM built from simulations of NTL9 (1–39)11 had an average microstate radius of ~4.5Å), due to the larger size of ACBP (86 residues) and the correspondingly larger accessible conformational volume.
For comparison, an MSM is builted from the 370 K data. The average microstate radius in this model was 8.40 ± 1.88 Å. The lowest free-energy microstate still contains the native state, although the relative free energies of the other microstates are lower (Supplementary Fig. S7). For the discussion below, we will restrict our attention to the 330 K MSM constructed for folding conditions.
Macroscopically, the MSM predicts cooperative transitions between the folded and denatured subpopulations on the millisecond timescale, consistent with experiment (Figure 5a). Microscopically, however, the model is considerably more complex. Consistent with recent simulation and experimental studies showing kinetic heterogeneity52, our MSM model predicts a striking heterogeneity of metastable states and folding pathways existing on the mesoscopic scale. MSMs of protein folding for several proteins have previously been reported to have a hub-like network of states around the native state12,38,53. We report a similar hub-like structure for ACBP, consistent with these findings. Mean first passage times (MFPTs) to the native microstate are three orders of magnitude faster than MFPTs to non-native states (Supplementary Figure S8).
A 2000-macrostate MSM obtained from the 20,000-microstate MSM by kinetic-based lumping34 was used to analyze the distribution of folding pathway fluxes from unfolded to folded states. The highest-flux pathways connecting a fully extended state to the native state show contact formation between helices 1 and 4 that are coupled to the folding transition, consistent with phi-value analysis by Kragelund et al1 (Figure 5b). Furthermore, our model predicts a near-native state with a displaced helix 3, corresponding well to a near-native intermediate identified by Teilum et al2.
A surprising feature predicted by the MSM is the absence of a single well-defined folding intermediate postulated in earlier kinetic studies. The free energy of folding as a function of the kinetic reaction coordinate pfold was calculated as F(pfold) = −kT log Z(pfold) where, Z(pfold) was estimated at 300K as the sum of equilibrium macrostate populations for binned values of pfold (see Methods). The free energy diagram shows two low-free energy basins corresponding to the unfolded and folded state, but no other intermediates along the reaction coordinate. Preceding the main folding barrier is a highly diffuse network of compact metastable states with residual unfolded-state structure (Figure 5c). These states contain both native and non-native contacts, consistent with the predictions of past simulations11 and a recent analytical model of hub-like folding networks54.
Unfolded-state compaction in simulated ensembles
Simulated unfolded-state ensembles were generated from trajectories starting from fully extended and random-coil conformations, and used to compute several observables directly comparable with experiment. The extended ensemble shows significant chain compaction by ~100 ns (see SI section B.5), reaching a radius of gyration (Rg) by ~5 µs similar to the coil ensemble, although slightly less compact (Figure 6a), in agreement with previous unfolded-state simulations25. A polymer-theory of the coil-globule transition fits the simulated Rg values well for simulated ensembles at different temperatures (Figure 6a, see Methods, SI section C). While these fits show unrealistically high melting temperatures (as found previously25), they are useful in obtaining transfer free energies per monomer as a function of simulation temperature, which can then be used to find experimental denaturant concentrations where ACBP exhibits a similar extent of chain compaction (see Methods). The comparison of simulated versus experimental Rg obtained by smFRET at the calibrated denaturant concentrations compares favorably (Figure 6b).
To model the sequence-dependent unfolded-state expansions measured by smFRET, a free energy perturbation approach to reweight conformations from simulated unfolded-state ensembles. By using a sufficiently coarse-grained and smooth potential to model sequence perturbations (see Methods; SI section B.6), accurate reweighting was possible using twenty thousand snapshots from simulated unfolded-state ensembles (taken after 5 µs). We calculated expectation values of interresidue distance 17–86 for the simulated wild-type (86-residue) sequence, as well as several mutant sequences characterized by smFRET. Our results generally agree with changes in end-to-end distances observed by smFRET: mutation Y31N is predicted to have the largest disruption of unfolded-state structure, as seen experimentally (Figure 6c). The relatively coarse resolution of our perturbation method, along with effects not accounted for in the model (such as the speculated amphipathic helix packing between helices 2 and 4; see above), are likely the main source of disagreement.
Unfolded-state structure in simulated ensembles
Interresidue contact propensities after 5 µs were calculated for unfolded-state ensembles generated from extended starting structures (see Methods). Similar patterns of unfolded-state structure were found in the low-temperature (330 K, 0 M GuHCl) and high-temperature (370 K, 0.6–1.0 M GuHCl) simulated ensembles. Significant helical secondary structure is predicted for residues in helix 1, 2, and 4 (as calculated by DSSP55, Supplementary Figure S9), in a pattern consistent with chemical shift measurements of the acid-denatured state of ACBP at pH 2.356,57 (Supplementary Figure S10). Consistent with previous NMR chemical shift3 and PRE4 studies, our simulations predict long-range contacts in the unfolded-state ensemble between residues in helix 2 and 3, and helix 2 and 4 (Figure 5d, Supplementary Figure S3). We find fewer contacts involving helix 1, supporting earlier reports that helix 1 is largely detached from the rest of the ACBP structure4, only forming experimentally detectable long-range contacts late in folding reaction3,58. Average RMSD-to-native values for individual helices over time (at 330K starting from the extended state) show helix 1 has a relaxation timescale of ~350 ns, while helices 2, 3 and 4 form compact, non-native structures by ~100 ns, with helix folding/unfolding presumably occurring on timescales slower than ~15 µs (data not shown).
Slightly more helicity (~20%) and more specific long-range contacts (mostly between residues in helix 2 and 3) are seen in the higher temperature simulations (370K, ~0.6–1.0 M GuHCl). This is likely due to the GBSA solvent model used, which does not model temperature-dependent effects, and to the increased conformational sampling at higher temperature. The exact prediction of helix content has little impact on our polymer-theory analysis, as scaling statistics are insensitive to secondary structure content59. We note, however, that overestimates of helicity could bias the folding seen in the MSM toward a ‘diffusion-collision’ mechanism.
Complexity underlies simple kinetics
The network of transition rates in an MSM model specifies a continuous-time chemical master equation whose solution yields a spectrum of implied timescales, each corresponding to a relaxation mode describing population flux on that timescale36,37,43. This spectrum is broad and continuous, reflecting the large number of dynamic transitions between competing metastable states occurring on many timescales (Supplementary Figure S5). This kinetic detail may be difficult to fully resolve experimentally, as structural observables typically report ensemble-averaged quantities, sensitive to specific kinds of structural transitions (e.g. FRET is most sensitive to changes in interatomic distances near the Förster radius.)
Which relaxation modes of ACBP are most sensitively reported by FRET probes? To predict the relaxation timescales observable by the ACBP 17–88 FRET probe, we projected the MSM population dynamics onto a proxy observable, the distance between residues 17 and 86, which can be more easily computed from simulations (since our simulations do not include C-terminal Gly-Cys residues 87 and 88). The predicted (ensemble-average) time course of this proxy distance is a superposition of relaxation modes of different amplitudes (Figure 7a, see Methods). Interestingly, the model shows only two timescale regimes* expected to exhibit a large signal. A prudent experimentalist would fit such observed traces to a bi-exponential curve, postulating a three-state model, even though the underlying dynamics are considerably more complex.

Figure 7
The FRET distance observable is sensitive to two main relaxation timescales. The continuous-time dynamics of the MSM state populations was calculated via the chemical master equation (see Methods). Observable values over time were computed as the sum of projections to the 1000 slowest relaxation modes. Shown in
(a) are the MSM dynamics, starting from initial unfolded populations, projected onto the distance between 17 and 86 (blue, thick), with traces of individual modes shown below this. (Since our simulations do not include the C-terminal Gly-Cys residues, 17–86 is used as a proxy for the FRET distance observable 17–88.)
(b) The amplitudes of each mode, plotted versus each implied timescale, reveal that, despite a broad distribution of kinetic timescales in the model, only two regimes contribute appreciably to the observed signal: ~0.1–3 ms (folding) and ~10 µs (unfolded-state structuring). Note that these timescales are slightly faster than experiment due to forcefield and rate estimation effects.
(c) The calculated rate spectrum for the projection in (a) shows these two regimes clearly.
(d) Rate spectra calculated from experimental FRET mixer traces for W55F, F26A and Y31N (data from Figure 2a) show relaxations corresponding to unfolded-state structuring on the ~100 µs timescale (colored lines and shaded rectangles are timescales calculated from single-exponential fits to the data, and their uncertainties). The ~9 ms folding timescale (black dashed line) is not accessible in the FRET mixer experiments, so peaks corresponding to the global folding rate are absent.
The relaxation modes with significant amplitudes cluster around two important timescale regimes: ~0.1–3.0 ms, corresponding to the overall folding relaxation, and timescales near ~1–10 µs, corresponding to structuring in the unfolded state (Figure 7b). We note that these predicted timescales are faster than experiment by an order of magnitude, with a broad spread in the slowest (folding) relaxation timescales, both of which are likely due to forcefield and transition rate estimation effects. The resolution of the MSM can be improved in the future with additional sampling.
To better compare these predictions to experimental FRET traces, a new method is used to calculate spectra of relaxation timescales from time series data60,61. These so-called rate spectra are obtained by finding a spectrum of rate amplitudes ai such that Σi ai exp(−t/τi) best fits an observed time course for a set of timescales τi. The spectra thus obtained are “dynamical fingerprints”62 of the observed kinetics, and can be thought of as a numerical inverse Laplace transform, in which regularization methods are used to avoid overfitting to noise.
The rate spectra of both simulation data (Figure 7c) and mixer traces (Figure 7d) reveal similar kinetic phases. Rate spectra calculated from experimental FRET mixer traces for W55F, F26A and Y31N (data from Figure 2a) show relaxations corresponding to unfolded-state structuring on the ~100 µs timescale. While experimental limitations (e.g. signal-to-noise) limit the resolution of the rate spectra, a strong qualitative connection between the complex behavior seen in simulation to experiment, as well as quantitative agreement of the location of the peaks in the experimental rate spectra. In most cases, the relaxation timescales obtained from exponential curve fits match the peaks in the rate spectra, although the rate spectra approach is more robust and less sensitive to noise (Supplementary Figure S11, see SI section A.4).
The presence of a very small peak at ~3 ms in the rate spectrum of the simulated time course, near the slowest implied timescale of the MSM. The existence of this separate peak is likely an artifact due to the broad spread of relaxation timescales (~0.1–3 ms), and should be attributed to the folding transition. Inspection of the transition matrix eigenvectors corresponding to each implied timescale show similar structural events for all of these relaxation modes: ensembles of compact unfolded conformations transitioning to the native state (Supplementary Figure S12).
Discussion
Complex, multi-state kinetics is a general phenomenon in biopolymer folding studies, and find it plausible that a great deal of complexity in protein folding is commonly masked in a macroscopic interpretation of ensemble, and even single-molecule experiments62. It is very noteworthy that several new single-molecule studies of protein folding have found conformational fluctuations indicating multiple distinct metastable states63,64. Even the most sophisticated single-molecule experiments, however, cannot resolve the entire microscopic complexity of folding due to the limited number of photons that can be detected on the microsecond timescale. It is therefore likely that ensemble and single molecule fast kinetic observables cannot capture the full complexity of folding, and instead we must turn to computer simulation. Markov State Model approaches is expected to be increasingly useful in this regard, as direct comparisons to experiment can made by projecting predicted microscopic dynamics onto macroscopic observables.
The combined experimental results and MSM of the ACBP folding reaction suggest that residual unfolded-state structure forms on the ~100 µs timescale, in the absence of a well-defined intermediate.
This timescale agrees well with the rates previously reported by Teilum et al. using Trp-Dansyl FRET and a continuous flow mixer7, and the same molecular process is observed in the two studies.
Even in that study, the putative intermediate was described as being mostly unstructured, with only a ~30% increase in buried of surface area compared to the unfolded state, and with the fast ~80 µs kinetic phase insensitive to denaturant concentration.
Intriguingly, our results suggest that the slow formation of unfolded-state structure is not due to barrier-limited formation of a folding intermediate, but rather due to slow unfolded-state structuring, possibly through a continuum of states. Strong agreement is find between the mean-FRET efficiency of the denatured subpopulation at equilibrium and the asymptotic mean-FRET efficiency of the slow, kinetically resolvable phase in the nonequilibrium mixing experiment. In our mixing experiments (from 6 M to 0 M GuHCl), the measured FRET reaches ~90% of the native-state FRET over the course of ~200 µs. This implies that any intermediate I must have native-like FRET (as characterized previously7), and that the unfolded U state must have low FRET and be highly populated at high denaturant concentrations. But if the time-resolved FRET, is indeed due to the relatively slow (~100 µs) interconversion of discrete low-FRET and high-FRET states, significant line-broadening of the denatured subpopulation in the sm-FRET experiments is seen. Such line broadening has been shown by Rieger et al.47 using smFRET with ALEX and a similar confocal transit time to detect an unfolded intermediate of RNase H at ~ 0.7 FRET, differentiated from the native state (0.8 – 1.0 FRET).
A signature of such an intermediate is a very broad unfolded-state FRET histogram that results from averaging and shot noise.
In contrast, the unfolded-state FRET histograms are narrow, comparable with Protein L, which does not populate a folding intermediate.
Although the possibility cannot rule out that U and I substates are obscured by shot noise or fast averaging, and note that we can only make relative comparisons of single-molecule and time-resolved FRET, believing the weight of the evidence argues against the barrier-limited formation of an intermediate.
Instead, the changes in FRET over time observed in the mixer must correspond very closely to the unfolded-state compaction seen in decreasing concentrations of denaturant by smFRET.
Early events in the folding reaction are predicted by the MSM to be structurally heterogeneous, suggesting collapse-like behavior with a gradual acquisition of non-local residual structure.
Non-specific hydrophobic collapse has been characterized as occurring on the ~100 ns timescale65, so slow collapse in ACBP is surprising, although other studies have characterized non-specific collapse forming on timescales less than 150 µs66–68. Consistent with this picture is slow dynamics in protein unfolded states characterized here and elsewhere49, as well as slow dynamics predicted by the MSM.
The Bayesian estimates of average Arrhenius folding barriers separating MSM metastable states38 are small— ~1.64 ± 1.04 kcal/mol for the 20k-microstate model (Supplementary Figure S13)—but the overall hub-like connectivity structure of the network can contribute to slow kinetics.
It is interesting to compare the predictions of unfolded structure with the results of a recent simulation study by Shaw et al. of the acid-denatured unfolded state of ACBP, in which a single 200 µs-trajectory was simulated 47. Tens are obtained of thousands of independent trajectories amounting to tens of milliseconds of aggregate simulation time.
Not surprisingly, even though both simulations predict long-range structure between helices 2 and 4, a great deal more heterogeneity in long-range contacts, reflecting both native and non-native interactions between residues normally participating in the hydrophobic core of ACBP.
The relaxation timescales observed for individual helices is consistent with the faster folding/unfolding timescales of helix 1 observed by Shaw et al.
Conclusion
MSM model of ACBP folding is constructed that reveals a complex network of metastable states with slow dynamics in the unfolded ensemble due to non-random residual structure and heterogeneous folding pathways. Validation of this model using smFRET, intramolecular diffusion and fast microfluidic mixing experiments suggests that the folding reaction for ACBP involves a surprisingly slow acquisition of unfolded-state structure in helix 2, 3 and 4 on the ~100 µs timescale, followed by barrier-limited folding to the native state on the ~10 millisecond timescale.
Moreover, the combined simulation and experimental studies of ACBP show how the microscopic complexity of folding can be reconciled with the simple macroscopic behavior often seen in bulk experiments.
Despite its inherent microscopic complexity, the MSM model of ACBP predicts that experimental observables probing intramolecular distance should exhibit simple bi-exponential kinetics.
In many other molecular systems—vesicle fusion, polymer dynamics, small molecule conformers, etc.—complex dynamics may also underlie simpler experimental observations.
MSM approaches like those described here may provide a general framework for taming these processes and explaining how their simple macroscopic behavior arises.
ABBREVIATIONS
ACBP : acyl-coenzyme A-binding protein
FRET : Förster resonance energy transfer
smFRET : single-molecule FRET
GuHCl : guanidinium hydrochloride
PR : proximity ratio
MSM : Markov State Model
GPU : graphics processing unit
GBSA : generalized Born-surface area
MBAR : multi-state Bennett acceptance ratio
NTL9 : N-terminal domain of ribosomal protein L9
RMSD : root-mean-squared deviation
PRE : paramagnetic relaxation enhancement
https://www.nature.com/articles/s41467-020-19023-1
FRET experiments can provide state-specific structural information of complex dynamic biomolecular assemblies.
However, to overcome the sparsity of FRET experiments, they need to be combined with computer simulations.
A program suite is introduice with (i) an automated design tool for FRET experiments, which determines how many and which FRET pairs should be used to minimize the uncertainty and maximize the accuracy of an integrative structure, (ii) an efficient approach for FRET-assisted coarse-grained structural modeling, and all-atom molecular dynamics simulations-based refinement, and (iii) a quantitative quality estimate for judging the accuracy of FRET-derived structures as opposed to precision.
Tools are benchmarked against simulated and experimental data of proteins with multiple conformational states and demonstrate an accuracy of ~3 Å RMSDCα against X-ray structures for sets of 15 to 23 FRET pairs.
Free and open-source software for the introduced workflow is available at https://github.com/Fluorescence-Tools.
- LabelLib : Library for coarse-grained simulations of probes flexibly coupled to biomolecules. pymol, fluorescence, simulation-toolkit, fret.
- Olga : FRET-screening of conformations and experiment planning. fluorescence, molecules, fret, conformations. C++
- FRETrest : Helper scripts for FRET-restrained MD simulations. Generate AMBER restraint files (DISANG). Python
- FRETlines : Jupyter Notebook
- QuEst - Quenching Estimator for fluorophores coupled to proteins. simulation, fluorescence, fret, quenching, dyes, Jupyter Notebook
Estimateur d'extinction pour les fluorophores couplés aux protéines
- Chisurf : Global analysis platform for fluorescence data. correlation, protein, fluorescence, spectroscopy, multiple-datasets, fluorescence-data,global-analysis, Python
- mdtraj_fps ia a command line tool to calculate FRET observables form MD-trajectories. single-molecule, fluorescence, spectroscopy, Python
Automated and optimally FRET-assisted structural modeling : https://www.nature.com/articles/s41467-020-19023-1
A web server for FRET-assisted structural modeling of proteins
The NMSim Web Interface http://www.nmsim.de Heinrich-Heine-Universität Düsseldorf
NMSim is a normal mode-based geometric simulation approach for exploring biologically relevant conformational transitions in proteins.
The approach has been shown to reproduce experimentally observed conformational variabilities in the case of domain and loop motions and is able to generate meaningful pathways of conformational transitions.
The generated structures are of good stereochemical quality.
Thus, they can serve as input to docking approaches or as starting points for more sophisticated sampling techniques.

The PDB file must not be larger than 5000 atoms.
Structural preparation before simulation:
- Incomplete residues will be fixed.
- Waters and ligands will be removed.
- Hydrogens will be added (are not required for input PDB file).
PDB ID Type of simulation:
- Small scale motions
(loops, docking ensembles, distinct starting structures)
- Large scale motions
(opening and closing of domains)
- Radius of gyration-guided motions
(biased simulation towards lower (or larger) ROG)
Targeted simulation : Target PDB-File
Rigid cluster decomposition parameters (FIRST):
- E-cutoff for H-bonds
- Hydrophobic method
- Hydrophobic cutoff
Normal mode parameters (RCNMA): RCNMA, ENM, Cutoff for C-alpha atoms
Simulation parameters (NMSim):
- No. of trajectories
- No. of NMSim cycles
- Side-chain distortions
- Step size
- No. of sim. cycles
- Output frequency
- NM mode range
- ROG mode
https://pubs.acs.org/doi/10.1021/acs.jpcb.8b10005
Unbiased Atomistic Insight into the Mechanisms and Solvent Role for Globular Protein Dimer Dissociation
Chercher et Trouver c'est Jouer et Gagner
L'arrivée du Web et d'Internet a permis de publier inviduellement et en groupe plus rapidement voire même en temps réel, en créant des liens virtuels et en hypertextes à partir ou vers quoi la pensée se pose, réfléchit et évolue selon des références officielles ou "bien pensantes" des gens de pouvoir, pour faire valoir ou se faire valoir, et/ou de la même façon avec des références plus contradictoires menant à la discution plus ou moins profonde et argumentée dans un soucis de s'exprimer et de convraincre soi-même et les autres de ses propre pensées, et de leur fonctionnement dans les systèmes multimédias pour engendrer l'action voire la création.
L'arrivée de Jeu numérique a permis d'utiliser les théories des jeux en général, en stratégies optimisées, pour répondre à des objectifs, des volontés et désirs, et de les intégrer comme projectif à la représentation des concepts sujet-objet-projet, avec l'extansion aux scénario (personnage synthétiques simulant un comportement, une vie propre individuelle), aux mises en scènes (intégrant les acteurs synthétiques dans des environnements actifs et cadre de vie dynamiques, voire mixtes en Réalité Augmentée) et aux mises en jeux avec des gains et/ou des pertes selon des contraintes, des encadrements, des degrés de liberté dans des systèmes de régulation ou de simulation testant les excès en valeur et comportements excessifs, disruptifs ou distorsifs (ou pas, et autres).
Foldit (littéralement « Pliez-la », sous entendant pliez la protéine) est un jeu vidéo expérimental sur le repliement des protéines,
développé en collaboration entre le département d'informatique et de biochimie de l'université de Washington.
La version bêta a été publiée en mai 2008. Les joueurs tentent de résoudre un problème que les ordinateurs ne savent pas résoudre.
Version humaine de Rosetta@home et développée par la même équipe, Foldit utilise les algorithmes de ce dernier, notamment pour le calcul d'énergie des protéines.
De nombreux puzzles proposés aux joueurs de Foldit sont d'ailleurs issus de prévisions calculées par Rosetta.
Un autre exemple de jeu comme celui-ci est le jeu ESP (en) (alias le Google Image Labeler).
Le processus par lequel les êtres vivants créent la structure primaire des protéines, la biosynthèse des protéines, est assez bien compris.
Cependant, déterminer comment la structure primaire d'une protéine se transforme en une structure tridimensionnelle, c'est-à-dire comment la molécule se « plie », est plus difficile.
Le processus général est connu, mais la prédiction des structures protéiques est un calcul compliqué.
Foldit tente d'utiliser les capacités naturelles du cerveau humain pour résoudre ces problèmes (logique, déduction, raisonnement).
Les puzzles actuels sont basés sur des protéines qui sont déjà comprises ;
et c'est en analysant la façon dont les humains abordent ces puzzles que les chercheurs espèrent améliorer les algorithmes employés par les logiciels de pliage des protéines.
Foldit fournit une série de tutoriels dans lesquels l'utilisateur manipule des structures de protéines.
L'application affiche une représentation graphique de la structure de la protéine, et l'utilisateur peut alors la manipuler à l'aide d'un ensemble d'outils.
Lorsque la structure est modifiée, un « score » correspondant au niveau d'énergie de la protéine est calculé en fonction de la façon dont elle est pliée.
Une liste des meilleurs scores pour chaque puzzle est enregistrée.
Les joueurs peuvent automatiser certaines tâches à l'aide de scripts surnommés « recettes ».
Ces scripts, écrits en Lua ont fait l'objet d'une publication de l'équipe de Foldit dans le journal PNAS, certains des algorithmes proposés par ces recettes atteignant des efficacités proches des algorithmes professionnels 1.
Bloqués depuis plus de 10 ans par la complexité de la protéase rétrovirale du virus M-PMV (Mason-Pfizer monkey virus), les chercheurs n'arrivaient pas à trouver sa structure tridimensionnelle.
Cette structure est essentielle pour identifier des sites potentiels que pourraient cibler des protéines-médicament.
Ils ont alors décidé de passer par Foldit et au bout de 3 semaines seulement, la revue Nature Structural & Molecular Biology publie la structure 3D de l'enzyme,
citant au passage les « joueurs » ayant participé à sa découverte comme coauteurs.
Maintenant les biologistes peuvent commencer à chercher des molécules (protéines) capables d'inhiber cette protéase.
Si une telle molécule est trouvée, la reproduction du VIH serait empêchée et l'infection stoppée2.
Genes splicing (épissage des ARN)
https://fr.wikipedia.org/wiki/%C3%89pissage
Chez les eucaryotes (organismes à noyau), l’épissage est un processus par lequel les ARN transcrits à partir de l'ADN génomique peuvent subir des étapes de coupure et ligature qui conduisent à l'élimination de certaines régions dans l’ARN final.
Les segments conservés s’appellent des exons et ceux qui sont éliminés s’appellent des introns.
Chez les eucaryotes (organismes à noyau), l’épissage est un processus par lequel les ARN transcrits à partir de l'ADN génomique peuvent subir des étapes de coupure et ligature qui conduisent à l'élimination de certaines régions dans l’ARN final.
Les segments conservés s’appellent des exons et ceux qui sont éliminés s’appellent des introns.

Lors de la transcription de gènes codant des protéines, un ARN pré-messager est synthétisé puis est épissé dans le noyau de la cellule pour donner lieu à l’ARN messager dit mature.
L’ARNm mature, constitué des seuls exons, est alors exporté vers le cytoplasme pour être traduit en protéine. Les mécanismes de contrôle s'assurent que les ARNm ont été correctement épissés avant de permettre leur exportation.
L’épissage est catalysé par un ensemble de complexes ribonucléoprotéiques appelé collectivement spliceosome (épissage se disant splicing en anglais).
Chaque complexe, appelé petite ribonucléoprotéine nucléaire, contient un ARN et plusieurs protéines.
L'épissage des ARNm est également catalysé par les snARN (small nuclear ARN) qui sont de petits ARN non codants liés à des protéines.
Il existe également des introns appelés auto-épissables ou auto-catalytiques, c’est-à-dire capables de s’exciser sans intervention d’un spliceosome, dans les mitochondries, les plastes et certaines bactéries.
Cependant, au moins dans les mitochondries et les chloroplastes, certains de ces introns nécessitent l’intervention de protéines nucléaires.
Le mécanisme catalytique du spliceosome est encore imparfaitement connu, mais par analogie avec le fonctionnement du ribosome, on pense que c'est l’ARN qui est catalytique,
et donc que le spliceosome est un ribozyme, c'est à dire ARN qui possède la propriété de catalyser une réaction chimique spécifique.
Le terme « ribozyme » est un mot-valise formé à partir des mots « acide ribonucléique » et « enzyme ».
L'épissage est beaucoup plus long que la transcription, cette dernière durant quelques minutes contre environ une heure et demie pour l'épissage.
L'épissage (en anglais splicing) est un mécanisme de maturation de l'ARN qui permet à un ARN transcrit à partir d'un gène (ARN pré-messager), de se débarrasser de séquences non-codantes (les introns),
pour donner un ARN messager, ou ARNm, qui sera ensuite traduit en protéine dans le cytoplasme de la cellule.
Comme les gènes sont composés d'introns et d'exons, on dit qu'ils sont morcelés.
Les exons sont généralement de courtes séquences, tandis que les introns sont bien plus longs.
Les ARNt (ARN de transfert) et ARNr (ARN ribosomique) subissent aussi un épissage.
Des enzymes interviennent sur l'ARN pré-messager qui est la copie de l'ADN du gène ; par exemple, les ribozymes catalysent des réactions de l'épissage.
Des séquences présentes sur l'ARN pré-messager servent de signaux d'épissage, de part et d'autre des introns.
Des ribonucléoprotéines nucléaires (snRNP) interviennent dans l'épissage : ces molécules sont formées de protéines et de molécules d'ARN.
Ces molécules travaillent au sein du complexe d'épissage ou splicéosome, un ensemble plus vaste de molécules d'ARN et de protéines, qui coupe et recolle l'ARN.
Les cellules « eucaryotes » (entre 10 µm et 33 m de long, apparu à plus de 1,6 à 2,6 milliards d'années) possèdent un noyau et des organites (réticulum endoplasmique, appareil de Golgi, plastes divers, mitochondries, etc.) délimités par des membranes.
Les eucaryotes se distinguent des procaryotes (comme les bactéries) qui sont pour leur part dépourvus de ces structures.
Il existe également une autre différence significative entre procaryote et eucaryote : la structure des brins d’ADN. Chez les eucaryotes, le matériel génétique est enfermé dans le noyau sous la forme de plusieurs brins linéaires qui se condensent lors des divisions cellulaires, les chromosomes. Les bactéries disposent quant à elles d'un seul chromosome circulaire. Il forme donc une boucle.
À partir d'un même ARN pré-messager, il est possible d'obtenir différents ARNm, selon les séquences conservées ou supprimées dans la version finale.
Un même ARN pré-messager peut donc conduire à la production de différentes protéines.
La plupart de nos gènes feraient l'objet d'un épissage alternatif.
Par conséquent, s'il existe 30.000 à 40.000 gènes fonctionnels chez l'Homme, le nombre de protéines produites est plus élevé.
Des anomalies dans l'épissage alternatif des gènes peuvent être impliquées dans des cancers.
C'est pourquoi certaines thérapies ciblent l'épissage alternatif.
Des mutations conduisant à des épissages aberrants peuvent conduire à des maladies génétiques.
L'épissage alternatif concerne aussi les virus, comme le virus de l'hépatite B ou le VIH.
pour donner un ARN messager, ou ARNm, qui sera ensuite traduit en protéine dans le cytoplasme de la cellule.
Comme les gènes sont composés d'introns et d'exons, on dit qu'ils sont morcelés.
Les exons sont généralement de courtes séquences, tandis que les introns sont bien plus longs.
Les ARNt (ARN de transfert) et ARNr (ARN ribosomique) subissent aussi un épissage.
Des enzymes interviennent sur l'ARN pré-messager qui est la copie de l'ADN du gène ; par exemple, les ribozymes catalysent des réactions de l'épissage.
Des séquences présentes sur l'ARN pré-messager servent de signaux d'épissage, de part et d'autre des introns.
Des ribonucléoprotéines nucléaires (snRNP) interviennent dans l'épissage : ces molécules sont formées de protéines et de molécules d'ARN.
Ces molécules travaillent au sein du complexe d'épissage ou splicéosome, un ensemble plus vaste de molécules d'ARN et de protéines, qui coupe et recolle l'ARN.
Les cellules « eucaryotes » (entre 10 µm et 33 m de long, apparu à plus de 1,6 à 2,6 milliards d'années) possèdent un noyau et des organites (réticulum endoplasmique, appareil de Golgi, plastes divers, mitochondries, etc.) délimités par des membranes.
Les eucaryotes se distinguent des procaryotes (comme les bactéries) qui sont pour leur part dépourvus de ces structures.
Il existe également une autre différence significative entre procaryote et eucaryote : la structure des brins d’ADN. Chez les eucaryotes, le matériel génétique est enfermé dans le noyau sous la forme de plusieurs brins linéaires qui se condensent lors des divisions cellulaires, les chromosomes. Les bactéries disposent quant à elles d'un seul chromosome circulaire. Il forme donc une boucle.
L’épissage alternatif
À partir d'un même ARN pré-messager, il est possible d'obtenir différents ARNm, selon les séquences conservées ou supprimées dans la version finale.
Un même ARN pré-messager peut donc conduire à la production de différentes protéines.
La plupart de nos gènes feraient l'objet d'un épissage alternatif.
Par conséquent, s'il existe 30.000 à 40.000 gènes fonctionnels chez l'Homme, le nombre de protéines produites est plus élevé.
Des anomalies dans l'épissage alternatif des gènes peuvent être impliquées dans des cancers.
C'est pourquoi certaines thérapies ciblent l'épissage alternatif.
Des mutations conduisant à des épissages aberrants peuvent conduire à des maladies génétiques.
L'épissage alternatif concerne aussi les virus, comme le virus de l'hépatite B ou le VIH.
https://endpoints.elysiumhealth.com/three-scientists-who-changed-our-understanding-of-dna-6833c1a057a0
(Elysium Health, Apr 16, 2018).
When scientists from Cambridge University and King’s College London uncovered the structure of DNA six decades ago, they cracked the genetic code and how it’s replicated from one cell to the next, and one generation to the next.
The discovery gave scientists an unprecedented way of studying the root causes of inherited diseases and a potential pathway to cures. It shed light on the aging process, gave way to early sequencing techniques, and eventually set in motion one of the most important scientific projects in history: the Human Genome Project. Today, for the first time ever, we are at a place where scientists can precisely analyze, add to, subtract from, and alter the code of life of every living creature on Earth..
The scientists profiled by the team at Elysium Health, giants in their respective fields, are continuing to tell the story of DNA, fulfilling the promise of genetic sequencing and engineering to solve quandaries in aging and disease, and at the same time, further illuminating what it means to be human.
As part of his dissertation at Harvard in 1984, George Church (Geneticist) developed a direct genome sequencing technique, which contributed to the Human Genome Project (HGP).
Now a professor of genetics at Harvard Medical School and founding core faculty and lead for synthetic biology at the Wyss Institute, Church’s innovations have contributed to nearly all “next generation” DNA sequencing methods and companies.
Church currently directs the Personal Genome Project (PGP), a long-term cohort study that allows scientists to connect human genetic information (human DNA sequence, gene expression, associated microbial sequence data, and more) with human trait information (medical information, biospecimens, and physical traits) and environmental exposures.
“This is still really what my group is focused on, trying to understand what enzymes have improved DNA repair activity in long-lived species, and how that works,” says Gorbunova (Biologist). “Because if we can understand that, maybe we can enhance it.”
While conducting research at Cold Spring Harbor Laboratory in the 1970s, Richard Roberts, Molecular Biologist, discovered RNA splicing, which led to his Nobel Prize in 1993.
When a sequence of DNA is copied it becomes RNA, and RNA contains instructions for making proteins.
During RNA splicing, non-coding regions, called introns, are cut out, and the remaining coding segments, exons, are pasted together to form a mature messenger RNA (mRNA).
Since errors in RNA splicing can result in mutations, scientists use RNA splicing to better understand the underlying mechanisms that cause genetic diseases.
RNA splicing errors account for up to 15 percent of human diseases, ranging from neurological to metabolic disorders.
“This research area is so fundamental that if you want to work on anything that is involved in humans, whether it’s good stuff or bad stuff, whether it’s disease or otherwise, you have to know the structure of the genes, how they’re laid out, how they’re processed, and what goes on. This is just one step along the way.”
These days, Roberts is interested in understanding the biological effects of DNA methylation, a mechanism cells use to control gene expression.
Before CRISPR, Roberts isolated most of the world’s first “molecular scissors.” His groundbreaking work at Jim Watson’s lab, are the similarities between gene splicing and making a movie, and why genetically modified foods aren’t bad.
Gene splicing: The chemical process, involving restriction enzymes, of cutting out part of a DNA in a gene and adding new DNA in its place.
Travaux en cours
GBM-LAB avec le BOINC.BERKELEY.EDU
https://boinc.berkeley.edu/GBM-LAB avec le BOINC.BERKELEY.EDU
BOINC lets you help cutting-edge science research using your computer.
The BOINC app, running on your computer, downloads scientific computing jobs and runs them invisibly in the background. It's easy and safe.
About 30 science projects use BOINC. They investigate diseases, study climate change, discover pulsars, and do many other types of scientific research.
The BOINC and Science United projects are located at the University of California, Berkeley and are supported by the National Science Foundation.


GPUGRID.net is a distributed computing infrastructure devoted to biomedical research.
RNA World (beta) is a distributed supercomputer that uses Internet-connected computers to advance RNA-related research.
World Community Grid
Scientists at Scripps Research are doing
molecular modeling simulations to look for possible candidates for the
development of treatments for COVID-19, but to be successful they need
massive computing power to carry out millions of simulated laboratory
experiments.
So Scripps Research is partnering with World Community Grid, an IBM social impact initiative that allows anyone with a computer and an internet connection to donate their device’s computing power to help scientists study the world’s biggest problems in health and sustainability.
By using this donated computing power, the scientists aim to identify promising chemical compounds for further laboratory testing.
The research team wants not only to help find treatments for COVID-19, but also to create a fast-response, open source toolkit that will help all scientists quickly search for treatments for future pandemics.
And in keeping with World Community Grid's open data policy, all data and tools that are developed through this project will be shared freely in the scientific community.
The project’s primary goal is to search for potential treatments for COVID-19, so studying proteins from SARS-CoV2 (the virus that causes COVID-19) is the highest priority.
Additionally, scientists want to fight not only the current emergency, but also prepare for the ones that will likely follow.
Future pandemics could stem from a progressive accumulation of mutations, which can eventually lead to a new virus variant.
This is what happened when the virus SARS-CoV1 mutated to become SARS-CoV2.
So, the research team is including proteins from the SARS-CoV1 and other viruses to be studied as part of OpenPandemics –COVID-19, which will help them assess how difficult would it be to find or design molecules capable of overcoming the inevitable mutations.
So Scripps Research is partnering with World Community Grid, an IBM social impact initiative that allows anyone with a computer and an internet connection to donate their device’s computing power to help scientists study the world’s biggest problems in health and sustainability.
By using this donated computing power, the scientists aim to identify promising chemical compounds for further laboratory testing.
The research team wants not only to help find treatments for COVID-19, but also to create a fast-response, open source toolkit that will help all scientists quickly search for treatments for future pandemics.
And in keeping with World Community Grid's open data policy, all data and tools that are developed through this project will be shared freely in the scientific community.
The project’s primary goal is to search for potential treatments for COVID-19, so studying proteins from SARS-CoV2 (the virus that causes COVID-19) is the highest priority.
Additionally, scientists want to fight not only the current emergency, but also prepare for the ones that will likely follow.
Future pandemics could stem from a progressive accumulation of mutations, which can eventually lead to a new virus variant.
This is what happened when the virus SARS-CoV1 mutated to become SARS-CoV2.
So, the research team is including proteins from the SARS-CoV1 and other viruses to be studied as part of OpenPandemics –COVID-19, which will help them assess how difficult would it be to find or design molecules capable of overcoming the inevitable mutations.
https://boinc.bakerlab.org/rosetta/
Determine the 3-dimensional shapes of proteins in research that may ultimately lead to finding cures for some major human diseases. By running Rosetta@home you will help us speed up and extend our research in ways we couldn't possibly attempt without your help. You will also be helping our efforts at designing new proteins to fight diseases such as COVID-19, HIV, malaria, cancer, and Alzheimer's
ACEMD Platform is a complete and fast solution package, designed to run and analyze your molecular dynamics (MD) simulations. It includes ACEMD, Parameterize and HTMD packages. ACEMD is the MD engine that runs the simulation, Parameterize is a force field parameterization tool for small molecules and HTMD is a Python package that you can use to create systems, prepare them and, once ACEMD has finished simulating those systems, analyze their trajectories.
Rosetta et le FOLDING sont deux approches différentes, BOINC est une plate-forme ouverte pour la recherche qui permet à de nombreux projets académiques de coexister et puisque le FOLDING n'est pas un projet BOINC, le choix est assez simple au niveau du processeur. GPUGRID est le plus proche de Folding que vous obtiendrez sur la plate-forme BOINC et il fonctionne sur des unités de traitement graphiques au lieu de CPU.
Les protéines sont les éléments constitutifs de notre corps humain et elles sont elles-mêmes constituées de plus petites pièces appelées acides aminés.
Les protéines sont une extraordinaire pièce complexe de machinerie biologique, capable de s'auto-assembler et de transformations et adaptations continues qui sont causées par ce qui se passe autour d'elles.
Elles peuvent changer de forme en fonction de la température, des éléments chimiques présents autour d'eux et d'autres dynamiques, mais peut-être le fait le plus remarquable est que les protéines sont fondamentalement capables de s'auto-assembler à partir de rien en supposant que tout autour d'elles est sans problème.

Le processus de pliage (Folding) ou comment une protéine s'assemble elle-même dans sa forme finale.
Étant
la machinerie complexe, parfois les choses peuvent mal se passer
pendant leur auto-assemblage. Un accident souvent connu sous le nom de
"mauvais pliage".
Et Folding@home se concentre sur la reproduction de toutes les étapes exactes d'un tel processus, soit une énorme quantité de fois et dans des conditions différentes afin qu'ils puissent parfois assister à un mauvais pliage et ensuite essayer de comprendre ce qui a causé un tel accident à se produire dans cette simulation particulière.
Les causes peuvent souvent être plus d'une et pour vraiment comprendre ce qui se passe, vous avez besoin d'avoir beaucoup de mauvais plis à observer et idéalement, vous voulez avoir autant d'informations que possible sur de tels événements, c'est pourquoi Folding@home simule le processus de pliage atome par atome, un effort de calcul coûteux qui est connu sous le nom de dynamique moléculaire.
Le "mauvais pliage" a un intéret particulier, car il est considéré comme la cause de plusieurs maladies importantes que nous ne pouvons pas encore guérir et qui sont également connus sous le nom de Protéopathies.
Simuler un atome de protéine par atome et voir ce qui se passe instant par instant est en soi un processus long et douloureux qui devient de plus en plus long et douloureux plus il y a d'atomes à simuler (de plus grandes protéines) et plus la durée de la simulation est longue, ce qui signifie essentiellement que beaucoup de compromis doivent être faits si vous voulez utiliser cette approche avec le niveau technologique actuel : certains de ces compromis peuvent impliquer la réalisation de simulations avec des modèles simplifiés, la simulation de très petites protéines ou de très petits délais. D'où la décomposition des molécules et l'utilisation d'un immense réseau international d'ordianteur en parallel.
Utiliser Rosetta a ses avantages, sachant que la simulation d'énormes protéines atome par atome pendant une longue période de temps est très intensive en calcul (lire : temps perdu ne faisant pas autre chose, argent dépensé pour faire tourner les ordinateurs à plein régime) et beaucoup de processus peuvent encore être reproduits avec une approximation suffisante même sans simuler atome par atome.
Rosetta ne se concentre pas sur ce qui se passe dans le design du processus, mais sur la prédiction du type de statut final (structure quaternaire) que vous obtiendriez si vous commenciez avec le statut initial (structure primaire) donnant plusieurs variables sur l'environnement.
Beaucoup d'hypothèses sont faites et beaucoup de détails approximatifs sont laissés de côté : Une tâche typique de Rosetta exécute toujours des "étapes", mais cette fois-ci, ils n'essayent pas de calculer où chaque atome sera selon les lois physiques (par lois physiques, je veux dire, entre autres choses, les forces d'attraction et de répulsion entre les atomes. C'est ce sur quoi se concentre Folding@home).
Au lieu de cela, Rosetta fait un "mouvement" quelque peu aléatoire d'un morceau entier et il va seulement à l'étape suivante quand un des mouvements aléatoires a rendu la protéine entière plus stable qu'avant ("niveau d'énergie inférieur"). Cela fonctionne parce que dans la nature tout ce qui vous entoure essaie constamment de passer à des configurations plus stables (niveaux d'énergie inférieurs).
Ce qui permet d'exécuter beaucoup plus de simulations de protéines beaucoup plus grandes et de périodes beaucoup plus longues, pour un nombre beaucoup plus grand de protéines.
Donc les deux projets ayant fait des publications scientifiques, ils ont leurs mérites et font tous deux quelque chose d'utile à l'humanité qui est d'identifier un problème et de choisir une approche pour mieux le comprendre.
Pour appliquer nos théories, les deux méthodes sont intéressantes. L'une Folding@Home pour appliquer les processus markoviens prétopologiques.
L'autre pour tester l'aléa sur la trans-combinaoire au lieu de la simple combinatoire de l'histogramme, avec une intelligence artificielle.
Et Folding@home se concentre sur la reproduction de toutes les étapes exactes d'un tel processus, soit une énorme quantité de fois et dans des conditions différentes afin qu'ils puissent parfois assister à un mauvais pliage et ensuite essayer de comprendre ce qui a causé un tel accident à se produire dans cette simulation particulière.
Les causes peuvent souvent être plus d'une et pour vraiment comprendre ce qui se passe, vous avez besoin d'avoir beaucoup de mauvais plis à observer et idéalement, vous voulez avoir autant d'informations que possible sur de tels événements, c'est pourquoi Folding@home simule le processus de pliage atome par atome, un effort de calcul coûteux qui est connu sous le nom de dynamique moléculaire.
Le "mauvais pliage" a un intéret particulier, car il est considéré comme la cause de plusieurs maladies importantes que nous ne pouvons pas encore guérir et qui sont également connus sous le nom de Protéopathies.
Simuler un atome de protéine par atome et voir ce qui se passe instant par instant est en soi un processus long et douloureux qui devient de plus en plus long et douloureux plus il y a d'atomes à simuler (de plus grandes protéines) et plus la durée de la simulation est longue, ce qui signifie essentiellement que beaucoup de compromis doivent être faits si vous voulez utiliser cette approche avec le niveau technologique actuel : certains de ces compromis peuvent impliquer la réalisation de simulations avec des modèles simplifiés, la simulation de très petites protéines ou de très petits délais. D'où la décomposition des molécules et l'utilisation d'un immense réseau international d'ordianteur en parallel.
Utiliser Rosetta a ses avantages, sachant que la simulation d'énormes protéines atome par atome pendant une longue période de temps est très intensive en calcul (lire : temps perdu ne faisant pas autre chose, argent dépensé pour faire tourner les ordinateurs à plein régime) et beaucoup de processus peuvent encore être reproduits avec une approximation suffisante même sans simuler atome par atome.
Rosetta ne se concentre pas sur ce qui se passe dans le design du processus, mais sur la prédiction du type de statut final (structure quaternaire) que vous obtiendriez si vous commenciez avec le statut initial (structure primaire) donnant plusieurs variables sur l'environnement.
Beaucoup d'hypothèses sont faites et beaucoup de détails approximatifs sont laissés de côté : Une tâche typique de Rosetta exécute toujours des "étapes", mais cette fois-ci, ils n'essayent pas de calculer où chaque atome sera selon les lois physiques (par lois physiques, je veux dire, entre autres choses, les forces d'attraction et de répulsion entre les atomes. C'est ce sur quoi se concentre Folding@home).
Au lieu de cela, Rosetta fait un "mouvement" quelque peu aléatoire d'un morceau entier et il va seulement à l'étape suivante quand un des mouvements aléatoires a rendu la protéine entière plus stable qu'avant ("niveau d'énergie inférieur"). Cela fonctionne parce que dans la nature tout ce qui vous entoure essaie constamment de passer à des configurations plus stables (niveaux d'énergie inférieurs).
Ce qui permet d'exécuter beaucoup plus de simulations de protéines beaucoup plus grandes et de périodes beaucoup plus longues, pour un nombre beaucoup plus grand de protéines.
Donc les deux projets ayant fait des publications scientifiques, ils ont leurs mérites et font tous deux quelque chose d'utile à l'humanité qui est d'identifier un problème et de choisir une approche pour mieux le comprendre.
Pour appliquer nos théories, les deux méthodes sont intéressantes. L'une Folding@Home pour appliquer les processus markoviens prétopologiques.
L'autre pour tester l'aléa sur la trans-combinaoire au lieu de la simple combinatoire de l'histogramme, avec une intelligence artificielle.
The Institute for Protein Design
The Institute for Protein Design is located in the Molecular Engineering & Sciences / Nanoengineering & Sciences Building (map) and the J-wing of the Health Sciences Building (map) on the University of Washington Seattle campus.
https://www.ipd.uw.edu/
Designing a new world of proteins to address 21st century challenges in medicine, energy, and technology
https://www.ipd.uw.edu/coronavirus/
The World Health Organization has declared the ongoing COVID-19 outbreak, caused by the virus SARS-CoV-2, a global pandemic. The IPD is focused on seven research projects that we hope will have an immediate impact:
Antiviral and anti-inflammatory proteins : Hyperstable binding proteins are being designed to target the SARS-CoV-2 spike glycoprotein, the human ACE-2 receptor, and receptors implicated in cytokine storms.
(https://www.ipd.uw.edu/wp-content/uploads/2020/09/Cao_COVID_minibindersscience.abd9909.full_.pdf)
Protease inhibitors : A new generation of protease inhibitors made from structured macrocycles with non-canonical residues are being designed to stop SARS-CoV-2 proteases.
Screening existing drugs : Over 8,000 FDA-approved compounds are being screened in silico for binding to structures from the SARS-CoV-2 proteome.
Modeling the viral proteome : Rosetta is being used to model the 3D structures of important proteins from the SARS-CoV-2 coronavirus. (http://new.robetta.org/results.php?id=15652)
Nanoparticle vaccines : Using technology created at the IPD, an array of candidate COVID-19 vaccines has been designed, characterized, and fast-tracked into animal testing.
Serological diagnostics : LOCKR technology is being reconfigured into a sensitive in-solution serological assay to rapidly detect SARS-CoV-2 antibodies in body fluid samples.
Nanoparticles to treat inflammation : New methods for controlling cell signaling are being applied to create new nanoparticle super-agonists for regenerative medicine.
https://www.ipd.uw.edu/research/basic-areas/
Les protéines répondent déjà à une vaste gamme de défis techniques : dans la nature, elles arbitrent l'utilisation de l'énergie solaire pour fabriquer des molécules complexes, répondent à de petites molécules et à la lumière, convertissent des gradients chimiques en liaisons chimiques et transforment l'énergie chimique en travail — pour n'en citer que quelques-unes.

Le monde est au bord d'une révolution dans la conception des protéines.
De nouveaux médicaments et matériaux seront programmés sur ordinateur et produits à l'intérieur de cellules vivantes, tirant parti de la pleine échelle et de la durabilité de la biologie.
L'Institute for Protein Design a été un pionnier de longue date dans la conception de protéines computationnelles. Maintenant, grâce à un solide plan directeur et à l'appui du Projet Audacieux, la DPI s'aventurera à accélérer le rythme de la découverte, à diffuser de nouvelles technologies protéiques et à changer fondamentalement la façon dont les médicaments, les vaccins, les carburants et les nouveaux matériaux sont fabriqués.
Les cinq grands défis de l'IPD sont :





Partant de la problématique :
Les protéines sont des machines moléculaires qui font que tous les êtres vivants vivent leur vie. Elles arrêtent les infections mortelles, guérissent les cellules, captent l'énergie du soleil et bien plus encore.
Les protéines sont construites en liant des blocs chimiques appelés acides aminés, selon les instructions du génome d’un organisme.
Ces cordes "se replient" ensuite, en se basant sur les forces chimiques entre les acides aminés, formant les structures tridimensionnelles complexes nécessaires pour effectuer des tâches spécifiques.
Bien que la nature ait construit des protéines depuis plus de trois milliards d'années, le nombre de protéines possibles est astronomique : il y a plus de façons d'assembler 100 acides aminés qu'il n'y a d'atomes dans l'univers.
Les scientifiques essaient de prédire les formes que les molécules de protéines devraient prendre en fonction de leurs acides aminés — avec un succès limité.
C'est ce qu'on appelle le "problème du pliage des protéines, ou FOLDING
En raison de sa nature insaisissable, comprendre comment exploiter le pouvoir des protéines pour résoudre des problèmes est un problème en soi.
Au cours des 20 dernières années, l’équipe de recherche de David Baker a étudié les règles du pliage des protéines et les a codées dans Rosetta, une simulation informatique
qui a permis de percer dans la compréhension de la façon dont les protéines forment leur structure.
La convergence technologique de Rosetta, à l'essor de l'informatique bon marché et à la révolution génomique dans la lecture et l'écriture de l'ADN,
les chercheurs de l'Institute for Protein Design (IPD) de l'Université de Washington School of Medicine veulent concevoir de nouvelles protéines à partir de zéro avec des fonctions jamais vues dans la nature. Et grace à l'investissement du projet Audacious, l'IPD tente d'accroitre sa capacité de concevoir de nouvelles protéines
et de s'aventurer à modifier fondamentalement la façon dont les médicaments, les vaccins, les carburants et les nouveaux matériaux sont fabriqués.
Encore faut-il bien connaître l'aventure du Covid-19, ses origines et son histoire d'une part pour mieux en comprendre ses processus de vie et de survie qui le motivent à s'installer et se développer comme d'autres de ses semblables dans l'espèce humaine et les autres espèces intermédiaires, et d'autre part d'en trouver les stratégies contradictoires qui le condamnent à aller ailleurs ou pas et sans nuire à l'humanité. D'où le besoin de capteurs de virus avant d'entrée dans le corps humain (systèmes respiratoire et digestif) pour modifier son comportement et les expulser, et dans le corps humain pour les détruire en quantité suffisante pour laisser le système hymunitaire apprendre de leurs structures et fonctions afin d'en générer des anticorps dès plus efficaces.
Le CREDACI GBM-LAB tente d'apporter des solutions en créant des concepts et modèles mathématiques
tenant compte de la diversité dans l'identitaire où l'équivalence n'est pas l'égalité, ni le raprochement immédiat à l'identitaire abandonnant sa diversité,
mais la texture des identitaires dans leurs diversitaires pour former un identitaire plus vaste et plus riche optimisant les excès sans exclure les distorsions, et forme un moule souple propice à l'intégration d'un plus grand nombre de formes imbricables et intricables (... pour l'intérêt général et individuel).
tenant compte de la diversité dans l'identitaire où l'équivalence n'est pas l'égalité, ni le raprochement immédiat à l'identitaire abandonnant sa diversité,
mais la texture des identitaires dans leurs diversitaires pour former un identitaire plus vaste et plus riche optimisant les excès sans exclure les distorsions, et forme un moule souple propice à l'intégration d'un plus grand nombre de formes imbricables et intricables (... pour l'intérêt général et individuel).
A l'aide des Texturologies Quantiques Prétopologiques, le High Parallel Computing (HPC) utilisant les Bits-Computers
devient un High Parallel Quantum Computing (HPQC) avec les QBits-Computers
puis un Huge Parallel Texturology Quantum Computing (HUPTQC) avec les TQBits-Computers
et un Huge Parallel Optical Texturology Quantum Computing (HUPOTQC) avec les OTQBits-Computers (Optical Texturology QBits)
Avec myQLM d'ATOS,
nous préparons les NoteBooks myQLM de programmation quantique texturologique
The Atos Quantum Learning Machine (QLM & QLM E) is an enterprise-class solution
for quantum simulation that extends the capabilities of myQLM.
Avec Wolfram Mathematica les NoteBooks sont générés automatiquement à partir du calcul et de la programmation.
With the Jupyter notebooks, an open-source web application
that allows you to create and share documents that contain live code, equations, visualizations and narrative text
we prepare data cleaning and transformation, numerical simulation, statistical modeling, data visualization, machine learning and IA.
and With Binder, open those notebooks in an executable environment,
making your code immediately reproducible by anyone, anywhere.
https://gke.mybinder.org/
after enter your repository information by providing in the above form a URL or a GitHub repository that contains Jupyter notebooks,
as well as a branch, tag, or commit hash. Launch will build your Binder repository.
If you specify a path to a notebook file, the notebook will be opened in your browser after building.
A partir des travaux
sur la Trans-combinatoire et les Textures Prétopologiques et Quantiques et leurs Texturologies ainsi que les Processus Markoviens Prétopologiques
associés à l'Algèbre des Quinternions et à la Théorie des Sous-ensembles superposés et intriqués du Résualisme et de la Cybericité Sont préparés avec Mathematica, des outils d'IA et DeepLearning, classification multi-hierarchique et multi-paramétrique, avec représentation 2D et 3D interactives en temps réel par DataMining avec simulateur de vol dans les données en Réalité Virtuelle et Augmentée, et algorithmique de Trans-Combinatoire (3^(n-1) + 1 possibilités en parallel au lieu de 2^n), de Textures et Texturologies Quantiques Prétopologiques Relationnelles.