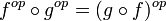La texture quantique relationnelle prétopologique
dans les systèmes
complexes évolutifs
Réflexions liées
au séminaire de
Mathias Béjean sur
l'Approche catégorique des processus de conception et d’innovation
collectives
Séminaire MaMuPhi du 7 Décembre 2013, de 10h30 à 13h,
Patrick SAINT-JEAN
http://patricksaint-jean.fr/, http://patrick.saintjean.free.fr
Nouvelles Technologies et Création, ArtsAps, Master Design
CREDACI (Centre de Recherche et d'Etude en Design Arts et Création Industrielle)
UCVI (Univers Cités Virtuelles Interactives)
Ecole Normale Supérieure, Département Design, Sciences Humaine, Cachan,
Docteur en Biologie de l'Université de Paris XIII,
Ingénieur en Informatique-Electronique-Automatique de l'ESIEA
Conférence répertoriée au Archive for Mathematical Sciences & Philosophy
Partant d'une part des travaux de Mathias Béjean
sur l'Approche catégorique des processus de conception et d’innovation collectives donnant l’état d’avancement d’un travail mené en collaboration avec A.C. Ehresmann et visant à développer une approche des processus de conception et d’innovation collectives fondée sur la Théorie des Catégories. A ce titre, le travail mobilise la notion de « MES » (Ehresmann et Vanbremeersch 2007) qui propose une méthodologie catégorique particulière permettant d’intégrer le Temps pour analyser des systèmes évolutifs à mémoire. L’exposé introduit un MES particulier, nommé D-MES, et y formalise, notamment, les notions de « situation », d’ « action » et d’« innovation » pour un système de conception quelconque pouvant impliquer des composants hétérogènes, humains et non humains, en interaction. La cohérence interne de ce cadre, ainsi que la manière spécifique de traiter la dynamique et la mémoire d’un tel système, permettent alors d’éclairer plusieurs difficultés de conceptualisation du travail de conception à l’œuvre et de revenir, notamment, sur certains dualismes aporétiques dans ce champ disciplinaire (ex. : un/multiple, opération/structure, global/local, connu/inconnu…). Dans une tradition « MaMuPhique », l’exposé se terminera par une réflexion sur le rôle des mathématiques dans ce travail et d’éventuelles « raisonnances » philosophiques.
et d'autre part des travaux de Patrick Saint-Jean (1967-2013)
sur l'Approche des structures algébriques et topologiques en Théorie des Catégories dans le Design des espaces mathématiques hétérologiques et hétéromorphiques lié à la non-transitivité, où il est intéressant d'ouvrir les structures topologiques à la prétopologie d'Alexander Grothendieck et de Marcel Brissaud pour s'apercevoir d'une part que tout est fondé sur l'homomorphisme, l'homologie et la transitivité, et d'autre part qu'il existe dans des travaux parallèles de l'auteur depuis 1967 des notions particulières de « trans-combinaison » et « prétopologie » dès 1971 qui font évoluer le Design des espaces mathématiques vers des systèmes dynamiques où les notions de non-transitivité, d'hétérologie et l'hétéromorphisme ont du sens et introduisent les textures prétopologiques relationnelles (sonores et visuelles au départ, puis généralisées) et les texturologies quantiques relationnelles prétopologiques qui s'avèrent propice à la recherche d'esthétiques musicales, visuelles et conceptuelles, tant dans les systèmes statiques que dynamiques et évolutifs.
Après avoir ajouté au "Théorème du sandwich au jambon" d'Hugo SteinHaus repris par Stephan Banach (1938) en Topologie, le "Théorème de la soupe de légumes" (PSJ, 2012) en Prétopologie pour ne plus avoir peur du mélange, de l'amalgame, des co-polymères et des dissonances, il est possible de rajouter le "Théorème de la jardinerie" en Texturologie Prétopologique Quantique Relationnelle des Systèmes évolutifs.
Introduction
Une réalité pratique : Formalisation des activités d'une Jardinerie par MB :
"As other design disciplines, garden
design is composed of several design stages starting from client needs
expression to site survey, conceptual design, planning and
implementation. In the studied agency, a typical design project thus
often started with a client expressing desired proprieties about plants
or shrubs, especially in terms of colours and forms, often resulting in
the designating of a specific botanic variety (e.g. “I love roses”).
The client then often asked technical questions about sun exposition or
soil requirements regarding the mentioned plants. During this phase,
the designer-in-chief listened to the client, answered to the technical
questions but progressively also interrogated the client more generally
about the desired proprieties. In particular, she started asking
questions about the signification of these proprieties for the client
which results in formulating a provisory interpretation, for instance:
“In fact, you’re looking for liveliness.” Based on this reformulation,
the client reacted differently as “liveliness” did not directly match
with his understanding of flowerbeds or mix boarders. Then the designer
brought the clients to a place in which she had a collection of rare
plants and started to sensitize her client to new aspects of garden
design, including textures, effects of lights or sounds. With time
going, a significant change in the way clients were speaking of their
garden project always occurred. For instance, while often ignoring
these aspects at the beginning of the project, they started operating
new formulations on textures with an increasing level of complexity.
Such evolution made it possible for many of them to take part to the
conceptual, the planning and the implementation phases of their garden
design project.
To model the design system of this illustration, we here only consider
2 design actants: the client and the designer-in-chief, and their
current environment, but other components could be integrated to the
analysis. First, this means characterizing all the operations of the
considered client in its internal mental space to form his local
landscape Lc: (i) using his or her previous knowledge on plants and
gardens (retrospection); (ii) imagining a future garden or nice
flowerbed among other alternatives in his own landscape (prospection);
(iii) selecting procepts to formulate and communicate (e.g. with words,
gestures, drawings, photographs) desired proprieties on this still non
existing garden or flowerbed to the designer (virtual
complexification). Second, this means characterizing all the operations
of the designer-in-chief in her own mental space to form her own
landscape Ld: (i) collecting the information given by the client and
using her knowledge to remember plants that have the desired
proprieties as well as preceding experiences with them and their
aesthetic effect, for instance by relying on the concept of
“liveliness” (retrospection through abduction); (ii) figuring different
design strategies (procepts) out in relation with the design goal and
selecting one of them, for instance by gathering specific textures to
evoke a “liveliness effect” (prospection); (iii) reformulating the
client “brief” in terms of the selected strategy, for instance by
giving concrete examples of textures that could produce “liveliness”
(complexification through materialization).
Third, this means characterizing the operations that made it
progressively possible for both client and designer not only to operate
separately, namely from an individual mental point of view in their
local landscapes, but to operate jointly by forming a global landscape
where new compositions (or decompositions) of abstract or concrete
objects and strategies will be selected from a situated and social
point of view."
Une réalité théorique : Formalisation par MB d'un système évolutif à partir des travaux de Andrée Ehresmann and Vanbremeersch 2007 sur les MES (Memory Evolutive Systems) :
Mathematical notions and basic
definitions
1. A category is a directed (multi-)graph K equipped with an internal
(partial) composition which maps a path (f, g) from A to B on an arrow
fg from A to B; it is associative and each object has an identity; a
vertex is called object, and an edge morphism (or 'link').
2. A functor F from K to a category K' maps an object A of K to an
object FA of K', a link f: A → B on a link F(f): FA → FB, and preserves
the composition.
3. A pattern (or diagram) P in a category K consists in a family of
objects (Pi)i and distinguished links between them (in K). A collective
link (or inductive cone) from P to C is a family (si: Pi →C)i of links
of K well correlated by the distinguished links of P.
4. P admits a colimit cP in K if there is a collective link from P to
cP through which any other collective link from P to an object C
factors uniquely.
5. K is hierarchical if the class of its objects is partitioned into a
finite number of complexity levels 0, 1, 2, etc, so that an object C of
level n+1 is the colimit of at least one pattern P with each Pi of
level < n+1. Then C also admits at least one ramification obtained
by taking a lower level decomposition P of C, then such a decomposition
of each Pi and so on down to level 0. The complexity order of C is the
smallest length of one of its ramifications
6. An Evolutive System (ES) K is a family (Kt)t of categories and
partial 'transition' functors between them satisfying a transitivity
condition; a component of the system is a maximal family of objects of
the Kt related by transitions. K is a Hierarchical Evolutive System
(HES) if the categories Kt are hierarchical and the transitions respect
the level.
7. A component C of the HES K is multifaceted if it admits at least two
lower level decompositions which are not isomorphic nor connected by a
cluster of links between their components. K satisfies the Multiplicity
Principle if K admits such multifaceted components. In this case
besides simple links from A to C which bind clusters of links between
decompositions Q of A and P of C, there are complex links obtained by
composing simple links binding non adjacent clusters (cf. Figure 2).
8. Emergence Theorem. The Multiplicity Principle is necessary for the
existence of components of complexity order > 1. It allows the
emergence of components of increasing complexity order through
successive complexifications.
9. In a MES, the landscape of a co-regulator CR at time t is the
category Lt whose objects are the clusters of links from a component to
CR which are active during the step beginning at t.
10. Iterated Complexification Theorem.Two successive complexifications
of a category satisfying the multiplicity principle cannot be reduced
to a unique complexification. (The proof relies on the role played by
the complex links emerging in the first complexification.)
Un Design d'Espaces Mathématiques
Une logique hexagonale
L'hexagone logique (également appelé hexagone d'opposition) met en évidence des connexions entre six types d'assertions qui sont reliées entre elles par leurs valeurs de vérité. C'est une extension du carré logique d'Aristote découverte de façon indépendante à la fois par Augustin Sesmat et par Robert Blanché qui consiste à introduire deux nouvelles connexions Y et U, Y étant la conjonction de I et O tandis que U est la disjonction de A et E.
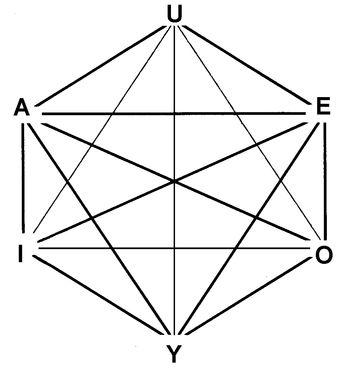
L'hexagone logique de Robert Blanché et la Logique de Jean-Yves Béziau
A est interprété comme la nécessité
E est interprété comme l'impossibilité
I est interprété comme la possibilité
O est interprété comme la non nécessité
U est interprété comme la non contingence
Y est interprété comme la contingence


Hexagone et Cube logique d'un objet boroméen de René Guitar
Automate fini selon
Wolfram :
Une logique trans-combinatoire selon
Patrick Saint-Jean
Des dés non transitifs sont un ensemble de dés où, si un premier dé a plus de chances de donner un plus grand résultat qu'un deuxième et si celui-ci a plus de chance qu'un troisième, ce dernier peut tout de même avoir plus de chance de l'emporter sur le premier. En d'autres termes, la relation « a une plus grande probabilité de donner un plus grand nombre » n'y est pas transitive.

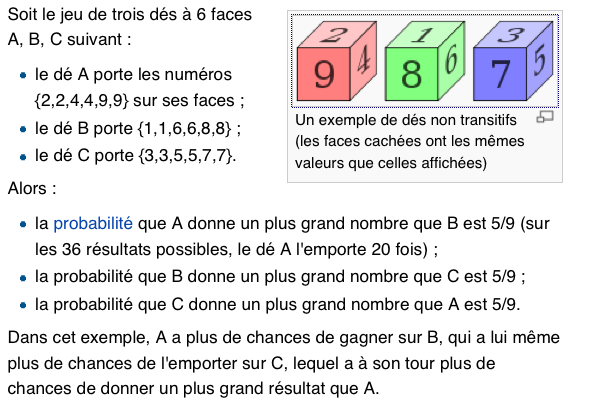

Cette situation est similaire à celle du jeu pierre-feuille-ciseaux où chaque élément gagne par rapport à l'un des deux autres et perd par rapport au dernier.
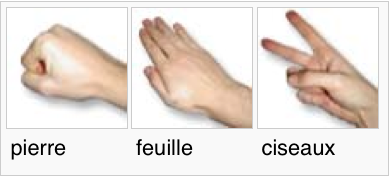

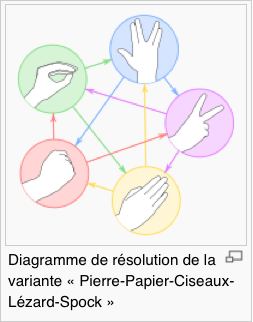
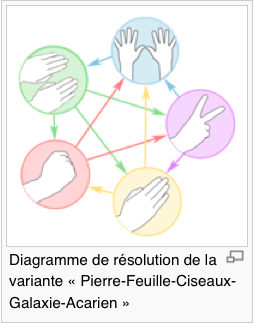
Graphes et Fermeture transitive

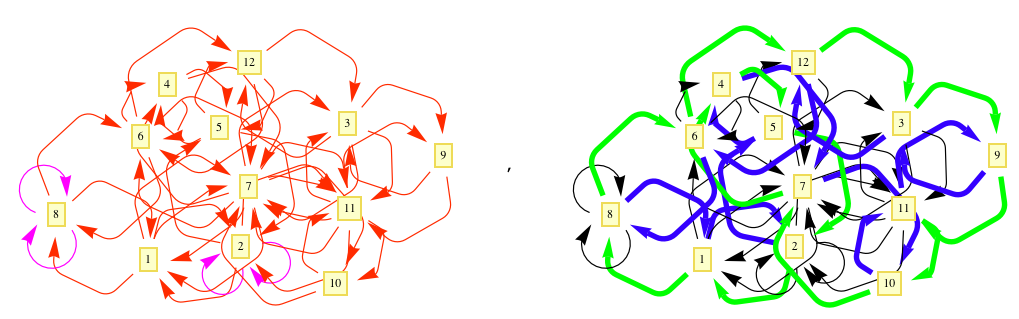
La Jardinerie du Parc de
Sceaux

Parc de Sceaux : l'avant 2012 (création vivante évolutive de la
diversité) et l'après (création stérile statique vouée à Le Notre).
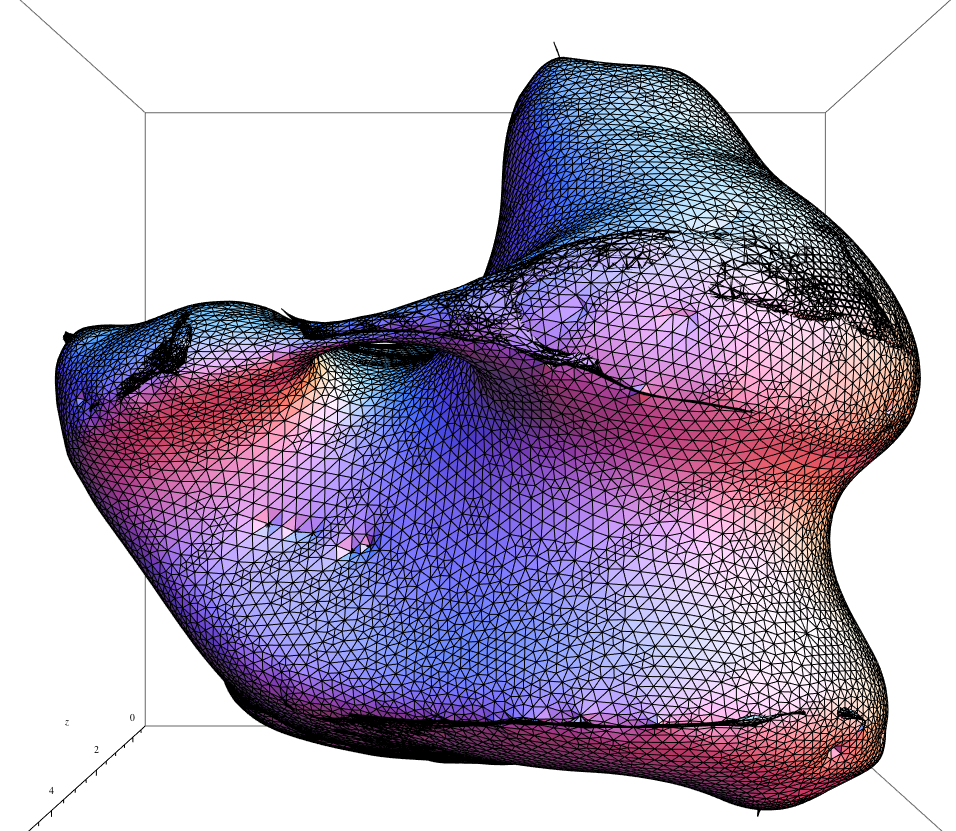
Les fonctions d'onde de la Texturologie quantique relationnelle
prétopologique sont plus complexes.
On peut imaginer que chaque sommet ou chaque arrête est une équation
hétérologique.
Chaque sommet peut être un processeur qui calcule (arytmétique et
logique) la position relative dans la structure ou sa couleur locale
(propriété résultantes de la composition de relation).
Le HPC (High Parallel Computing) sera peut être en mesure de nous le
dire ?
Nous ne manquerons pas également de
faire appel aux philosophes qui d'une part ont jalonnés ces travaux
et servis d'ancrage esthético-philosophique en Mental-Design,
Thinking Design et Behavioural Design lié au Digital Design et
Design numérique à travers le Design du concept multimédia et
polyagogique : de Parménide et Bergson dans les années 60, à
Gilles Deleuze
et Félix Guattari, Jacques Derrida, Gilles Chatelet et Alain Badiou
très actuels, et d'autre par sont en bouclage rétroactif avec Kurt
Gödel et Douglas
Hofstadter, Pierre Bourdieu, Edgard Morin, Michel de Certeau, Edouard
Glissant et même Jean-Michel Lucas dans son organisation de la
palabre, et Wittgenstein dans son désire de voir et d'entendre, dont
nombreux décrivent des situations très complexes mais malheureusement
s'arrête à la fermeture topologique donc avec des raisonnements
homologiques, homomorphiques et transitifs pour ne pas désacraliser
notre culture faite d'ordre et de classe d'équivalence en oubliant le
reste du monde plus conséquent ou en faisant comme si il n'existait pas
ou comme si il était comme leur propre monde.
Recherche et Développement
Démarche et méthode
Partant du livre de vulgarisation scientifique de Douglas Hofstadter : "Gödel Escher Bach, les Brins d'une Guirlande Eternelle", 1979, Basic Book Edition ; traduction française, 1985, InterEdition, qui obtint le prix Pulitzer en 1980 :
"Si la consistance est la condition minimale pour que les symboles acquièrent des significations passives, la notion complémentaire, la complétude, est la confirmation maximal de ses significations passives. ("capable d'être" ou "pouvant être")
Alors que la consistance d'un système formel est la propriété selon laquelle "toute assertion engendrée par le système est vraie", la complétude est l'inverse : "Le système engendre toute assertion vraie"... pour le domaine qu'on tente représenter dans le système formel.
La complétude se traduit ainsi :
"Toute assertion vraie qui peut être exprimée au moyen des symboles du système est un théorême". ...
"Si le système est non contradictoire, mais incomplet, il y a une mauvaise correspondance entre les symboles et leurs interprétations respectives ...
Parfois en "élaguant" quelque peu les interprétations, on peut parvenir à la complétude du système." (réductionnisme).
Mais en rajoutant une règle suplémentaire (inflationisme, expansionniste, entropique) pour assurer la complétude du système, on constate souvent qu'on ne l'obtient pas, car une brisure déductioniste de la chaîne directe ajoute des rétroactions (feedback) non convergente, qui "perturbent" et créent des systèmes bouclés parfois indécidables ou un anneau de Möbius (à la fois dessus et dessous), une bouteille de Klein (à la fois intérieur et extérieure), et un Escalier de Escher (monter plus bas qu'on est et descendre plus haut) qui sont topologiquement correctes comme surface de dimension N relatant d'un espace N+1, mais qui restent le symbole du cheminement logique qui amène à la contradiction créant le paradoxe à cause du déphasage à la jointure bouclée mais qui peut se satisfaire avec un CQFD et retour au départ.
Il nous faudra donc prendre toutes les précautions.
Mais sans oublier Nietzsche : « Je vous le dis, il faut avoir encore du chaos en soi pour enfanter une étoile dansante. »
Ainsi :
Le théorème de Gödel affirme qu'il restera toujours des énoncés indécidables (tant que la théorie reste récursivement axiomatisable).
Et par conséquent :
"Dans n'importe quelle théorie récursivement axiomatisable, cohérente et capable de « se formaliser », on peut construire un énoncé qui ne peut être ni prouvé ni réfuté dans cette théorie."
Les nouveaux énoncés viennent régulièrement non pas remettre en question les fondements mathématiques mais à les préciser et élargir la base de plus en plus prêt de la "Nature" (dans un cosmos), dont l'Être et l'essence de sa pensée dans son expression et sa poïétique (processus de création).
Et par conséquent lui donne un fondement également philosophique et artistique d'une pensée en devenir, d'une "virtualité jouissive ou jubilatoire" que Chatelet aurait rajoutée à sa virtualité physico-mathématique.
Les nouveaux énoncés, qui nous intéressent, concernent la notion de Prétopologie associée à la Topologie pour en faire une Topologie augmentée.
C'est aussi s'interroger en ce que l'incomplétude des uns peut être l'essentiel des autres, et faire la différence complémentaire qui elle même à ses propre incomplétudes.
Et qu'une incomplétude soit objet d'une catégorie, et "prendre son sens comme symbole d'une autre théorie complémentaire" n'est pas en soi une impossibilité.
Dans cette exposé la philosophie sert de starter, d'initiateur à une recherche et développement mathématique pour aboutir à une composition musicale et visuelle avec moteur sémantique dans un Design du Concept Multimédia en PolyAgogic CyberSpace pour le spectacle de la connaissance dont le Chef d'orchestre devient le K-J ou Knowledge-Jockey pour développer le KJing.
Une philosophie naîtra sans doute de cette théorie mathématique. Celle qui est pour nous déjà le Résualisme de la Cybéricité, philosophie relationnelle de la différence (et pas seulement de l'identité et de la différentiation).
Partant d'un structuralisme mathématique qui nous mène à la Théorie des Catégories, nous tenterons, en passant par les Structures topologiques et prétopologiques, une avancée vers une Théorie structuro-fonctionnelle-systémique par des Précatégories et préfoncteurs hétéromorphiques.
Les Structures
Une structure désigne toute théorie « plus forte » que la théorie des ensembles, c'est-à-dire une théorie qui en contient tous les axiomes, signes et règles.
C'est donc une théorie « fondée » sur la théorie des ensembles, mais contenant également des contraintes supplémentaires, qui lui sont propres, et qui permettent également de définir de nouvelles structures qu'elle inclut. Cette notion est ainsi une puissante contribution à l'hypothèse selon laquelle la théorie des ensembles fournit le fondement des mathématiques.
Ce terme est à l'origine de ce que l'on a appelé le structuralisme mathématique.
Un morphisme ou homomorphisme est une application entre deux ensembles munis d'une même espèce de structure, qui respecte cette structure. Cette notion de morphismes est fondamentale en mathématique. Elle permet de comparer et de relier les objets mathématiques entre eux.
Un morphisme de structure transporte la loi de structure, et va ainsi conserver toutes les propriétés liées à cette loi. Il est donc intéressant d'étudier comment se comportent les principaux objets de la théorie des structures par les morphismes.
La notion de morphisme est un des concepts de base de la théorie des catégories, où on lui donne un sens bien plus large. Ainsi, un morphisme n'est pas forcément une application, c'est juste une flèche reliant deux objets qui ne sont pas forcément des ensembles : la flèche peut relier deux structures d'une même espèce, par exemple deux groupes ou deux espaces vectoriels.
Les morphismes ont des applications particulièrement importantes en physique moderne, en particulier la mécanique quantique.
Nous verrons alors comment à partir d'un structuralisme hétéromorphique nous cherchons une texture prétopologique et une texturologie quantique prétopologique relationnelle d'une autre nature mais qui se retrouve dans une Topologie augmentée utilisant des andromorphismes (hétéro et homo morphisme).
Prétopologie selon Marcel Brissaud et le groupe Z. Belmandt,repris par l'association Pretopologics
Longtemps les ensembles ont été considérés comme un monde de patatoïdes, un peu comme des météorites galactiques (des sacs de marrons ou boîte d'allumettes pour les enfants).
La physique les a peuplés de particules et de molécules (Atomium) et de galaxies.
La théorie de l'information les met en réseaux de réseaux que la théorie des graphes habille en nœuds, arrêtes ou sommets, mis en relation par des liens ou arcs, (ponts, passerelles ou bords à tirer), formant des parcours (chaînes, cycles, chemins ou circuits), mais aussi des structures.
En topologie algébrique, si les graphes représentent un ensemble de même propriété, de même nature, les paramètres mis en jeu seront des quantités de pondération des nœuds et de liens, mis en relation par des formules (sommes pondérées, etc.)
En topologie, proprement dit, se sont les relations entre noeuds créant des structures particulières, engendrant des fonctionnalités statiques ou dynamiques particulières .
Et les degrés de proximités successives ou de positions relatives entre-eux vont prendre de l'intérêt.
On voit bien que se sont les classes d'équivalence et d'ordre qui organisent les structures.
Et tout graphe de sommets variés est décomposé en sous graphes connexes superposés.
Nous utiliserons les travaux exprimés par Vincent Levorato dans sa thèse de 2010 en informatique : Contributions à la Modélisation des Réseaux Complexes : Prétopologie et Applications.
Nous y retrouvons les définitions explicitées dans les ouvrages de Prétopologie chez Hermès (1993) et Hermann (2009).
Ainsi :
« L’historique de cette idée débute dans les années 20 quand Fréchet visait à construire une topologie ayant moins d’axiomes [33]. Puis Appert reprit ces travaux dans les années 30, suivi par Monteiro dans les années 40 puis par Ky-Fan. Dans les années 60, Cech décrivait dans son ouvrage des structures topologiques privées de l’axiome idempotence [20]. C’est au début des années 70 que des chercheurs français (Marcel Brissaud, Gérard Duru, Jean-Paul Auray, Michel Lamure [...] pour ne citer qu’eux) débuteront leurs travaux sur la prétopologie et comment trouver une formalisation du concept de proximité, afin de résoudre des problématiques difficiles liées à la contrainte de l’outil mathématique utilisé, ici la topologie. Dans le cadre de mes travaux, la prétopologie est à mon sens l’outil permettant d’aller plus loin que la théorie des graphes habituellement utilisée pour représenter les réseaux. Son cadre général, ainsi que sa capacité à représenter la dynamique d’un système en font l’outil adéquat pour la modélisation des réseaux complexes. Dans cette partie, des définitions liées à la prétopologie sont données, ainsi qu’une définition générale d’un réseau. Nous proposerons ensuite des choix de structures de données adaptées dans le but de limiter la complexité des opérations afin de pouvoir construire des simulations exploitables, que nous appliquons sur plusieurs problématiques ».
La théorie de la prétopologie
Cette section énonce les définitions de la prétopologie utilisées pour les travaux de recherche présentés dans ce mémoire, l’ouvrage de référence [7] contenant une présentation exhaustive de la prétopologie.
[7] Z. Belmandt. Manuel de prétopologie et ses applications : Sciences humaines et sociales, réseaux, jeux, reconnaissance des formes, processus et modèles, classification, imagerie, mathématiques. Hermes Sciences Publications, 1993.
Espace prétopologique
Soit E un ensemble non vide, et soit P(E) l’ensemble des parties de E.
Définition de l'adhérence
Soit une application a : P(E) → P(E) appelée adhérence et définie comme suit :
∀A, A ⊆ E l’adhérence de A, a(A) ⊆ E est telle que :
-
a(∅) = ∅ (P1)
-
A ⊆ a(A) (P2)
L’adhérence est associée au processus de dilatation.
De plus, a(.) peut être appliquée à A selon une séquence : A ⊆ a(A) ⊆ a2(A) ⊆ ... .
Cela signifie que l’on peut suivre le processus pas à pas, ce qui n’est pas possible avec la topologie,
qui conserve la propriété d’idempotence (a(A) = a2(A)) [17].
Grâce à l’adhérence, on peut directement modéliser la notion de proximité. En terme de complexité, le coût d’une adhérence sera étudié lors de la partie concernant les structures de données utilisées en prétopologie.
Définition de l'intérieur
Soit une application i : P(E) → P(E) appelée intérieur et définie comme suit :
∀A, A ⊆ E l’intérieur de A, i(A) ⊆ E est telle que :
– i(A) = [a(Ac )]c (P1)
– i(A) ⊆ A (P2) avec A c le complémentaire de A soit E − A.
L’intérieur est quant à lui associé au processus d’érosion.
Notons que la propriété 1 de l’intérieur amenant la dualité n’est pas toujours vraie.
Il est possible de définir une application intérieur indépendamment de l’adhérence.
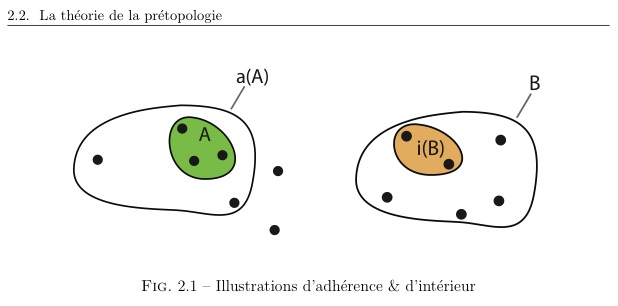
Dans le Z. Belmandt (Hermes, 1993, p 25-30), qui rappelle un peu la morphologie mathématique de Matheron et Serra, l'adhérence est définie par un processus d'extension (dilatation) de P(E) → P(E) tel que ∀A appartenant à P(E), a(A) inclu A.
Un autre processus dual dit d'érosion définit l'intérieur i de P(E) → P(E) tel que ∀A appartenant à P(E), i(A) est inclu dans A.
On appelle espace prétopologique le triplet (E,i,a) dont les applications i et a sont définies précédemment.
Fermés et Ouverts, Fermeture et Ouverture
Le processus de dilatation généré par l’adhérence s’arrête à un instant donné et n’évolue plus. Dans ce cas, on a ak+1(A) = ak(A). On nomme A comme étant un sous ensemble fermé. De la même manière, l’évolution de l’intérieur va cesser, ce qui nous donne ik+1(A) = ik(A). Cette fois, on nomme A comme étant un sous ensemble ouvert.
Respectivement, on utilise les notations F(A) pour la fermeture de A et O(A) pour l’ouverture de A. La complexité d’un fermé, si on prend l’adhérence comme opération de base, se fait au pire en O(n × coût d’une adhérence).

Fermés élémentaires et fermés minimaux
On appellera fermé élémentaire et on notera Fx, la fermeture d’un singleton {x} de E. On note Fe(E, a) ou Fe, l’ensemble des fermés élémentaires de E :
L’algorithme (Alg. 2.2.3) permet le calcul de la famille des fermés élémentaires , et si on prend comme opération de base l’adhérence, la complexité de cet algorithme qui comprend deux boucles imbriquées est, dans le pire des cas, en O(n2 × coût d’une adhérence).
On appelle fermé minimal de E, tout élément de F(E,a), minimal au sens de l’inclusion. L’ensemble des fermés minimaux est noté : Fm(E,a) ou Fm. Un résultat important est que tout fermé minimal est obligatoirement élément de Fe, c’est à dire un fermé élémentaire. Déterminer les fermés minimaux revient donc à explorer les éléments de Fe et en extraire les éléments minimaux par la relation d’inclusion. L’algorithme [15] permettant le calcul de la famille des fermés minimaux (Alg. 2.2.3), comprend également deux boucles imbriquées, donc la complexité dans le pire des cas est en O(n2) (l’adhérence n’intervient pas dans ce cas).
Espace prétopologique de type V
Un espace prétopologique général comme défini ultérieurement ne présente que peu d’intérêt en l’état, car il est difficile d’en faire une analyse.
Il faut donc amener une nouvelle propriété pour rendre cet espace prétopologique plus «intéressant», d’où la définition d’un nouvel espace prétopologique : le type V.
Un espace prétopologique de type V (E,i,a) est défini comme suit :
∀A, B, A ⊆ E, B ⊆ E et A ⊂ B avec a(A) ⊆ a(B)
∀A, B, A ⊆ E, B ⊆ E et A ⊂ B avec i(A) ⊆ i(B)
D’autres types d’espaces existent :
Espace prétopologique de type Vd
Un espace prétopologique de type Vd (E,i,a) est défini comme suit :
∀A, B, A ⊆ E, B ⊆ E et A ⊂ B avec a(A ∪ B) = a(A) ∪ a(B)
∀A, B, A ⊆ E, B ⊆ E et A ⊂ B avec i(A ∩ B) = i(A) ∩ i(B)
Tout espace de type Vd est de type V.
Espace prétopologique de type Vs
Un espace prétopologique de type Vs (E,i,a) est défini comme suit :
∀A, A ⊆ E, avec a(A) = ∪ a({x}) ∀ x∈A
Un espace de type Vs est clairement de type Vd.
Les applications a et i ne sont pas forcément idempotentes.
On ne doit pas confondre une prétopologie de type Vs et une topologie.
Les types d’espaces les plus utilisés dans nos études sont les types V et Vs .
Préfiltre et base de voisinage
Comme écrit plus haut, le concept de proximité en prétopologie est fondamental, c’est pour cela qu’il nous faut définir ce que l’on appelle «être proche » d’un élément, autrement dit être dans le voisinage de cet élément. Pour cela il faut définir ce voisinage par un préfiltre et une base de voisinage.
Préfiltre
Une notion essentielle de la topologie est la notion de filtres, qui conduit à celle de voisinage. En prétopologie, non seulement nous conservons cette notion, mais nous définissons en outre celle de préfiltre.
Une partie F de P(E) est un préfiltre sur E si elle vérifie la propriété de stabilité par passage à tout sur-ensemble :
∀ F ∈ F,∀ H ∈ P(E), F ⊂ H ⇒ H ∈ F Soit (E,i,a) un espace prétopologique de type V.
Pour tout x de E, on définit le préfiltre V (x) de parties de E par :
V(x)={V ⊆ E/ x∈i(V)} Les éléments de V(x) sont appelés voisinage de x.
Pour comprendre la relation avec les applications adhérence et intérieur, on les définit à partir d’un préfiltre V(x) :
a(A)={x∈E/ ∀V, V ∈V(x),V ∩A ≠ ∅}
i(A)={x∈E/ ∀V, V ∈V(x), V ⊆A}
Base de voisinage
Soit B(x) la base de V(x) définie comme suit :
∀ V, V ∈ V(x), ∃B, B ∈ B(x), B ⊆ V
On définit ainsi l’adhérence comme suit : a(A) = {x ∈ E/ ∀ B, B ∈ B(x), B ∩ A≠ ∅}
Il existe plusieurs manières de définir la base de voisinage selon la problématique étudiée.
Par exemple, dans [52], on définit une population où les éléments sont reliés par une ou plusieurs relations binaires Ri réflexives, soit pour tout i, la partie Bi(x) étant construite pour chaque x appartenant à E de la manière suivante :
Bi(x) = {y ∈ E/ x Ri y}.
Un autre cas tiré de [48] où E est doté d’une métrique définie par une distance et où la base de voisinage pour chaque x appartenant à E et r ∈ R+ est définie comme suit :
B(x,r) = {y ∈ E, d(x,y) ≤ r}
Modélisation d’un réseau par la prétopologie
Il y a plusieurs raisons pour utiliser la théorie de la prétopologie dans la modélisation des réseaux : les modèles utilisant la théorie des graphes ont certaines limites.
- Premièrement, on ne peut pas dissocier les liens : orientés ou non, ils sont tous de nature identique. Si l’on veut utiliser n différentes relations entre les noeuds, il faut construire n graphes différents ce qui semble peu pratique [54].
- Deuxièmement, tous les modèles utilisant la théorie des graphes présentés jusqu’alors dans les études récentes ont au moins une propriété qui ne correspond pas aux réseaux du réel [56].
- Et troisièmement, les relations se font par paires de noeuds, on ne peut donc pas avoir de relations entre un groupe de noeuds et un noeud par exemple.
Les hypergraphes répondent à ce problème, mais sont un cas particulier d’espace prétopologique [7].
Où les autres modèles ont échoué, la théorie de la prétopologie peut apporter une réponse.
Définition d’un réseau en prétopologie
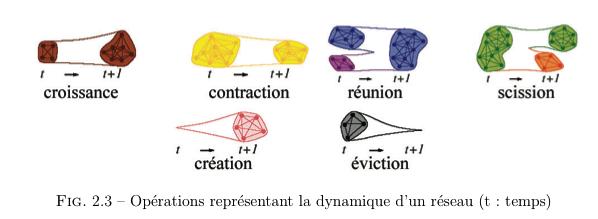
Un réseau peut être défini comme une famille de relations binaires ou valuées définies sur une population donnée [24].
La dynamique du réseau est basée sur des opérations telle que l’arrivée de nouveaux éléments, l’éviction d’éléments existants, la formation de groupe ou la séparation en sous-groupes (voir Fig. 2.3). Ces phénomènes sont souvent observables dans les réseaux sociaux sous forme de communautés [5] mais également dans le cas des réseaux de manière plus générale.
Dans le cadre de la prétopologie, un réseau est une famille de prétopologies sur un ensemble donné [23], d’où la définition suivante :
Soit X un ensemble : soit I une famille dénombrable d’indices ; soit {ai, i ∈ I} une famille de prétopologies sur Xi ; la famille d’espaces prétopologiques {(X, ai), i ∈ I} constitue un réseau sur X.
Structures de données adaptée à la prétopologie
Comme précisé précédemment, les deux types d’espaces prétopologiques qui nous intéressent sont le type V et le type Vs. Ces deux espaces ne sont pas tout à fait basés sur le même type de structure de données. Mais quelle structure de données serait assez efficace pour permettre des opérations rapides sur de tels espaces ? A notre sens, la structure de données la plus efficace est la table de hachage.
Modélisation des réseaux complexes par la théorie des graphes
Coefficient de regroupement, assortativité et d’augmentation d’un graphe.
Le coefficient de regroupement C également appelé ”clustering coefficient” est la probabilité que deux voisins d’un sommet donné soient voisins entre eux. Cela correspond à la densité locale d’un sommet. Soit di le degré d’un sommet i,
C(i) = 2 × |nbre de liens entre les voisins de i/ di(di − 1)
Le degré de corrélation se calcule grâce à la moyenne des degrés des voisins d’un noeud. Pour faire simple, cela répond à la question : est-ce que dans un réseau, les sommets ayant un degré élevé sont de préférence connectés à d’autres sommets avec un degré élevé, ou sont plutôt connectés à des sommets ayant un faible degré ?
Degré moyen des voisins d’un sommet i (avec arêtes pondérées) :
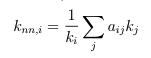
Assortativité d’un graphe :

Un graphe augmenté G = (V,E,E′) est un graphe obtenu à partir d’un graphe H = (V,E), en ajoutant un ensemble d’arêtes supplémentaires E′ sur V . La distance sous-jacente de u à v dans G est la distance de u à v dans H.
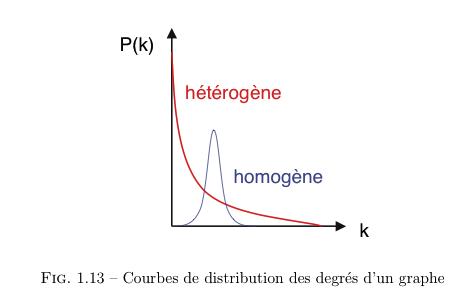
Pour finir, on analyse souvent la distribution des degrés des sommets d’un graphe (Fig. 1.13). Deux distributions de degrés sont connues :
– une distribution homogène des degrés des noeuds (selon une loi de Poisson) – une distribution hétérogène des degrés des noeuds (selon une loi de Puissance)
Espaces de Texture Prétopologique selon Patrick Saint-Jean
Dès 1967, Patrick Saint-Jean développe des travaux en Musiques Formelles (Iannis Xenakis) où il se confronte à des problèmes de combinatoire et de permutation en architecture sonore qui ne satisfont pas à ses problématiques de texture sonore, timbrale et orchestrale. Il montre qu'il existe des trans-combinaisons, combinatoire entre des ensembles de natures différentes ou d'un ensemble avec son environnement, fondées sur la représentation du cube dans la n-ième dimension, alors que la combinatoire est fondée sur la représentation du triangle dans n-ième dimension (triangle de Pascal).
Parallèlement une « texturologie prétopologique » va se mettre en place entre Patrick Saint-Jean et le berceau lyonnais : en 1971, Jean-Pierre Landrieu, professeur de mathématique à l'ESIEA signale dans son cours de Topologie, l'existence de quasi, pseudo et pré-topologie invitant les élèves à s'y intéresser dans leur projet. Pour stimuler la recherche et la démonstration mathématique, les seules informations qu'il donnera sur la pré-topologie est « d'enlever le quatrième axiome des voisinages topologiques » sans dévoiler les travaux de Marcel Brissaud et Gérard Duru.
Dans son projet Patrick Saint-Jean développera une systématique de la démonstration à partir de la Théorie des Catégories et démontrera les prévoisinages à partir des travaux de N. Bourbaki et ceux de Lipschutz, qu'il fera évoluer en 73 pour des besoins de topologie de réseau à destruction partielle avec les processus markoviens prétopologiques, puis en 74 au CEMAMu-CNET avec les textures de quanta sonores et de textures prétopologiques incorporable dans l'UPIC qu'il a conçu en 1975 pour Iannis Xenakis, et dès 74 au CEA avec les textures prétopologiques d'image en microscopie quantitative. Alors qu'il a déjà mis en place les Texturologies Quantiques Prétopologiques (1982), en 2004, il s'aperçoit que ses travaux initiaux son proche de Gérard Duru, mais les relations se mettront en place qu'avec Michel Terrenoire et Michel Lamure (dans un seul sens) puis dans les deux avec Hubert Emptoz qui sera rapporteur de sa thèse en 1989. Ce n'est qu'en 2010 qu'il rejoindra l'association Pretopologics où il découvre une floraison de chercheurs sur les systèmes complexes, mais qui sont restés dans la catégorie topologique à relation par foncteur transitif.
Avec
un
peu d'humour, à
l'instar de Leibniz
qui écrit à 18 ans en 1666, "De
l'art combinatoire",
point de départ d'une réforme profonde de la logique et
d'importantes recherches en mathématiques, Patrick
Saint-Jean
écrit un calcul trois siècles après, en 1967 à 18 ans qui annonce peut
être celui
"De
l'art trans-combinatoire". Humour
caractérisé par le fait qu'en art,
passer de la triologie à la tétralogie rajoute aux trois tragédies
celui du drame satyrique. Ce qui est le cas de la combinatoire comme
représentation du triangle dans la n-ième dimension (triangle de
Pascal) alors que la trans-combinatoire est la representation du cube
dans la n-ième dimension. On remarquera que la variété
trans-combinatoire est beaucoup plus grande que la variété
combinatoire. Elle introduit le point de vue local et la combinaison
d'éléments de propriétés différentes ou la relation d'adjacence n'est
pas transitive.
D'où toute
son
importance dans les jeux et les finances spéculatoires, mais aussi dans
le besoin de résoudre des problèmes d'ordre humain et sociologique où
la philosophie de la relation et de la différence du construire
ensemble prend toute son importance dans l'analyse et la démocratie
participative, un peu comme l'apport de l'urbanisme à l'architecture.
Pour information détaillée sur les travaux initiaux résultats des années 70-80, voici les publications en anglais,
TQPMAMUPHI/PretopologicalTheoryPSt-Jean.html
TQPMAMUPHI/PretopologicalTextureModelPSt-Jean.html
ainsi que le mémoire d'ingénieur ESIEA 1977, et le mémoire de thèse de doctorat 1989 de l'Université de Paris XIII.
TQPMAMUPHI/MemoireESIEA1977PatrickSaint-Jean.html
TQPMAMUPHI/TheseParis13GBM1989PatrickSaint-Jean.html
Transitif, pas transitif, non transitif, anti-transitif, intransitif ?
La question est posée posant tant des problèmes d’anglicisme que de mathématique.
En théorie des ensembles, un ensemble transitif est un ensemble dont tous les éléments sont aussi des parties de l'ensemble.
Un ensemble X est dit transitif si
- tout élément y d’un élément x de X est lui-même élément de X
c'est-à-dire si tout élément x de X est un sous-ensemble de X (en notant « ⊂ » l'inclusion au sens large) :
- ∀ x (x ∈ X ⇒ x ⊂ X)
ce qui revient à (en notant ∪X la réunion des éléments de X) :
- ∪X ⊂ X.
On parle également de classe transitive, avec la même définition : tout ensemble élément de la classe est également une partie de celle-ci.
L'ensemble vide et le singleton {∅} sont des exemples d'ensembles transitifs. Par contre le singleton {1} (où 1 = {∅}) n'est pas transitif :
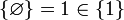 mais
mais
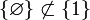 (car
(car
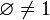 ).
).
Ordinaux
Les entiers de von Neumann sont des ensembles transitifs :
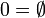 ,
,
 ,
, 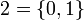 ,
, 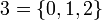 ,
, 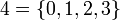 , … ,
, … , , ...
, ...
Par
exemple, pour
l’ordinal ![]() on a
on a ![]() et
et ![]() .
En effet
.
En effet ![]() et
et ![]() .
.
De façon plus générale les ordinaux de von Neumann, dont les entiers précédents sont les premiers éléments, sont aussi des ensembles transitifs. On peut d'ailleurs les définir comme les ensembles transitifs sur laquelle l'appartenance définit une relation d'ordre strict dont l'ordre large associé est un bon ordre. La classe de tous les ordinaux est une classe transitive : les éléments d'un ordinal sont des ordinaux.
Par transitivité l'appartenance entre deux ordinaux entraîne l'inclusion. On démontre que la relation d'inclusion sur les ordinaux est en fait la relation d'ordre large associée à l'appartenance (« appartient ou égal »).
Clôture transitive
On montre dans la théorie des ensembles de Zermelo-Fraenkel (ZF), que pour tout ensemble X, il existe un unique ensemble transitif Y contenant X et contenu dans tout ensemble transitif contenant X. On l'appelle clôture transitive de X. La clôture transitive est définie par récurrence sur les entiers naturels, représentés par les entiers de von Neumann dans le cadre ensembliste (on note ∪A la réunion des éléments de A, et ω l'ensemble des entiers de von Neumann) :
- Y0=X ; Yn+1=∪Yn ; Y = ∪n ∈ ωYn
Cette définition utilise le schéma d'axiomes de remplacement (pour que la suite des Yn soit bien une fonction, au sens ensembliste, définie sur ω).
-
L'ensemble Y est bien transitif : si x ∈ Y, alors pour un certain entier n, x ∈ Yn, et donc, par construction de Yn+1, x ⊂ Yn+1.
-
Par récurrence sur l'entier n, tout ensemble transitif contenant X contient Yn.
The transitive
closure
of a binary
relation R
on a set
X
is the transitive
relation R+
on set
X
such that R+
contains R
and R+
is minimal (Lidl and Pilz 1998:337).
If the binary relation itself is transitive,
then the transitive closure is that same binary relation; otherwise,
the transitive closure is a different relation.
For example, if X
is a set of airports and x
R y
means "there is a direct flight from airport x
to airport y",
then the transitive closure of R
on X
is the relation R+:
"it is possible to fly from x
to y
in one or more flights."
La fermeture transitive est une opération mathématique pouvant être appliquée sur des ensembles.
La
fermeture
transitive d'une relation
binaire ![]() sur un ensemble
sur un ensemble ![]() est la plus petite relation
transitive
est la plus petite relation
transitive ![]() sur
sur ![]() contenant
contenant ![]() 1.
1.
Si la relation ![]() est transitive,
alors on a l'égalité
est transitive,
alors on a l'égalité ![]() .
.
Sinon,
la fermeture transitive est définie comme :
Ce qui peut également se traduire ainsi :
La fermeture
transitive ![]() d'un graphe
d'un graphe
![]() est un graphe tel qu'il existe un arc entre toute paire de sommets
entre lesquels il existe un chemin. Ceci s'exprime également
ainsi :
est un graphe tel qu'il existe un arc entre toute paire de sommets
entre lesquels il existe un chemin. Ceci s'exprime également
ainsi :
A
transitive reduction of a binary
relation R
on a set
X
is a minimal relation
![]() on X
such that the transitive
closure of
on X
such that the transitive
closure of ![]() is the same as the transitive closure of R.
If the transitive closure of R
is antisymmetric
and finite,
then
is the same as the transitive closure of R.
If the transitive closure of R
is antisymmetric
and finite,
then ![]() is unique. However, neither existence nor uniqueness of transitive
reductions is guaranteed in general.
is unique. However, neither existence nor uniqueness of transitive
reductions is guaranteed in general.
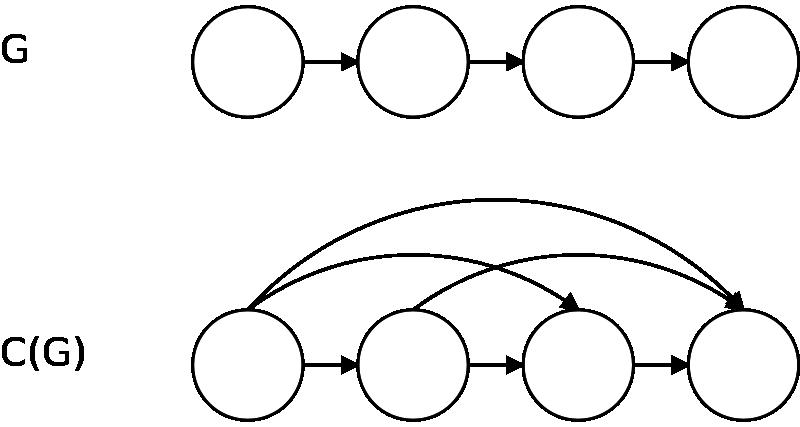
In graph theory, any binary relation R on a set X may be thought of as a directed graph (V, A), where V = X is the vertex set and A = R is the set of arcs of the graph. The transitive reduction of a graph is sometimes referred to as its minimal representation. The following image displays drawings of graphs corresponding to a non-transitive binary relation (on the left) and its transitive reduction (on the right).
The transitive reduction of a finite directed acyclic graph is unique.
The transitive reduction of a finite partially ordered set is its covering relation, which is given visual expression by means of a Hasse diagram.
The
transitive reduction ![]() of an acyclic relation
of an acyclic relation ![]() can be computed using its transitive closure
can be computed using its transitive closure ![]() :
:
La transitivité est une propriété éventuelle d'une relation binaire, mais non exclusive.
Une
relation binaire ![]() définie sur un ensemble
définie sur un ensemble ![]() est transitive
quand, à chaque fois que l'on a trois éléments x,
y
et z
de E
tels que x
et y
sont en relation, ainsi que y
et z,
alors x
et z
sont en relation. Plus formellement :
est transitive
quand, à chaque fois que l'on a trois éléments x,
y
et z
de E
tels que x
et y
sont en relation, ainsi que y
et z,
alors x
et z
sont en relation. Plus formellement :
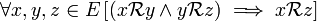 .
.
Si l'amitié était transitive, on pourrait affirmer « Tous les amis de mes amis sont mes amis.»
On en déduit qu'une relation sur E n'est pas transitive si et seulement s'il existe un triplet d'éléments de E qui fournit un contre-exemple à la transitivité : x et y sont en relation, ainsi que y et z, mais pas x et z. Plus formellement :
 .
.
On
dit alors que
la
relation binaire ![]() est non-transitive. Cette propriété, qui est la simple
négation de la transitivité, ne doit pas être confondue avec la
propriété suivante :
est non-transitive. Cette propriété, qui est la simple
négation de la transitivité, ne doit pas être confondue avec la
propriété suivante :
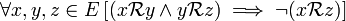 .
.
On dit parfois d'une telle relation qu'elle est anti-transitive (cette propriété est moins utile et moins courante que la transitivité, le vocabulaire n'est pas forcément bien établi).
Les propriétés de non-transitivité et d'anti-transitivité ne sont pas comparables : aucune des deux n'entraîne l'autre, en particulier une relation, même non vide, peut très bien être transitive et anti-transitive (il suffit qu'il n'y ait pas de triplet (x, y, z) vérifiant x R y et y R z).
Des exemples naturels montrent la variété de situations entre le transitif, le non transitif, l'anti-transitif et l'intransitif :
- Le voisin de mon voisin est mon voisin, mais pas toujours.
- L'ami de mon ami est mon ami, mais pas toujours.
- Le voisin de mon voisin n'est jamais mon voisin.
- L'ami de mon ami n'est jamais mon ami.
- L'ennemi de mon ennemi n'est pas forcément mon ennemi.
- L'ami
de mon ennemi n'est pas forcément mon ennemi.
- La différence de la différence n'est pas forcément la différence.
- L'indifférence de l'indifférence n'est pas forcément l'indifférence.
- Le ressemblance de la ressemblance n'est pas forcément la ressemblance.
- La relation "est le père de" est anti-transitive : si (a est le père de b) et (b est le père de c), alors (a n'est pas le père de c).
Une
relation de différence ![]() dans un ensemble
dans un ensemble ![]() est une relation
binaire
qui est à la fois réflexive, symétrique
et non transitive.
Ne pas confondre avec les relations de différenciation sur le
quantitatif. La différence est de nature qualitative.
est une relation
binaire
qui est à la fois réflexive, symétrique
et non transitive.
Ne pas confondre avec les relations de différenciation sur le
quantitatif. La différence est de nature qualitative.
Des dés non transitifs sont un ensemble de dés où, si un premier dé a plus de chances de donner un plus grand résultat qu'un deuxième et si celui-ci a plus de chance qu'un troisième, ce dernier peut tout de même avoir plus de chance de l'emporter sur le premier.
En d'autres termes, la relation « a une plus grande probabilité de donner un plus grand nombre » n'y est pas transitive.
Cette situation est similaire à celle du jeu pierre-feuille-ciseaux où chaque élément gagne par rapport à l'un des deux autres et perd par rapport au dernier.
Le phénomène de Rogers, attribué à Will Rogers, est un paradoxe qui fait monter la moyenne de deux ensembles lorsqu'on déplace un élément de l'un vers l'autre.
Le jeu de Tic tac toe est une jeu de transitivité non-transitivité.
Chez les anglophones :
-
A relation is intransitive if it is not transitive.
-
In freemasonry: it may be the case that lodge A recognizes lodge B, and lodge B recognizes lodge C, but lodge A does not recognize lodge C. Thus the recognition relation among Masonic lodges is intransitive.
Often the term intransitive is used to refer to the stronger property of antitransitivity.
We just saw that the feed on relation is not transitive, but it still contains some transitivity: for instance: humans feed on rabbits, rabbits feed on carrots, and humans also feed on carrots.
The term intransitivity is often used when speaking of scenarios in which a relation describes the relative preferences between pairs of options, and weighing several options produces a "loop" of preference:
-
A is preferred to B
-
B is preferred to C
-
C is preferred to A
Rock, paper, scissors is an example.
Assuming no option is preferred to itself i.e. the relation is irreflexive, a preference relation with a loop is not transitive. For if it is, each option in the loop is preferred to each option, including itself. This can be illustrated for this example of a loop among A, B, and C. Assume the relation is transitive. Then, since A is preferred to B and B is preferred to C, also A is preferred to C. But then, since C is preferred to A, also A is preferred to A. Therefore such a preference loop (or "cycle") is known as an intransitivity.
- Notice that a cycle is neither necessary nor sufficient for a binary relation to be not transitive. For example, an equivalence relation possesses cycles but is transitive. Now, consider the relation "is an enemy of" and suppose that the relation is symmetric and satisfies the condition that for any country, any enemy of an enemy of the country is not itself an enemy of the country. This is an example of an antitransitive relation that does not have any cycles. In particular, by virtue of being antitransitive the relation is not transitive.
- Analogously, in economics intransitivity can occur in a consumer's preferences. This may lead to consumer behaviour that does not conform to perfect economic rationality. In recent years, economists and philosophers have questioned whether violations of transitivity must necessarily lead to 'irrational behaviour' (see Anand (1993)).
- A BinaryRelation rel is intransitive only if (rel inst1 inst2) and (rel inst2 inst3) imply not (rel inst1 inst3), for all inst1, inst2, and inst3.
Quasitransitivity is a weakened version of transitivity that is used in social choice theory or microeconomics. Informally, a relation is quasitransitive if it is symmetric for some values and transitive elsewhere.
A binary relation T over a set X is quasitransitive if for all a, b, and c in X the following holds:
If the relation is also antisymmetric, T is transitive.
Alternately, for a relation T, define the asymmetric part P:
Then T is quasitransitive iff P is transitive.
Preferences are assumed to be quasitransitive (rather than transitive) in some economic contexts. The classic example is a person indifferent between 10 and 11 grams of sugar and indifferent between 11 and 12 grams of sugar, but who prefers 12 grams of sugar to 10.
Nous voyons donc qu'il existe une dualité entre le transitif et le non-transitif qui peut se réunir dans la transitivité partielle ou la non-transitivité partielle.
Faire vivre cette dualité, c'est accepter qu'il existe des morphismes et des foncteurs hétérogènes formant des précatégories et des prétopologies androgènes.
On dira que tout est question de voisinage, ou plutôt de prévoisinage homomorphique ou hétéromorphique voire andromorphique où le dosage est plus subtil et plus riche en variétés de structures et de fonctionalités.
Ces textures prétopologiques nous guiderons naturellement vers les texturologies quantiques prétopologiques pour les grandes collections finies et à structures dynamiques.
Voisinage et prévoisinage
Espace topologique et relation binaire transitive
Soit une topologie T sur un ensemble X définie à partir d'une famille V(x) de sous-ensembles de "voisinages de x", satisfaisant pour chaque élément x de X aux quatre axiomes suivants :
Toute partie de X contenant un élément de V(x) appartient à V(x) :

Toute intersection finie d'éléments de V(x) appartient à V(x) :
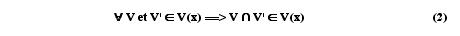
V(x) est non vide et x appartient à tous les éléments de V(x) :

Pour tout élément x de X et V1 de V(x), il existe un élément V2 de V(x) tel que pour tout élément y appartenant à cet autre élément V2 de V(x), le premier élément V1 de V(x) appartient aussi à V(y) :
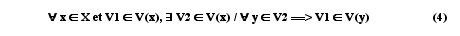
Alors V(x) est un système de voisinages de x, et (X,T) est un espace topologique défini sur X (Bourbaki 64, Lipschutz 65).
Soit,
dans ce même ensemble X, un sous-ensemble A(x), possédant x et une
relation binaire R dans X telle que :

THEOREME : Les propriétés de réflexivité et de transitivité de la relation binaire définissent un espace topologique sur un ensemble.
Les relations binaires ayant des propriétés de réflexivité et de transitivité, sont les relations d'équivalence et d'ordre, la propriété de symétrie et d'anti-symétrie les différenciant.
Espace prétopologique et relation binaire non transitive
Pour obtenir un espace prétopologique de l'espace topologique, il est nécessaire que les propriétés des éléments de l'ensemble X ne satisfassent pas à l'axiome (4) des voisinages.
THEOREME : Les propriétés de réflexivité et de non transitivité d'une relation ne définissent pas un espace topologique sur un ensemble mais un espace prétopologique.
Remarque : La non transitivité est soit l'intransitivité dans un espace à une dimension, soit une transitivité partielle dans les espaces de dimension supérieure.
En fait l'absence de l'axiome (4) est insuffisant pour définir les prévoisinages et il est préférable de définir un axiome de prévoisinage (4-bis), compatible avec la non transitivité de la relation binaire :
Pour tout élément x de X et V de V(x), il existe au moins un élément y de X, différent de x, et appartenant à V' de V(x) tel que V n'appartient pas à V(y) :
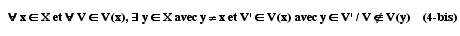
Cet axiome permet d'une part de construire un espace prétopologique sans passer par un espace topologique et d'autre part de différencier celui-ci des autres espaces prétopologiques construits à partir de propriétés différentes. Si nous percevons et décrivons un ensemble par l'aspect relationnel de ses éléments, il est restrictif et particulier d'utiliser uniquement des relations d'équivalence ou d'ordre nécessairement topologiques.
Espace de texture prétopologique et composition de relations
Une faculté de la perception est de comparer des espaces, des instants, des concepts, pour construire des sous-ensembles par rapport à leurs propriétés intrinsèques, et par rapport aux autres sous-ensembles ayant des propriétés intrinsèques différentes et qui du fait de ces différences engendre des configurations et des dispositions à l'intérieur de l'ensemble liés aux arrangements et liaisons des éléments et groupes d'éléments.
La composition mathématique de relations binaires donne pour résultat soit une relation transitive, si et seulement si toutes les relations composées sont des relations transitives, soit une relation non transitive, si et seulement si au moins une seule des relations composées est une relation non transitive.
Ainsi la composition des relations binaires nous permet de prendre en compte des frontières liées aux différences par les relations non transitives et des groupes liés aux similitudes par les relations transitives, et de créer des interférences entre des propriétés des deux genres, le résultat étant une relation non transitive définissant sur l'ensemble observé un ESPACE DE TEXTURE PRETOPOLOGIQUE, qui est un espace prétopologique.
L'existence d'interférences entre des propriétés définit pour nous la notion de TEXTURE.
Nous pouvons donc en différencier deux types :
-
la TEXTURE TOPOLOGIQUE dont les interférences sont créées entre relations transitives,
-
et la TEXTURE PRETOPOLOGIQUE dont les interférences sont créées entre relations transitives et non transitives. Les textures issues d'une seule relation sont dites dégénérées car non génériques d'interférences, par conséquent très limitatives dans la description de la texture.
Les textures topologiques créent des interférences disjointes donc pauvres. En effet les informations de texture topologique donnent une connaissance de type objet isolé et non de type relationnel comme les textures prétopologiques.
Méthodes de construction des espaces de texture prétopologique
Pour définir l'organisation structuro-fonctionnelle d'un ensemble, soit comme espace topologique, ou espace prétopologique, ou espace de texture prétopologique, plusieurs chemins peuvent être suivis suivant l'objectif et les moyens utilisés :
- L'état de fait : par connaissance, par vérification ou par définition, les éléments de l'ensemble possèdent les propriétés qui définissent l'organisation de l'ensemble.
- L'état d'observation statique : dans des conditions donnés, l'observateur perçoit des propriétés qui définissent l'organisation de l'ensemble. La délimitation des champs d'observation et des moyens de mesure quantitative ou qualitative, masque, inhibe, dévoile ou stimule les propriétés des éléments qui définissent le type d'espace de représentation.
- Le
processus
d'observation : l'observateur a des moyens d'action sur
l'environnement observé et sur son observation. L'observateur se
déplace dans l'environnement et dans les espaces mathématiques par
ajout ou retrait de propriétés selon l'existence ou non d'après
vérification ou simulation. Ici l'observateur peut donc faire varier
des degrés (résolution) ou des bornes (offset, gain) pour faire changer
la perception des éléments (plage de mesure, contraste et
différentiation optimisés) avec un controle visuel ou de façon
automatique algorithmique ou régulée
(mesure-analyse-traitement-synthèse-choix-action de réglage en boucle donnant
une série
convergente aux frontières irréductibles).
Espace
discret et ensemble des paramètres
Soit une banque de données, fournie par l'observation d'un système complexe, et représentée par un ensemble X de N éléments xi, points de l'image d'une entité réelle ou abstraite perçue et placée dans l'espace d'informations :
X = { xi / i = { 1,...,N } }
Les points d'une telle image ont des propriétés quantitatives ou qualitatives. Un type de propriété constitue un paramètre de l'image. La propriété elle-même quantifiée donne la valeur de la mesure ou, si elle est numérotée, la valeur du paramètre.
Les paramètres sont indicés suivant les entiers naturels :
J = { 1,2,...,n }, où n est le nombre total de paramètres.
Par exemple, ces paramètres sont temporels (instant, durée) ou spatiaux (lieux, coordonnées, distances, zones, etc.) ou qualitatifs quantifiés (fonctions, critères morphologiques, critères subjectifs, impressions, etc.). Soit un point muni d'une propriété, noté xij. Un point de l'image muni de l'ensemble de ses propriétés est un ensemble de points paramétrés :
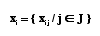
Un système informatique est capable de mesurer ou de calculer, sur l'image "mentale" de l'environnement réel observé, un ensemble I de paramètres indicés par J. Dans cet ensemble I, il est possible de définir des sous-ensembles I' de paramètres mis en jeu par le système sur une image donnée.
Remarque : le point image xi est une entité virtuelle ; sa représentation ne peut se faire que par la visualisation du point muni de ses propriétés xij, j appartenant à I'.
Relations entre les paramètres :
Soient sur l'ensemble de points paramétrés de l'image, des relations binaires réflexives séparables en deux groupes par leur propriété de transitivité et de non transitivité.
La relation transitive positionne de façon générale les éléments xij de X en relation avec un élément xkj donné quand ce dernier parcourt X :
xij R1 xkj <==> xij et xkj ont une propriété équivalente j
xij R2 xkj <==> xij et xkj ont une propriété ordonnée de type j
La propriété de transitivité donne une PERCEPTION GLOBALE de la relation entre les éléments de l'ensemble X. En effet xij en relation avec xkj peut être n'importe quel élément de X. La relation concerne le même type de propriété j pour les deux éléments. C'est une mesure relationnelle absolue car elle positionne des points par rapport à chaque autre point pris pour référence absolue pour lui donner une propriété. C'est donc une relation d'état.
La relation non transitive positionne de façon particulière les éléments xab de X par rapport à un élément xcd parcourant X.
xab R3 xcd <==> xcd inclut xab dans sa propriété d quelque soit b
Par exemple, dans ce cas, la propriété d des xcd est d'être associés à des xab, quel que soit leur propriété b, pour former un entourage, une zone, une distance, une structure ou une fonction.
La propriété de non transitivité donne une PERCEPTION LOCALE de la relation entre les éléments de l'ensemble X. En effet xab en relation avec xcd lui est associé pour donner la propriété d.
C'est une mesure relationnelle relative. Elle positionne un point de X avec chaque autre point pris pour référence relative en lui donnant une propriété. C'est une relation de transition d'états.
Texture par interférences relationnelles
Les relations forment des partitions telles que :
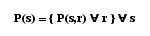
Ainsi les éléments de la partition P(s) pour le type de propriété s (ou paramètre) sont les sous-ensembles P(s,r) de X des éléments xi prenant la propriété r (valeur du paramètre).
La composition de deux relations (par exemple R1 et R3) forme des sous ensembles W((s,r),(t,u)) de X, qui possèdent les deux propriétés :
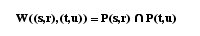
et constituent la famille des éléments de texture :

Pour comparer les éléments de texture, une distance exprime la différence entre deux éléments comme suit :

Les éléments de texture étant comparable, la séparation en sous-ensembles est créée par une frontière définie par la distance : les éléments dont la distance est inférieure ou égale à un, font partie d'un même ensemble. Les sous-ensembles créés ont des éléments possédant soit une relation commune (transitive ou non transitive) soit les deux et caractérisent par conséquent l'interférence relationnelle.
Chaque sous-ensembles correspond à une boule centrée sur un élément de texture et de rayon unitaire :
B(W((s,r),(t,u)),1)
Texture prétopologique par interférences relationnelles
Pour chaque élément de texture, définissons une famille de sous-ensembles par :
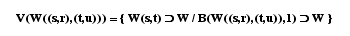
Cette famille V(W((s,r),(t,u))) valide les quatre axiomes définissant une prétopologie sur l'ensemble des éléments de texture.
V(W((s,r),(t,u))) est donc un système de prévoisinages de W((s,r),(t,u)) et donne à l'ensemble W(s,t) une structure d'espace prétopologique (W(s,t),P). Cet ensemble W(s,t) étant l'ensemble des éléments de texture par interférences relationnelles, (W(s,t),P) est un espace de texture prétopologique.
Descripteurs de texture prétopologique
Dans un espace de texture prétopologique, qui est un espace prétopologique, il est possible de définir le même type d'ensembles particuliers que pour les espaces topologiques.
Soit A un sous-ensemble de X. Le nombre d'éléments de A est son cardinal. L'ensemble X représente un ensemble W(s,t) d'éléments de texture. Donc x est un élément W((s,r),(t,u)) et y un élément W((s,v),(t,w)). Le sous-ensemble A de X représente un des sous-ensembles Ai de W(s,t). Dans les exemples, les sous-ensembles Ai sont définis par la relation transitive du fait de ses propriétés (mesure absolue, perception globale à fonction intégrante).
Un élément x de X est dit adhérent selon P à A inclus dans X, si il existe un sous ensemble W appartenant à V(x) tel que son intersection avec A soit non vide. L'ensemble des éléments adhérents à A selon P s'appelle Adhérence de A selon P, notée :
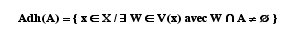
Le nombre d'éléments de Adh(A) est le cardinal d'Adhérence.
Un élément x de X est dit intérieur selon P à A inclus dans X, si il existe un sous ensemble W appartenant à V(x) qui soit inclus dans A. L'ensemble des éléments intérieurs à A selon P s'appelle Intérieur de A selon P, notée :
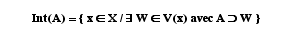
Le nombre d'éléments de Int(A) est le cardinal d'Intérieur.
D'autres ensembles particuliers marquent leur différence : l'extérieure Ext(A) de A est l'intérieur du complément de A par rapport à X ; la frontière F(A) de A, éléments de l'adhérence de A n'appartenant pas à son intérieur se décompose en deux semi-frontières, intérieure SFI(A) et extérieure SFE(A), suivant que les éléments respectifs appartiennent à A ou au complément de A par rapport à X. Mais trois ensembles particuliers, pour chaque sous-ensemble A, suffisent à décrire la texture de l'ensemble, les autres étant déductibles.
Nous retrouvons les mêmes définitions que les ensembles particuliers topologiques, mais avec une différence fondamentale liée à la prétopologie :

Ainsi
l'idempotence n'est pas toujours vraie --> Prétopologie et Texture
Prétopologique
Ces trois familles de cardinaux constituent les descripteurs élémentaires de la texture. Pour obtenir des descripteurs relatifs de la texture, il est possible d'établir des rapports pour chaque sous-ensembles particulier dont celui d'intérieur Ri(Ai) et d'adhérence Ra(Ai) en divisant respectivement les cardinaux d'intérieur et d'adhérence de chaque sous-ensemble Ai par leur cardinal respectif. La description de la texture relative a pour composantes deux rapports prétopologiques et le cardinal pour chaque sous-ensemble, les autres rapports étant déductibles.
Représentation de l'évolution de textures prétopologiques
Il est possible de construire des ECHELLES DE TEXTURES où chaque analyse de texture représente un DEGRE DE TEXTURE. Les relations binaires non transitives s'y prêtent en raison du type de propriété qu'elles confèrent à un élément en fonction d'un autre. Une relation d'ordre peut classer simplement ces degrés de texture. Mais l'échelle de texture peut être un système complexe organisé (chemin de description, discours, texture). La représentation suivant un ordre des degrés de texture est l'EVOLUTION DE TEXTURES.
Pour chaque espace de texture prétopologique, prenons le triplet des cardinaux (ensemble, intérieur, adhérence) pour tout sous-ensemble d'éléments de texture. Le cardinal du sous-ensemble caractérise son importance absolue en tant qu'objet. Le rapport de ce cardinal sur celui de l'ensemble total caractérise son importance relative en tant qu'objet dans son environnement. Le cardinal de l'intérieur du sous-ensemble caractérise son état d'isolement en tant que partie isolée de l'objet. Le rapport d'intérieur caractérise l'AGREGATION des éléments formant la partie isolée de l'objet par rapport à lui-même. Le cardinal d'adhérence caractérise son état relationnel en tant qu'objet étendu à tous les éléments de l'environnement et de lui-même qui sont en relation avec lui. Le rapport d'adhérence caractérise la DISPERSION de son environnement par rapport à lui-même.

Figure
1
Représentation à deux dimensions de l'évolution de textures

On remarque que l'espace de Topologie transitive ne représente qu'un point (RInt=1, RAdh=1) de l'espace des prétopologies non-transitives. La Topologie transitive est donc un cas limite de la prétopologie non-transitive.
Textures
prétopologiques dans l'espace des nombres complexes
S'il
est possible de compter le
cardianl des
ensembles particuliers où d'en connaître leurs rapports, il est aussi
intéressant d'effectuer des calculs plus complexes pour mesurer et
mesurer d'autres paramètres.
La
représentation
dans l'espace des nombres complexes décrit totalement la texture
en montrant les relations entre les sous-ensembles particuliers
prétopologiques d'intérieur (Int), de semi-frontière intérieure
(Sfi) et de semi-frontière extérieure (Sfe), d'adhérence (Adh),
d'extérieure (Ext),
les sous-ensembles (Ai) et l'ensemble (X) englobant amis
pouvant être lui-même que l'intérieur d'un sous-ensemble particulier
parmi d'autres, d'un ensemble qui le contient.
La texture prétopologique est définie par 6n+1 vecteurs complexes pour n sous-ensembles de l'ensemble X tels que :
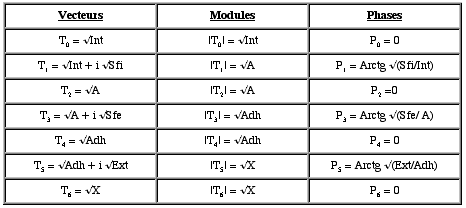
Les vecteurs T2, T4, T6 ont la même propriété que T0 d'être des vecteurs réels. Et par conséquent, il est possible de considérer les sous-ensembles particuliers prétopologiques A, Adh(A) et X, comme l'intérieur de sous-ensembles participant à une texture dans d'autres ensembles organisés.
Si la semi-frontière extérieure est plus petite que la semi-frontière intérieure, le sous-ensemble A est généralement concave (en boule ou renflements) dans son environnement.
Si la semi-frontière extérieure est plus grande que la semi-frontière intérieure, le sous-ensemble A est généralement convexe (en creux) dans son environnement.
Si la semi-frontière extérieure est sensiblement égale à la semi-frontière intérieure, le sous-ensemble A est généralement très filaire long et épais ou très carré dans son environnement.
Les mesures de l'agrégation et de la dispersion sont proportionnelles respectivement au carré des modules des vecteurs T0 et T3 ou T4.
Il existe d'autres propriétés remarquables à noter :
- quand les phases P1, P3 et P5 ont même valeur.
- quand l'extérieure est égale à la semi-frontière extérieure.
- quand l'extérieure est égale à la semi-frontière extérieure et la semi-frontière intérieure.
Quand les vecteurs complexes T1, T3 et T5 ont une phase non nulle, il exprime un facteur de pondération sur leur module pour en diminuer leur importance (histogramme des cardinaux des sous-ensembles). Ainsi, si l'histogramme joue un rôle important dans la description topologique d'un ensemble, et de sa texture (histogramme local), on remarquera que la texture prétopologique pondère celui-ci en fonction de l'environnement des sous-ensembles et des propriétés qui les organisent en texture de l'ensemble.

Figure 2
Représentation de la texture prétopologique
dans l'ensemble des nombres complexes.
En divisant les racines carrées par la racine du cardinal des sous-ensembles, on obtient l'équivalent d' amplitudes de probabilité de distribution qui définissent des « fonctions d'onde » particulières fondant la Théorie des Texturologies Quantiques Prétopologiques.
Pour des ensembles finis plus petits, le triplet pythagoricien nous donne les positions texturologies quantiques.
Un triplet pythagoricien est un triplet d'entiers naturels non nuls (x; y; z) vérifiant la relation de Pythagore : x2 + y2 = z2.

Analyse, traitement, simulation et synthèse prétopologiques
Pour un système X composé de n sous-systèmes, le nombre total de paramètres de texture devient important. Les méthodes classiques de classification sont alors compliquées, prennent beaucoup de mémoire et de temps calcul. Le concept d'image multiparamétrique, stockée en mémoire image des ordinateurs, est introduit pour définir une représentation visuelle de la banque de données facilitant une méthode de classification multiparamétrique et multihiérarchique et une description automatique ou très interactive. La classification initiale est prétopologique, mais selon les propriétés du système ou les objectifs de l'observateur, une ou plusieurs topologies peuvent être mis en évidence (Saint-Jean 86, 87, 89).
Quand la texture systémique n'est pas homogène, l'étude de la répartition des sous-systèmes à isotexture est nécessaire. La classification multihiérarchique fournit des groupes d'isotexture. La visualisation de la répartition montre une texture des sous-systèmes à isotexture qui peut être analysée par les mêmes méthodes.
L'observation d'un système et son fonctionnement peuvent être considérés comme en psychophysiologique de la vision (Molnar 85) : le mouvement des yeux (ou des informations) est guidé par la perception de la texture (ou la texture elle-même). Il existe des états (ou zones) entre lesquels l'oeil (l'information) effectue des saccades (mouvements) avec une probabilité de transition calculable et identifiable à un processus markovien : A * Pi = Pi+1.
Le processus markovien classique, partant d'un vecteur quelconque initial (observation locale), convergent vers un vecteur d'équilibre représentant le pourcentage des classes de l'histogramme (observation globale). Les transitoires caractérisent le système dans le cas d'un processus linéaire. Mais le vecteur d'équilibre n'apporte pas plus d'information que l'histogramme. Par contre, dans des processus prétopologiques markoviens, où les sous-systèmes sont les intérieurs, les semi-frontières intérieures et extérieures, les vecteurs de transition montrent des non linéarités et le vecteur de convergence est différent de l'histogramme. L'interprétation est spécifique à chaque sous-système considéré.
Trois types de simulation sont réalisés :
- processus entre intérieurs et semi-frontières intérieurs : pour passer de l'intérieur d'un système à celui d'un autre, il est nécessaire de passer par la semi-frontière intérieure, du premier, en relation avec les semi-frontières intérieures des autres. Ainsi, chaque sous-système est considéré, non pas comme topologiquement uniforme où chaque élément a des échanges symétriques avec les autres éléments lui appartenant ou pas, mais comme une structure plus complexe où les relations ne sont pas nécessairement symétriques, les intérieurs et semi-frontières intérieures de chaque ensemble pouvant variés suivant le degré prétopologique.
- processus entre semi-frontières intérieures et extérieures : les échanges concernent les propriétés ou les actions en bordure intérieure des sous-systèmes (relation de type membranaire).
- processus entre intérieurs, semi-frontières intérieures et extérieures : les échanges s'effectuent entre l'intérieur et la semi-frontière intérieure de chaque ensemble puis par l'intermédiaire des semi-frontières intérieures en relation. L'agrégation et la dispersion interviennent simultanément.
Les processus prétopologiques markoviens sont donc importants pour la simulation de l'observation et du fonctionnement des systèmes.
Le traitement (organisation active structuro-fonctionnelle) réalisé avant l'analyse est appelé prétraitement. Mais dans les processus bouclés, le traitement peut être à la fois l'action suivant une analyse et précédant une autre analyse. La synthèse peut être le résultat d'une pure construction, mais également celui de traitements successifs et variés à partir d'un système initial (restructuration, réorganisations successives).
Plusieurs types de traitements de texture prétopologique sont réalisables :
- changement de texture locale suivant l'image multi- paramétrique des descripteurs absolus (filtrage prétopologique),
- transformation de textures prétopologiques par influence locale (érosion et la dilatation prétopologiques);
- l'équilibrage des textures par mise en jeu de règles soit antagonistes (lois du plus fort, du plus faible, des plus forts, des plus faibles) à stratégie unique (un seul contre tous) et multiple (les uns contre les autres), soit coopératrices.
Le traitement est plus rapide et plus efficace que celui effectué par les filtres numériques de type Laplacien ou convolution.
Des résultats satisfaisants ont été obtenus en biologie cellulaire, à partir de la texture prétopologique des images numérisées.
D'autres paramètres que ceux mesurant la texture prétopologique peuvent être également pris en compte dans les méthodes. Mais le modèle est suffisamment général pour être employées dans tout autre domaine de la systémique (Bode 49, Bertalanfy 73).
Moteur sémantique du PolyAgogic CyberSpace
pour l'aide à la décision et la structuration dynamique des espaces interactifs de connaissances,
par les texturologies quantiques dans les espaces de textures prétopologiques,
et le Design du concept multimédia
Partant des constatations suivantes :
- La tekhnè ou technè, du grec τέχνη, désigne le savoir-faire des métiers de l’artisanat ou de l’art, l’action efficace, chez les Grecs de l’Antiquité. Elle s’oppose chez Aristote à la praxis, qui est la sphère de l’action proprement dite. La praxis (nf, d'origine grecque), signifiant action sous-tendue par une idée vers un résultat pratique, désigne l'ensemble des activités humaines susceptibles de transformer les rapports sociaux et/ou de modifier le milieu naturel.
- On oppose traditionnellement la pratique à la théorie. Mais la pratique recèle un savoir spécifique, savoir d'action ou savoir en action qui se distingue de la théorie censée la fonder ou en rendre compte et qui tient plus du savoir sur l'action.
- Si le scientifique fait modèle de la Nature, l'artiste prend la Nature pour modèle.
- Refusant toutes ces oppositions qui n'ont plus de sens dans un espace interactif de connaissance et de création numérique, le Digital Design ou Design Numérique et Design du concept multimédia, dans ses démarches et méthodes, mettent en rétroaction systémique, l'artiste prenant modèle de la Nature, et le scientifique faisant modèle de la Nature, ainsi que la technè et la praxis, la théorie et la pratique.
- La topologie fournie des méthodes axées sur la transitivité des relations (classe d'équivalence et ordre) permettant des hiérarchisations et une optimisation réductioniste et rationaliste.
- La prétopologie « classique » fournit des méthodes axées sur la transitivité et gère mieux les frontières topologiques en caractérisant les intérieurs et les adhérences par des préfiltres permettant la non-idempotence adh(adh(A) ≠ de adh(A), et ainsi une optimisation réductioniste et rationaliste de systèmes complexes plus fine mais se cantonnant à des classes d'équivalence et d'ordre (hierarchies).
- La texture prétopologique fournit des méthodes axées sur la non transitivité (mais pas nécessairement l'intransitivité ni l'anti-transitivité) permettant la mise en réseau dynamique, en texture assurant une multihiérachie, et en texturologie permettant une optimisation relationnelle non pas réductionniste mais mettant en relation des systèmes complexes irréductibles.
- La
topologie augmentée par la texture prétopologique permet
le passage entre espaces topologiques en fonction de la complexité
et de l'irréductibilité et le degré d'acceptation de la perte
d'information.
Notons que si le terme prétopologie a tout son sens comme étant
pré-topologique dans le repère des espaces emboités T0 (espace
prétopologique), T1, T2, T3, T4, T5 (espace métrique), il serait
intéressant de voir si cette « hypertopologie » ne
s'applique pas à tous les espaces Ti.
Les espaces Ti
n'étant pas que "emboîtés", l'ensemble des espaces
constituent une texture d'espaces de topologie augmentée.
- Les
textures prétopologiques permettent un assemblage d'éléments
différents en relations non transitives.
- Les
texturologies prétopologiques
permettent l'évolution vers des états stables multihiérarchiques.
- Les
texturologies quantiques prétopologiques
permettent la structuration dynamiques d'une organisation complexe en
considérant non pas seulement les cardinaux et les ratio
prétopologiques (d'intérieur, d'adhérence etc.) mais les fonctions
d'onde d'éléments répartis, tenant compte du module et de la phase
des concepts dans leurs interrelations.
Ainsi
l'espace-temps relativiste (-c.t.i, x, y, z) devient un espace-temps
de Minkowsky de quaternion ( c.t, ( i.x, j.y, k.z )) ;
où c.t représente une quantité, le cardinal de l'intérieur d'un sous-ensemble, et ( i.x, j.y, k.z ) les sous-ensembles de semi-membrane intérieure, semi-membrane extérieure et d'extérieure.
Ensuite la racine carrée des valeurs de
cardinal et la normalisation aux sous-ensembles contenant, sont
utilisées pour obtenir
une amplitude de distribution
(rapports quantiques relatifs) et ainsi obtenir un
modèle de fonctions d'onde qui libère de la nécessité de
connaitre les cardinaux,
généralement mal connus au départ.
Dans le cadre de la théorie généralisée des texturologies quantiques prétopologiques, l'espace-temps relativiste est alors transformé en une texture de quanta espace-temps formant des réseaux de réseaux d'éléments informationnels.
Le
quaternion de Minkowsky pourrait être également un quaternion
hyperbolique, ne respectant pas l'associativité, mais formant un quasigroupe -
ensemble muni d'un loi de composition interne (un magma) pour
laquelle (loi comme une multiplication), il est possible de diviser,
à droite comme à gauche, le quotient à droite et le quotient à
gauche étant uniques -. Ce quasigroupe fini est un carré
latin.
Un
chaos structuré de sous-ensembles m de niveau n, contenus dans des
ensembles l de niveau n+1, est alors un système de systèmes de
quinternions
{(√intm,n, i√smim,n, j√smem,n, k√extm,n,√intl,n+1)n,l,m}
le tout normalisé à chaque niveau pour faire apparaître les fonctions d'onde texturologiques.

et
en donner une version HPC
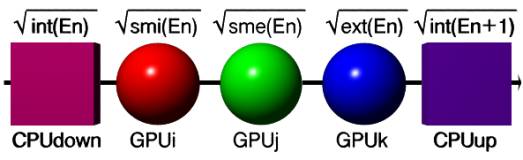
Si
l'on considère les niveaux d'ensemble comme des dimensions, il est
alors possible de définir une dimension supérieure à toute texture
de sous-ensemble.
En raison d'une part des
travaux appliqués en génie biologique et médical dès les années
70, et d'autre part la notion de texturologie qui sollicite des
interactions avec échanges, la notion de frontière mathématique
(ouverte ou fermée en topologie) est souvent remplacée par celle de
membrane (interactivités avec échanges permanents).
Au concept d'espace-temps (énergie de spin, énergie cinétique, énergie de rayonnement d'un univers à l'âge des ténèbres) s'adjoint ainsi un espace concept-relation (local-total-global où le concept est en fait le percept-concept-affect) ou ensemble-relation qu'il faut piloter paramétriquement afin de naviguer ou de survoler l'information conceptuel (zones structurées prétopologiquement) dans les espaces de connaissance interactifs, visualisables en immersion dans leur structures, leurs contenus et leurs déroulements explicatifs ou spectaculaires. Le concept de local-total-global prend donc toute sa signification. La texturologie locale des intérieurs des sous-ensembles est du type "rotation" (quaternion gauche de chaque sous-ensemble), une "énergie informationnelle de spin", plus complexe qu'en physique, donnant le sens contextuel et contexturel pragmatique. La texturologie totale est membranaire les liens assurant une "énergie cinétique" structurant ("colision" des concepts fondamentaux et pragmatique). La texturologie globale des intérieurs des ensembles distribués en sous-ensembles est du type énergie informationnelle rayonnante (émission de concepts fondamentaux) donnant le sens textuel et texturel polysémique d'un dictionnaire. Ainsi les "textons" (lemmes du lexique, phrase dans un paragraphe, paragraphe dans une page, page web dans un site ou ensemble de sites) se regroupent en "texturons" dans l'espace concept-relation.
Ainsi,
encore avec un peu d'humour : un siècle après
Albert Einstein et sa Théorie de la relativité,
Patrick Saint-Jean annonça sa Théorie des Texturologies Quantiques
Prétopologiques, à l'ESIEA en 2004 ( http://patrick.saintjean.free.fr/PACS/Bibliographie/TQ2004/TQ.html
), lieu de naissance de ces travaux sur les topologies et prétopologies
(1971), après sa conception de la Trans-combinatoire en 1967.
|
Et
dès 82, au Laboratoire de
Psychophysiologie de la perception
(François Molnar) en Arts Plastiques et Sciences de
l’Art de l’Université de Paris I, il montre par l’analyse de texture
appliquée aux mouvements des yeux (processus markovien et textures
prétopologiques) la possibilité d'identifier l'esthétique des oeuvres
d'art comme il identifie les textures cellulaires ou tissulaires et
leurs pathologies. Réalisation électronique d'un système d'analyse du
mouvement des yeux (lunette infrarouge et amplis opérationnels
asymétriques couplée à un oscillateur numérique Tecktronics et un
ITT2020, puis réalisation d'un logiciel d'imagerie sur le premier IBM
286, 16 millions de couleurs réalisé à base de cartes Matrox.
Espace de représentation dans l'espace complexe de Texture Quantique prétopologique (rapports quantiques) Analyse et Traitement d'image des textures prétopologiques (Années 80) |
Plusieurs
versions du
PolyAgogic CyberSpace voient le jour avec l'arrivée de l'Internet et
le développement des texturologies quantiques en intelligence
artificielle.
De l'UPIC au PolyAgogic CyberSpace :
Classification multi-hiérarchique multi-paramétriqueà partir de mesures de texture prétopologique (256).
Si le nombre d'images résultantes de la classification est 2 et est inversible, la classification est unique et topologique.
Si le nombre d'images résultantes de la classification est supérieur à 2, la classification est multihierarchique et prétopologique, et engendre un graphe.
Graphe 3D et moteur d'intelligence artificielle pour détecter des chemins optimum (en blanc)
servant de piste agogique pour la partition multi-piste.
Graphe dynamique 3D interactif et partition multipiste.
Présentation au Ministère de la Recherche rue Descartes pour les 50 ans de l'Intelligence artificielle en 2006
http://ru3.com/luc/tag/people/patrick-saint-jean-cybernetique-intelligence-artificielle.html

FractoCell 2D, fractale prétopologique 3-ième degré, © Patrick Saint-Jean, 1994.
FractoCell Rendu Ray-Tracing sur PoVRay, © Patrick Saint-Jean, 2007.
FractoCell 3D-Quaternion Unitaire et Texturologie Quantique, © Patrick Saint-Jean, 2010.



Ainsi numérisée, captée, analysée, structurée, abstraite, et virtualisée en temps réel à partir de la toile numérique, la connaissance remplit l'espace (knowledge mater). Puis visualisée sur plusieurs écrans, synthétisée, architecturée, texturée, elle est sculptée soit systémiquement par les texturologies quantiques et des moteurs d'intelligence, de conscience et de vie artificielles, soit interactivement dans une humanologie participative (intelligence collective à base d'intelligence personnelle, collaborative et coopérative), où les intervenants actifs et passifs créent ou inhibent les liens du réseau dynamique pondéré, travaillant ainsi la forme signifiante par effet de pleins et de vides colorés et ombragés. Scénarisée dans une mise en partition multi-piste, la sculpture, comme nouvelle écriture, se forme dans sa micro (quanta informationnel), mezzo (liens intimes entre percepts-concepts-affects matérialisés dans l'espace par des diodes laser montrant le polytope des points de vue) et macro composition (process temps réel) sculptant ainsi dynamiquement la matière de la connaissance et de l'ignorance.
Une nouvelle version HPC est élaborée par transformation du logiciel NBody d'Apple, pour visualiser des éléments du web (images jpg) à la place des étoiles, et intégrer les algorithmes de traitements, d'analyse et de classification multihiérarchique prétopologiques.
http://developer.apple.com/library/mac/#samplecode/opencl_nbody_simulation_example/Introduction/Intro.html
http://www.usm.uni-muenchen.de/people/puls/lessons/numpraktnew/nbody/nbody_manual.pdf
http://www.cs.cmu.edu/~scandal/alg/nbody.html
http://en.wikipedia.org/wiki/N-body_simulation
La réalisation HPC (high parallel computing) sur Mac Pro 12 cores et 2 cartes graphics Nvidia, 512 processeurs, permet la construction, la visualisation, le suivi, le contrôle, la manipulation interactive et la structuration automatique par moteur de texturologies quantiques prétopologiques, d'un graphe sémantique dynamique multimédia, temps réel de plus de 32000 concepts, à près de 140 Gigaflops/s et peut être étendu sur les Networks de type Cloud avec HPC.
Visualisation d'une base de données multimédia en grand nombre (8192).

Autostructuration de l'espace des concepts.
Mais ici se sont les forces physiques qui engendrent la texture prétopologique des masses différentes.
Les pages web sont alors caractérisées par une collection d'éléments ayant une "masse" mi soumis à une "gravité" G qui génère une "force de gravitation" élémentaire proportionnelle à la distance extérieure entre éléments et inversement proportionnelle au cube d'une pré-distance extérieure liée au paramètre de ramollissement et dont le cardinal est la mesure de la "force d'attraction" globale de chaque élément. Chaque "masse" est proportionnelle à une "masse propre" mais dépend d'un paramètre d'étendue, de distance intérieure, le "rayon" r dont elle est proportionnelle du carré et inversement proportionnelle au carré d'une pré-distance intérieure lié au paramètre d'atténuation favorisant l'agrégation.
L'ensemble des couples (atténuation, ramollissement) définit une famille de prévoisinages caractérisant l'espace prétopologique.
Espace de mesure et Classification Multiparamétrique Multihiéarchique
A partir de signatures prétopologiques, le système dynamique s'auto-structure
Cette réalisation est un hommage à Edouard Glissant, décédé en février 2011, Philosophe et poète de la Relation et de la Différence.
Mais également, en réflexion de la définition logico-mathématique de l'auteur, c'est aussi en hommage premier dès 1982 à Jean Dubuffet (1901-85) qui, associant à ses peintures les projections à d'autres moyens pour obtenir des nappes finement ouvragées donnant "une impression de matière fourmillante, vivante et scintillante, évoquant toutes espèces de textures indéterminées voire des galaxies ou des nébuleuses", auxquelles il donna le nom de Texturologies pour les différencier des Topographies, et se muer en Empreintes résillées dont l'idée tient à ceci que "les points qui semblaient autant de piqûres, se mettent à remuer, à filer, à faire voir en dessous d'eux-mêmes tout un réseau".
Tout comme Iannis Xenakis dans ses Musiques formelles, Jean Dubuffet s'interroge sur ses textures continues et informes, qui investissent uniment la surface comme un gaz occupe un volume évoquant un phénomène physique d'entropie, liée à la perception relative de l'observateur d'un équilibre du désordre et de l'ordre. Et il en est de même quand, dans ses expériences musicales où il ressent "qu'il y entre en jeu mille choses subtiles, toutes liées entre elles il est vrai et difficiles à isoler, où participent le quantum de lustrage et les variations de textures", par rapport au quanta sonore de Xenakis comme un signal élémentaire de Gabor, et qui confirme ou converge avec les travaux de l'auteur sur la justification d'un modèle de texturologies quantiques prétopologiques, dans sa recherche de nouvelles écritures en contexte et contexture, depuis les années 60, où en Design le "kit-it yourself" (montez le vous-même) remplace le "do-it yourself" (faites le vous-même) et par contre coup provoquera la volonté d'un "live-it yourself" (vivez-le vous-même).
Edgard Morin, penseur de la complexité qu'il constate dans l'Esprit du temps (Névrose des années 60, puis Nécrose des années 70) définit sa méthode de connaissance pour traduire la complexité du réel et reconnaître l'existence des êtres et approcher le mystère des choses (La Nature de la Nature, La Vie de la Vie, La Connaissance de la Connaissance, L'Humanité de l'Humanité), qui le fera défier les classements disciplinaires pour tenter une réforme de la pensée.
Dans le sens d'Edgard Morin, Michel De Certeau, Voyeurs ou marcheurs, dans L'invention du quotidien, qui se questionne, en citant Manhattan vu du 110e étage du World Trade Center, sur « L'immense texturologie qu'on a sous les yeux est-elle autre chose qu'une représentation, un artefact optique ? C'est l'analogue du fac-similé que produisent, par une projection qui est une sorte de mise à distance, l'aménageur de l'espace, l'urbaniste ou le cartographe. La ville-panorama est un simulacre « théorique » (c'est-à-dire visuel), en somme un tableau, qui a pour condition de possibilité un oubli et une méconnaissance des pratiques. Le dieu voyeur que crée cette fiction et qui doit s'excepter de l'obscur entrelacs des conduites journalières et s'en faire l'étranger. »
et mettant ainsi en dialectique la texturologie qui lui serait topologique (relatif aux déformations de figures) et non topique (définisseur de lieu) selon donc une texturologie prétopologique de proximités successives liées à la texture dans son mouvement, en instaurant une diégèse, une narration, marche du guide qui passe à travers par transgression, regroupées par l'auteur comme une topologie augmentée dans une paradiégèse. "Là où la carte découpe, le récit traverse", mais où les narrateurs sont multiples, et où faire surfer sur le net (buzzer en créant la vague) devient une façon de "slamer" sur le net à plusieurs.
Pretopological Texture Marqued Language et Pretopological Quantics Texturology Marqued Language
Pour ce faire les pages web incluent un PTML (Pretopological Texture Marqued Language) ou métalangage comme l'IEML de Pierre Levy, qui ne soit pas Topologique mais Prétopologique et Texturologique, pour assurer l’interopérabilité sémantique, dans un contexte de mondialisation du mental (pas seulement la mémoire mais le percept-concept-affect du Mental Design, et pas seulement l'esprit mais le mental de la Society of the Mind où l'âme des peuples à encore quelque chose à dire et à vivre), et ainsi l'effort de gestion de la connaissance pour sa polyagogie, sa création et son spectacle (oeuvre, cours, conférences) dans des espaces d'immersion interactif.
Vers une Théorie des Précatégories
L'exercice
est de passer de la
combinatoire à
la transcombinatoire en tenant compte que la structure sera formée d'un
ensemble transcombiné à une ou plusieurs lois de compositions dont
l'une au moins est non-transitive.
A partir des Structures algébriques élémentaires
Une structure algébrique est un type particulier de structure. Sa spécificité par rapport aux autres types de structure est d'être formée d’un ensemble combiné à une ou plusieurs lois de composition, éventuellement complétées par un ordre ou une topologie, le tout satisfaisant un certain nombre d'axiomes.
Structures à opérateurs internes
Partant
d'un magma
(ou monade
ou groupoïde
de Ore1)
qui est une structure
algébrique
constituée d'un ensemble
muni d'une loi
de composition interne, le couple
noté ![]() . On appelle loi
de composition interne
sur un ensemble E
toute application
. On appelle loi
de composition interne
sur un ensemble E
toute application
![]() du produit
cartésien E
× E
dans E.
Dans un magma ( E,
du produit
cartésien E
× E
dans E.
Dans un magma ( E, ![]() ), on appelle « composé
d'un élément x
par un élément y »,
l'unique élément x
), on appelle « composé
d'un élément x
par un élément y »,
l'unique élément x ![]() y
associé par la loi
y
associé par la loi ![]() au couple ( x, y
). L'élément y
au couple ( x, y
). L'élément y ![]() x
est le composé de y
par x.
Il est associé par la loi
x
est le composé de y
par x.
Il est associé par la loi ![]() au couple ( y, x
), réciproque
du couple ( x, y
); c'est pourquoi il est aussi appelé composé
réciproque
de x
par y
ou de x
au couple ( y, x
), réciproque
du couple ( x, y
); c'est pourquoi il est aussi appelé composé
réciproque
de x
par y
ou de x ![]() y.
Un élément
y.
Un élément ![]() est dit idempotent
ou projecteur ssi :
est dit idempotent
ou projecteur ssi :
![]()
Soit E
un ensemble à n
éléments. Le nombre de lois internes sur E
est le nombre
d'applications de E×E
dans E,
soit ![]()
On peut compter de même combien, parmi elles, sont commutatives. Une loi commutative sur E est entièrement déterminée par sa valeur x✲y=y✲x pour les paires {x,y} et sa valeur x✲x pour les singletons {x}. Le nombre de ces paires et singletons étant
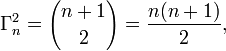
il
y a donc ![]() lois commutatives sur E.
lois commutatives sur E.
Le Monoïde est un magma associatif et unifère. Donc un magma fermé.
Structures à opérateurs externes
Algébriquement, une structure externe est un ensemble muni d’une loi de composition externe sur une structure de base, et éventuellement d’une ou plusieurs lois de composition interne. Géométriquement, c’est un ensemble E sur lequel agit un ensemble-opérateur S, encore appelé ensemble des opérateurs ou scalaires. Pour cela, l'ensemble E est muni d’une action, c’est-à-dire d’une application de S dans EE (ensemble des transformations de E, c'est-à-dire des applications de E dans E). La correspondance entre les actions et les lois externes est bijective; c’est pourquoi les lois externes sont souvent appelées lois d’action.
Moduloïdes : Structures possédant à la fois une loi de composition interne et une loi de composition externe. Le magma est alors ouvert.
Nous pouvons donc créer de nouvelles structures élémentaires :
Structures à opérateurs hétérogènes : les Morphoïdes différents des morphismes d'opérateurs homogènes.
Structures à opérateurs homogènes et hétérogènes : les Androïdes à homomorphismes et hétéromorphismes formant des textures et texturologies prétopologiques.
Remarques :
1 - Plus le temps passe (45 ans), plus les publications évoluent, se précisent et se confirment, plus les différences s'accroissent entre les travaux d'une part de la topologie de Bourbaki et de la prétopologie de Brissaud, et ceux d'autre part des textures prétopologiques et texturologies quantiques prétopologiques de Patrick Saint-Jean qui s'affirment ; et poussent ce dernier à croire qu'il est un non-mathématicien comme de nombreux esthéticiens sont non-esthéticiens et nombreux philosophes sont non-philosophes et qui, s'interrogeant sur la nature profonde de l'Etre dans un processus rétro-actif de Design, prennent la "Nature" pour modèle en tant qu'artiste, pour en faire des modèles de la Nature en tant que scientifique (bouclage temps réel de l'analyse et la synthèse dans un même processus mental). Heureusement l'écriture mathématique professorale actuelle rejoint l'écriture mathématique processorale (informatique), encore virtuelle mais qui arrive maintenant par l'informatique appliquée aux mathématiques (Mathematica de Wolfram et autres), et permettent de rendre compte d'une telle évolution dans l'union des différences subtiles.
En fait le modèle reste dans le langage mathématique et l'analyse passe par le qualitatif et le quantitatif, donc "l'observation et la mesure sensible" où l'observé et l'observant se côtoient en toute dépendance et où la continuité se traduit par des proximités successives engageant un "axiome de choix structuro-fonctionnel-systémique" à chaque étape.
Dans quelle structure l'élément se trouve-t-il dans son action ? Dans quelle structure l'élément se trouvera-t-il après son action ? Quelle situation, quelle condition stimule l'action ?
Tout semble reposer sur la propriété la plus simple :
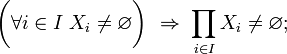
où si les Xi sont des classes d'équivalences en situation de proximité (regroupement des composantes principales dans une structure élémentaire (texton, texturon, texel), ils forment un complexe ayant une texture hétérogène de quantité mais pas de nature (texture topologique), alors que si les Xi sont des parties à propriétés relationnelles non-transitives entre éléments de natures différentes, ils forment un complexe ayant une texture hétérogène de nature (texture prétopologique).
L'introduction des texturologies quantiques prétopologiques relationnelles nous place dans un monde de systèmes de quinternions complexes (RC3R)n pour structurer un monde relationnel en osmose au monde relativiste physique.
2 - Mais ces différences se caractérisent par le besoin de relacher une propriété qui semble essentielle (pour ne pas dire culturelle) en Théorie des Catégories tout comme en Topologie, voire en Prétopologie au sens de Brissaud et des prétopologistes lyonnais, qui est la "transitivité" des relations permettant et assurant la classe d'équivalence et l'ordre total par la relation transitive d'équivalence et d'ordre (anti-symétrie).
En effet comment rompre avec une culture ancestrale où "le voisin de mon voisin est mon voisin", où "l'ami de mon ami est mon ami", ... enfin presque par pure idéologie ou besoin de faire confiance au risque de toutes les trahisons, et qui rappelle la Royauté de Droit Divin fait d'ordre et de classe et dont la transcendance de haut en bas est absolue.
C'est sans doute dû à la théorie des ensembles de von Neumann–Bernays–Gödel, abrégée en NBG ou théorie des classes, qui est une théorie axiomatique essentiellement équivalente à la théorie ZFC de Zermelo–Fraenkel avec axiome du choix (et avec les mêmes variantes possibles), "mais dont le pouvoir expressif est plus riche".
En mathématiques, la notion de classe généralise celle d'ensemble. Les deux termes sont parfois employés comme synonymes, mais la théorie des ensembles distingue ces deux notions. Un ensemble peut être vu comme une collection d'objets, mais aussi comme un objet mathématique, qui en particulier peut lui-même appartenir à un autre ensemble. Ce n'est pas forcément le cas d'une classe, qui est une collection d'objets que l'on peut définir, dont on peut donc parler, mais qui ne forme pas nécessairement un ensemble. Quand une classe n'est pas un ensemble, elle est appelée classe propre. Elle ne peut alors être élément d'une classe (ni, a fortiori, d'un ensemble). En théorie des ensembles, ces collections d’objets, qui sont définies par une propriété de leurs éléments, mais qui ne sont pas forcément des ensembles au sens de la théorie, sont appelées classes. Les classes qui ne sont pas des ensembles sont appelées classes propres. On peut voir celles-ci comme des collections que l’on peut décrire dans la théorie, mais qui sont trop « grosses » pour être des ensembles.
Mais
les classes
peuvent-elle être hétérogène ? Et les morphismes des
hétéromorphismes ?
Alors (avec humour) comment actuellement ne pas risquer de se
faire accuser d'homophobie en "dénonçant" "l'hégémonie" de
l'homomorphisme en voulant introduire un hétéromorphisme et un
andromorphisme ?
Par "habitus" la classe étant d'office d'équivalence,
il
est préférable de parler de "parties".
La "théorie des parties" obtient ainsi un pouvoir expressif
encore plus riche que la théorie des classes.
Peut on parler également de topologie trans-combinatoire comme on parlait de topologie combinatoire (ancien nom de la topologie algèbrique) ?
3 - Si la définition de la Topologie a progressé avec l'annonce des quasi, pseudo, pré-topologies dès les années 60 et 70, la normalisation converge vers le besoin et l'exigence de transitivité, et les notions de préfaisceaux, prébase, préfiltre, prévoisinage, de quasi-compact, relativement compact, localement compact, sigma-compact (axiomes de recouvrement) montrent la complexité inhérente et paradoxale tout en relachant les machoires de certains étaux d'une "inquisition" culturelle.
Ainsi la Topologie parait à la fois "une vision globale" de grande valeur, mais aussi une sorte de "bondieuserie" mathématique globalitaire où tout est parfait et totalement défini, fait de classes et d'ordre, à mettre d'une part en opposition aux "bourdieuseries" de la philosophie de l'action stratégique de l'habitus et de la violence symbolique de Pierre Bourdieu pour se détourner de l'habitus, et d'autre part à l'encontre de la pratique de la réalité concret-abstrait-virtuel exprimée par les idées sur la nature et la pensée complexe qui nécessitent de nouvelles écritures et d'une vision locale non isolée dans la globalité (1968, droit à la différence, à l'irréductibilité, à l'imaginaire, à l'indépendance et l'autodétermination ainsi qu'à l'autogestion d'une "société démocratique sans domination des ordres et des classes" ), fondées sur les interférences du local-global qui engendre la diversité de l'art total (Nicolas Schöffer) dans son expansion entropique du local-total-global autonome.
Mais
un pas reste à
faire ; pas en avant ?, pas en arrière ? peut importe, peut-être une
chorégraphie dans la continuité
culturelle et la proximité successive, à côté dans l'union des mondes
parallèles ensembles dont
le voisin n'est pas forcément mon voisin (et constater que l'ami de mon
ami n'est
pas forcément mon ami) où le droit à la différence et à l'union
des différences sont possibles.
Et si l'identité a l'habitude culturelle de faire l'union, et l'union
de faire la force, alors la différence peut faire également l'union et
l'union amalgamée faire une autre force. Et l'union des identités et
des différences dans la texture font le mouvement (texturologies).
Alors, là, le mathématicien devient-il philosophe, et le philosophe
engagé dans une aventure de sciences plus humaines, voire politique ?
La
question est
posée, mais d'abord cherchons les différences.
Les Précatégories non-transitives
A partir du moment où l'on accepte le foncteur oubli concernant la règle de transitivité absolue pour n'accorder à la structure qu'une possibilité d'être transitive ou intransitive, la possibilité d'être non-transitive répond à un plus grand nombre de cas.
Les morphismes ne sont plus que homomorphiques mais peuvent être hétéromorphiques voire andromorphiques (à la fois homo et hétéroromorphique).
Les catégories
deviennent des précatégories qui redeviennent des catégories quand les
hétéromorphismes n'exitent plus et que les andromorphismes sont devenus
homomorphiques.
Là peut se jouer
la propriété des foncteurs d'être covariants ou contravariants ou
mixtes.
Un foncteur (ou foncteur
covariant)  d'une catégorie
d'une catégorie 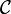 dans une
catégorie
dans une
catégorie 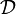 est la
donnée
est la
donnée
- d'une fonction qui, à tout
objet
 de
de  , associe
un objet
, associe
un objet  de
de  ,
, - d'une fonction qui, à tout
morphisme
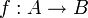 de
de  ,
associe
un morphisme
,
associe
un morphisme 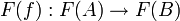 de
de  ,
,
qui
- respectent les
identités : pour tout objet
 de
de  ,
,
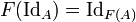 ,
,
- respectent la
composition : pour tous objets
 ,
, 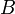 et
et 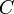 et
morphismes
et
morphismes 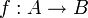 et
et 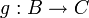 de
de 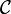 ,
,
 .
.
Un foncteur contravariant
G d'une
catégorie 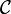 dans une
catégorie
dans une
catégorie 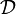 est un
foncteur covariant de la catégorie opposée
est un
foncteur covariant de la catégorie opposée 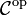 dans
dans 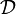 (à tout
morphisme
(à tout
morphisme 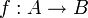 de
de 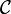 il
associe donc un morphisme
il
associe donc un morphisme 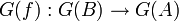 de
de  , et on a
la « relation de compatibilité »
, et on a
la « relation de compatibilité » 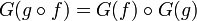 ).
).
On voit immédiatement que l'image
d'un isomorphisme
par un foncteur est un isomorphisme.
Un foncteur
 est
appelé une équivalence
de catégories (en)
s'il existe un foncteur
est
appelé une équivalence
de catégories (en)
s'il existe un foncteur 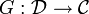 tel
qu'il existe un isomorphisme naturel de foncteurs
entre
tel
qu'il existe un isomorphisme naturel de foncteurs
entre 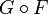 (resp.
(resp. 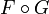 ) et
l'identité sur
) et
l'identité sur 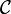 (resp.
(resp. 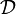 ). Une
équivalence de catégories est une notion plus générale que celle des
isomorphismes de catégories.
). Une
équivalence de catégories est une notion plus générale que celle des
isomorphismes de catégories.À partir d'une catégorie 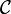 ,
on peut définir une autre catégorie
,
on peut définir une autre catégorie  (ou
(ou 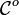 ),
dite opposée ou duale, en prenant les mêmes objets,
mais en inversant le sens des flèches.
),
dite opposée ou duale, en prenant les mêmes objets,
mais en inversant le sens des flèches.
Plus précisément : 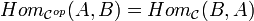 ,
et la composition de deux flèches opposées est l'opposée de leur
composition :
,
et la composition de deux flèches opposées est l'opposée de leur
composition :
Il est clair que la catégorie
duale de la catégorie duale
est la catégorie de départ : 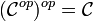 .
.
Cette dualisation extrêmement
simple permet de symétriser
la plupart des énoncés, ce qui peut être douloureux pour les
irréductibilités. Mais c'est un moyen dynamique de prendre conscience
et de se poser la question du possible, du faisable et d'évaluer
l'impact, afin de décider la réductibilité ou pas, gardant ainsi les
limites des frontières à ne pas franchir, des irrégularités texturelles
séparant les milieux et définissant les membranes.
Une flèche  est dite un monomorphisme lorsqu'elle vérifie la
propriété suivante : pour tout couple
est dite un monomorphisme lorsqu'elle vérifie la
propriété suivante : pour tout couple 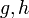 de flèches
de flèches 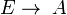 (et donc aussi pour tout
(et donc aussi pour tout 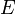 ),
si
),
si 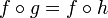 ,
alors
,
alors 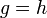 .
.
Une flèche  est dite un épimorphisme lorsqu'elle vérifie la
propriété suivante : pour tout couple
est dite un épimorphisme lorsqu'elle vérifie la
propriété suivante : pour tout couple 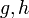 de flèches
de flèches 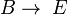 (et donc aussi pour tout
(et donc aussi pour tout 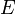 ),
si
),
si 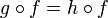 ,
alors
,
alors 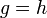 .
.
Les notions de monomorphisme et d'épimorphisme sont duales l'une de l'autre : une flèche est un monomorphisme si et seulement si elle est un épimorphisme dans la catégorie duale.
Une flèche  est dite un isomorphisme s'il existe une flèche
est dite un isomorphisme s'il existe une flèche 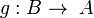 telle que
telle que 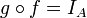 et
et 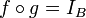 .
Cette notion est autoduale.
.
Cette notion est autoduale.
L'exercice
est
donc de remplacer les opérateurs Hom par ceux d'Heter et Andro en
découvrant et vérifiant la cohérence de leurs propriétés :
Une
NT-Précatégorie ![]() (non-transitive
précatégorie) est la donnée de
quatre éléments :
(non-transitive
précatégorie) est la donnée de
quatre éléments :
-
Une catégorie dont les éléments sont appelés objets ;
-
Un ensemble
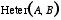 ,
pour chaque paire d'objets de
nature différente
,
pour chaque paire d'objets de
nature différente 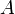 et
et 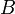 ,
dont les éléments
,
dont les éléments 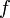 sont
appelés NTmorphismes (ou flèches) entre
sont
appelés NTmorphismes (ou flèches) entre 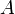 et
et 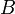 , notés
, notés  ;
;
-
Un NTmorphisme
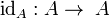 , pour chaque objet
, pour chaque objet 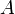 , appelé identité
sur
, appelé identité
sur 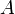 ;
;
-
Un NTmorphisme
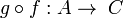 pour toute paire de
NTmorphismes
pour toute paire de
NTmorphismes  et , appelé composée de
et , appelé composée de 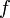 et
et  , tel que :
, tel que :
- la composition est associative : pour tous hétéromorphismes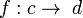 ,
, 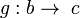 et
et 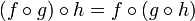
- les identités sont des éléments neutres de la composition : pour tout NTmorphisme ,
, 
On
demande aussi
que : si ![]() .
.
Cela
revient à
agréger ou à disperser les éléments de nature différente sans perdre le
fait qu'ils sont liés entre eux et qu'ils forment une texture
prétopologique.
Et
de les mettre
en jeu :
Dans un jeu de Tic-Tac-Toe l'ensemble est une grille de 3 par 3 composée de O et de x.
Dans un jeu de stratégie comme Risk, où les territoires se négocient entre amis et ennemis dans l'espace-temps.
Préfoncteur hétéromorphique
Produit et Somme Topologiques
Dans une catégorie, la somme peut s'exprimer par une propriété universelle ou de manière équivalente comme foncteur représentable.
Les préfoncteurs homomorphiques, hétéromorphiques ou andromorphiques sont donc représentables.
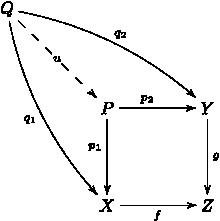
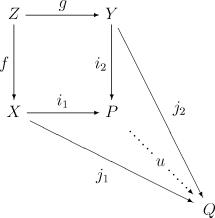
Pullback (produit fibré, somme topologique)
dual
du Pushout (somme amalgamée, quotient de l'union disjointe)
- X et Y sont de même nature (homomorphisme)
- X et Y sont de nature différente (hétémorphisme)
- X et Y peuvent être de nature différente ou de même nature (andromorphisme)
- Z est une texture homogène (homomorphisme, topologie identitaire), une texture hétérogène (hétéromorphisme, topologie dispersive), ou une texture androgène (andromorphisme, texture prétopologique).
Diagramme d'une I-catégorie


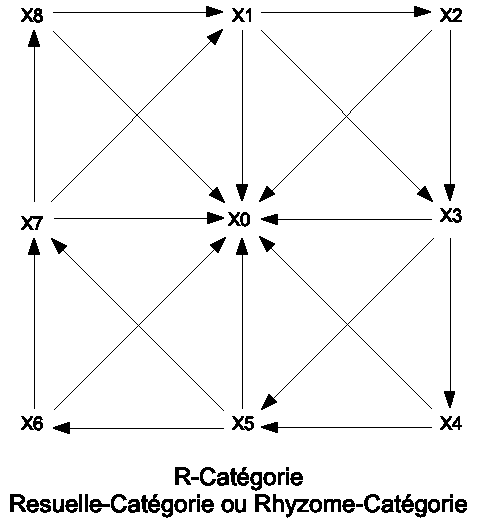
Résultats obtenus à l'aide de Wolfram Mathematica 8 :
Utilisant la théorie des graphes et les bibliothèques correspondantes, nous cherchons à modéliser notre problématique de texture prétopologique dans les précatégories.
En effet à partir du moment où les foncteurs peuvent être homo, hétéro ou andromorphiques, il nous faut considérer des relations transitives et non-transitives en même temps (graphe et diagramme à flèches uni-orientées ou orientées symétriquement ou orientées parallèlement).
Ainsi nous visualisons deux graphes de noeuds et arrêtes directionnelles en détectant le voisinage et montant l'appartenance des noeuds et arrêtes aux ensembles particuliers prétopologiques (liaisons intérieur en rouge, semi-frontière intérieure en vert, semi-frontière extérieure en bleu, extérieur en jaune, noeuds intérieur en magenta, semi-frontière intérieure en vert, semi-frontière extérieure en bleu, extérieur en jaune).
Premier sous-ensemble A (ou premier graphe1) : 5 noeuds et 10 liaisons
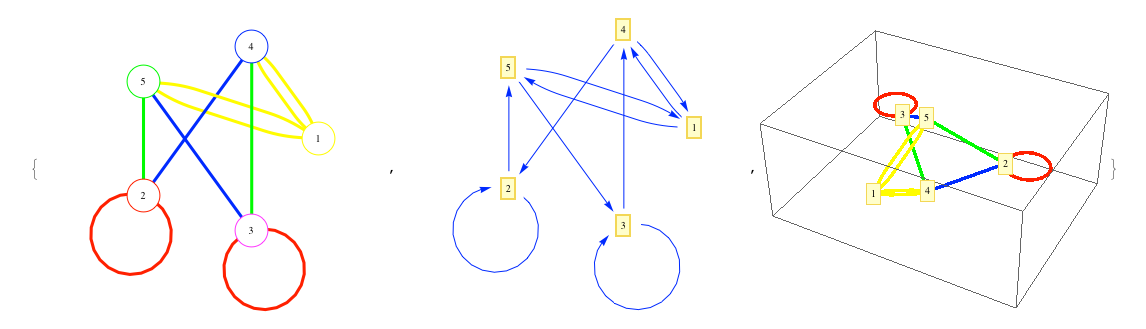
Deuxième sous-ensemble B (ou graphe2) : 5 noeuds et 10 liaisons

Et superposons les deux ensembles pour former un ensemble X (Graphe3= Graphe1 + Graphe2)

Pour que cet ensemble X soit un espace topologique, il nous faut chercher sans fermeture transitive.
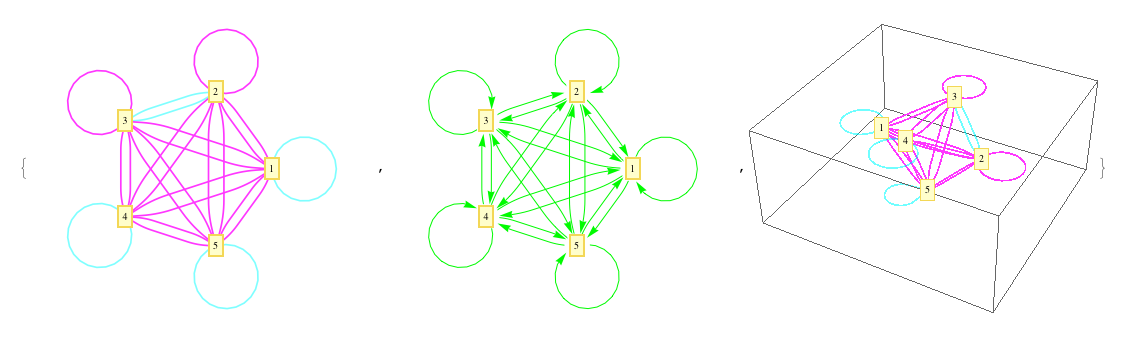
En fait cette fermeture transitive est un sous-ensemble de l'ensemble X qui a également ses propre sous-ensembles prétopologiques particuliers

Ainsi la fermeture transitive peut être une limite, un bord, une convergence topologique, mais, également dans la struture, un sous-ensemble comme les autres sous-ensembles qui forment une espace prétopologique.
Dans un graphe structurel voulant représenter les sous-ensembles d'un ensemble, lui même sous-ensemble d'un ensemble, etc et dont chaque intérieur possède des sous-ensembles, il est préférable de décomposer les noeuds intérieur, semi-frontière intérieure, semi-frontière extérieure, et extérieur en mini-chaine come le montre le schéma suivant.
Combinatoire et permutation de chaque noeud est possible pour une expression topologique.


Combinatoire,
triangle de pascal, triangle dans la n-ième dimension ==> TOPOLOGIE,
Transcombinatoire, cube dans la n-ième dimension ==>
PRETOPOLOGIE

Conclusion
Partant
des
structures algébriques et topologiques en Théorie des Catégories,
il est intéressant d'ouvrir les structures topologiques à la
prétopologie d'Alexander Grothendieck puis de Marcel Brissaud du
groupe Belmandt et Pretopologics (issus de Fréchet 1928), pour
s'apercevoir d'une part que tout est fondé sur l'homomorphisme et la
transitivité, et d'autre part qu'il existe dans des travaux
parallèles de l'auteur depuis 1967 des notions de
« trans-combinaison » et de « prétopologie »
dès 1971, qui parle de non-transitivité et d'hétéromorphisme
voire d'andromorphisme pour introduire les textures prétopologiques
(sonores et visuelles au départ, puis généralisées) et les
texturologies quantiques prétopologiques dans une théorie des
PréCatégories hétéro et andromorphique non transitive où la
catégorie des incomplétudes (ou fermetures transitives) devient un
facteur d'émergences texturologiques propice à la recherche
d'esthétiques musicales et visuelles voire du Design du concept
multimédia par le moteur sémantique du PolyAgogic CyberSpace
Cet exposé n'étant pas topologique son incomplétude nécessite une suite et induise de nouvelles découvertes d'espaces et de nouvelles connexions entre-eux.
Références bibliographiques :
-
(Bode 49) BODE H., MOSTELLER F., TUKEY F., et WINSOR C. : The education of a Scientific Generalist. Science, 109, 553, 1949.
-
(Bourbaki 64) BOURBAKI N. : Topologie Générale. Eléments de mathématique XVI. Actualités scientifiques et industrielles. Hermann, livre III, 1964.
-
(Emptoz 83) EMPTOZ H. : Modèle prétopologique pour la reconnaissance des formes. Applications en neurophysiologie. Thèse de Doctorat Es-Sciences de l'Université Claude-Bernard, Lyon I, 1983.
-
(Gagalowicz 83) GAGALOWICZ A. : Vers un modèle de textures. Doctorat Es-Sciences, Université Paris VI, 1983.
-
(Haralick 73) HARALICK R., SHANMUGAM K., DINSTEIN I. : Texture features of images classification. Man and Cybernetics, IEEE Transaction on Systems, 6, 1973.
-
(Julesz 78) JULESZ B., CAELLI T. : On perceptual analyzers underlying visual texture discrimination. Biological Cybernetics, 28, pp 167-175, 1978.
-
(Lipschutz 65) LIPSCHUTZ S. : General Topology. Mc Graw Hill book compagny, New York, 1965.
-
(Mitchell 65) MITCHELL B. : Theory of categories. New York, Academic Press, 1965.
-
(Molnar 85) MOLNAR F., RATSIKAS D., Some aesthetical aspects of visual exploration. Third European Conference on Eye Movements, Dourdan, 1985.
-
(Pavel 81) PAVEL M. : Des formalismes en classification et en reconnaissance des formes. Troisième Congrès AFCET de Reconnaissance des formes et Intelligence Artificielle, pp 311-322, 1981.
-
(Saint-Jean 71) SAINT-JEAN P. : Notion de Topologie Générale. Rapport interne. Ecole Supérieure d'Informatique Electronique Automatique, Paris, 1971.
-
(Saint-Jean 72) SAINT-JEAN P. : Algèbre des Structures. Rapport interne. Ecole Supérieure d'Informatique Electronique Automatique, Paris, 1972.
-
(Saint-Jean 77a) SAINT-JEAN P. : Un système informatique pour l'analyse chromosomique. Rapport d'Activité. Laboratoire de Radio-Pathologie, DPr., CEA, 1977.
-
(Saint-Jean 77b) SAINT-JEAN P.: Conception d'un système informatiquede laboratoire opérationnel pour le Centre d'Etudes de Mathématique et Automatique Musicales. CNET. Diplôme d'ingénieur de l'Ecole Supérieure d'Informatique Electronique Automatique, 1977.
-
(Saint-Jean 79) SAINT-JEAN P.: Une théorie prétopologique appliquée aux traitements de forme sur ordinateur pour l'aide à la composition automatique. Colloque "l'Artiste et l'Ordinateur", Centre Culturel Suédois, 1979.
-
(Saint-Jean 86) SAINT-JEAN P., VON HAGEN V., KOPER G., PLOEM J.S. : A pretopological texture model, a multiparametric image model and a hierarchical classification method for the analysis of digitized images. Pattern Recognition in Practice, E. GELSEMA and L. KANAL, Science Publishers B.V. North Holland, pp 102-112,1986.
-
(Saint-Jean 87) SAINT-JEAN P., EMPTOZ H. : Espace de texture prétopologique et modèles de tissus complexes. Congrès de Reconnaissance des formes et Intelligence Artificielle. AFCET, INRIA, pp 219-232, 1987.
-
(Saint-Jean 89) SAINT-JEAN P. : Processus de production et d'expérimentation biologiques et médicales par l'analyse de texture prétopologique et la robotique de laboratoire. Doctorat Es-Sciences, Université de Paris-Nord, Biologie des organismes et du développement, 1989.
-
(Serra 82) SERRA J. : Image analysis and mathematical morphology. Academic Press editor, 1982.
-
(Vallée 75) VALLEE R. : Observation, decision and structures tranfers in systems theory. Progress in Cybernetics and Systems Research, HPC, Vol n°1, 1975.
-
(Vallée 78) VALLEE R. : Observation et subjectivité. IFAC workshop, Information et système, AFCET, Pergamon Press, 1978.
-
(Vallée 87) VALLEE R. : Sur la modélisation de la perception. Biologie Théorique, Edition du CNRS, Paris, 1987.
-
(Von Bertalanfy 73) VON BERTALANFFY L. : Théorie générale des systèmes. Dunod, 1973.
Webographie
Publication papier et Internet des travaux de l'auteur :
- Saint-Jean Patrick, 1967 : Les Transcombinaisons et la quatrième dimention.
http://patrick.saintjean.free.fr/phpwebgallery/index.php?/category/169
- Saint-Jean Patrick, 1971 : Notion de Topologie Générale. Rapport interne.
Ecole Supérieure d'Informatique Electronique Automatique, Paris.
http://patrick.saintjean.free.fr/phpwebgallery/index.php?/category/161
- Saint-Jean Patrick, 1972 : Algèbre des structures. Rapport interne.
Ecole Supérieure d'Informatique Electronique Automatique, Paris.
http://patrick.saintjean.free.fr/phpwebgallery/index.php?/category/170
- Saint-Jean Patrick, 1977 : Système Informatique de Laboratoire Opérationnel pour la composition musicale et visuelle, UPIC.
Mémoire d'Ingénieur de l'ESIEA.
- Saint-Jean Patrick, Von Hagen V., Jean-Claude Bisconte, 1982 : A pretopological Theory applied to image analysis with a model for analysis of texture in digitalized images.
http://patrick.saintjean.free.fr/phpwebgallery/index.php?/category/159
- Saint-Jean Patrick, 1982 : Pourquoi prétopologie et non topologie, Université de Villeurbanne.
http://patrick.saintjean.free.fr/phpwebgallery/index.php?/category/162
- Saint-Jean Patrick & all, 1982 : An automatic Device for cell cultures. La robotique de Laboratoire.
http://patrick.saintjean.free.fr/phpwebgallery/index.php?/category/165
- Saint-Jean Patrick, Von Hagen V., Koper G., Ploem J.S., 1985 : A pretopological texture model, a multiparametric image model and a hierarchical classification method for the analysis of digitized images. Pattern Recognition in Practice, E. GELSEMA and L. KANAL, Science Publishers B.V. North Holland, pp 102-112.
http://patrick.saintjean.free.fr/phpwebgallery/index.php?/category/167
- Saint-Jean Patrick, 1986 : Les sciences sensorielles de l'action créatrice, Polycopié CREATIVES APSA, Université de Paris I.
http://patrick.saintjean.free.fr/phpwebgallery/index.php?/category/163
- Saint-Jean Patrick, 1986-89 : Texture prétopologique et capteurs de virus, INSERM.
http://patrick.saintjean.free.fr/phpwebgallery/index.php?/category/157
- Saint-Jean Patrick, Emptoz H., 1987 : Espace de texture prétopologique et modèles de tissus complexes. Congrès de Reconnaissance des formes et Intelligence Artificielle. AFCET, INRIA, pp 219-232.
- Saint-Jean Patrick, 1989 : Processus de production et d'expérimentation, biologiques et médicales, par l'analyse de texture prétopologique et la robotique de laboratoire, thèse de docteur es-sciences de l'Université de Paris-Nord.
http://patrick.saintjean.free.fr/phpwebgallery/index.php?/category/154
- Saint-Jean Patrick, 1989 : Les espaces de texture prétopologique et la systémique de l'organisation.
http://patrick.saintjean.free.fr/PACS/Bibliographie/SysOrg89.html
- Saint-Jean Patrick, 1994 : Utilisation et enjeux de l'image numérique, Perspectives à court et moyen terme.
PERCEPTION 3D APTEP, CNAM, Paris 1994, organisé et édité par l'Association des Professeurs de Technologie de l'Enseignement Public.
http://patrick.saintjean.free.fr/PACS/Bibliographie/CNAM94.html
- Saint-Jean Patrick, 1997 : To a behavioural Design, an other perspective for the 3D perspective of image synthesis to be immerse in new virtual worlds and to settle in its proper live. ACM-Siggraph Education.
http://patrick.saintjean.free.fr/PACS/Bibliographie/ComputGraph97.html
- Saint-Jean Patrick, 1997 : The PolyAgogic CyberSpace Project. A multimedia system for texturing, networking, and practising knowledge. Edugraphics'97, Computer Graphics'97 Third International Conference on Graphics Education, Vilamoura, Algarve, Portugal. Edited by GRASP - Graphic Science Promotions & Publications. ISBN 972-8342-02-0.
http://patrick.saintjean.free.fr/PACS/Bibliographie/Edugraphics97.html
- Saint-Jean Patrick, 1998 : PolyAgogic CyberSpace VOLUNTAry Textured and Integrated System. Cyber Espace PolyAgogique comme système d'information volontairement texturé et intégré par le multimédia en réseau local et global pour l'enseignement par la création et la culture. Proposition au Programme européen ESPRIT.
http://patrick.saintjean.free.fr/PACS/Bibliographie/ProgESPRIT98.html
- Saint-Jean Patrick, 1999 : PROPOSALS of an European Digital Interactive Spaces Network EDISN. PROPOSAL NUMBER : IST - 1999 - 11373 25/5/99. The Fifth Framework Program focuses on Community activities in the field of research, technological development and demonstration (RTD) for the period 1998 to 2002. European Commission.
http://patrick.saintjean.free.fr/PACS/Bibliographie/EDISNETIST99.html
- Saint-Jean Patrick, 1999 : PolyAgogic CyberSpace IMAGINA Monaco 1999.
http://patrick.saintjean.free.fr/PACS/Bibliographie/IMAGINAMonaco99.html
- Saint-Jean Patrick, 2000 : Les Cyber-Espaces Polyagogiques et l'Univers Cités Virtuelles Interactives pour l'accès au patrimoine culturel et scientifique, l'éducation et la création artistique multimédia et audiovisuelle en réseau. IMAGINA 2000.
http://patrick.saintjean.free.fr/PACS/Bibliographie/UCVIV2000.html
- Saint-Jean Patrick, 2000 : The PolyAgogic CyberSpaces and the Design of the multimedia concept for the networked cultural and scientific inheritance, education, multimedia and audiovisual artistic creation access. Proceeding, Laval Virtual, Virtual Reality International Conferences 2000, Laval the 18-21 May 2000.
http://patrick.saintjean.free.fr/PACS/Bibliographie/LavalVirtual2000/PSJLV2000.html
http://patrick.saintjean.free.fr/PACS/Bibliographie/LavalVirtual2000/Conceptatrium.html
- Patrick Saint-Jean 2001 : « Univers, Cités Virtuelles Interactives (U.C.V.I.) : Le Design du Concept Multimédia en Cyber-Espace pour l'accès au patrimoine culturel et scientifique en réseau, la création multimédia, la polyagogie et le spectacle interactif de la connaissance », ASTI'2001, Sciences et Technologies de l'Information. A la Cité des Sciences et de l'Industrie, Paris La Villette.
http://acmsiggraphparispc.free.fr/P0/PRASTI2001.html
- Patrick Saint-Jean 2003 : « Loin d'être hors contrôle, le concept de cybernétique se régule en France dans un domaine non centralisé mais distribué en réseau : Information, Systémique et Cybernétique ». Cybernetics in the Third Millennium (C3M) e-Zine archive (vol. 2.3, 2.5, March and May 2003).
http://www.well.com/~abs/Cyb/4.669211660910299067185320382047/c3m_0205.txt
http://paris.siggraph.org/CyberFR/CybernetiqueSommaire.html
- Patrick Saint-Jean 2004 : Vers une texturologie quantique. Séminaire ESIEA.
http://patrick.saintjean.free.fr/PACS/Bibliographie/TQ2004/TQ.html
- Patrick Saint-Jean 2005 : La Cybernétique, l'Art cybernétique et l'ère cyber. Festival du Jubilé de l'Art Cybernétique, Atelier Schöffer.
http://acmsiggraphparispc.free.fr/SIGGRAPH2005/PSJCACEC.html
- Patrick Saint-Jean 2005 : Le futur de l'intelligence artificielle. ASTI'2005,Clermond-Ferrand.
http://patrick.saintjean.free.fr/PACS/Bibliographie/FAI/PSJASTI05FAI.html
- Patrick Saint-Jean 2006 : Prétopologie et texturologie quantique : Une aventure Texturologique Quantique pour une interactivité, intercréativité et intercréactivité humaines. 69 ème Rencontre du Groupe de travail Voir et produire des images d'art et de science, Université PARIS-SUD.
http://acmsiggraphparispc.free.fr/SIGGRAPH2006/TQ2006/TQ2006.html
- Patrick Saint-Jean 2006 : Le PolyAgogic CyberSpace et l'Intelligence Artificielle. En l'honneur du cinquantenaire de l'Intelligence artificielle.
Ministère de la Recherche, 1 rue Descartes, Paris. http://patrick.saintjean.free.fr/PACS/Bibliographie/PACSIA/ProjetPACSIA.html
- Patrick Saint-Jean 2007 : Sculpture du concept et texturologie quantique. Intersculpt 2007, Ars Mathématica, ENSAM.
http://patrick.saintjean.free.fr/PACS/Bibliographie/InterSculpt2007/ConferencePSJIntersculpt2007.html
http://patrick.saintjean.free.fr/PACS/Bibliographie/InterSculpt2007/PosterPSJIntersculpt2007.jpg
- Patrick Saint-Jean 2009 : Le projet du PolyAgogic CyberSpace : La sculpture de la connaissance par le Design du Concept multimédia.
Les Texturologies quantiques et la sculpture du quanta informationnel dans l'espace CyberAgogique pour l'apprentissage, la création et le spectacle de la connaissance. Intersculpt 2009, Fête de la Science 2009 en Lorraine, Ars Mathématica.
http://patrick.saintjean.free.fr/PACS/Bibliographie/InterSculpt2009/ConferencePSJIntersculpt2009.html
- Patrick Saint-Jean 2010 : De la prétopologie dans les texturologies quantiques et la topologie augmentée. 7-ième Journée de la Prétopologie Université de Versailles Saint-Quentin.
http://patrick.saintjean.free.fr/PretopologieTQTAPSJ.html
- Patrick Saint-Jean 2010 : Panorama, enjeux et provocations du Bio-Art. Overview, challenges and provocations of BioArt. Entre le Molécule-Art et le Body-Art : le Bio-Art. Fête de la Science 2010, Ars Mathématica, Cyberbase, Carrefour Numérique, Médiathèque, Bibliothèque, Cité des Sciences et de l'Industrie, Universcience.
http://patrick.saintjean.free.fr/FdSAMCBUniverscience2010/PEPduBioArtPSJAM2010.html
http://patrick.saintjean.free.fr/FdSAMCBUniverscience2010/PosterPSJFdSAMCSI2010.html
Autres bibliographies intéressantes et utiles :
- ZT. Belmandt 2011 : Basics of pretopology, Hermann éditeur.
- Edouard Glissant 2010 : Philosophie de la relation, poésie en étendue, Gallimard éditeur.
- Marc Bui, Ivan Lavallée 2009 : Prétopologie et modélisation, Vol. 7.1, Hermann Editeurs des sciences et des arts.
- Robert Martin 2001 : Sémantique et automate, Ecriture électroniques, PUF éditeur.
- Claude Hagège 1996 : L'homme de paroles, Contribution linguistique aux sciences humaines, Le temps des sciences, Fayard éditeur.
- Robert Vallée 1995 : Cognition et Système,essai d'Epistémo-Praxéologie, l'Interdisciplinaire, Système(s) éditeur.
- Eveline Martin 1993 : Reconnaissance de contextes thématiques dans un corpus textuel. Elements de lexico-sémantique. Collection "Etudes de sémantique lexicale". CNRS INaLF-Nancy, Directeur : Robert Martin. Didier Erudition éditeur, Paris.
- Z. Belmandt 1993 : Manuel de prétopologie et ses applications, Interdisciplinarité et nouveaux outils, Hermes éditeur.
- Haïm Nisenbaum 1989 : Texture hébraïque, L'Aire Libre Edition, Collection "Quintessence".
- Michel Thévoz 1986 : Duduffet, Skira Editeur.
- Michel de Certeau 1980 : L'invention du quotidien 1. arts de faire, Chapître VII Marche dans la ville, page 139-141, Gallimard Editeur (Nouvelle édition 1990 par Luce Giard).
- Michel de Certeau 1969 : L'étranger ou l'union dans la différence, Du Seuil Editeur (Nouvelle édition 2005 par Luce Giard).